基于切比雪夫空间距离的空间跳跃体绘制加速方法(Empty Space Skipping-ESS)

转载请注明出处（￣︶￣）↗https://blog.csdn.net/surpass2019/article/details/103789360
转载请注明出处（￣︶￣）↗
转载请注明出处（￣︶￣）↗

开学前老板就分了体绘制的方向，在知道了基础的光线投射算法（一种经典的体绘制方法）后，我开始寻找速度更快的体绘制方法，来提高渲染的帧率。经典的光线投射算法如果以后有时间，我就详细记录一下，这次来认真梳理一下一种加速体绘制的方法——基于切比雪夫空间距离的空间跳跃体绘制算法。
很惭愧，我的学习和理解能力不咋地，有不对的地方希望大佬指出来，一起讨论！一起进步~

常见的加速方法

今天分享的这篇论文是基于光线投射算法的，而体绘制（将三维立体的内部信息呈现在最后的二维纹理中）这一领域，实现绘制的算法除了光线投射算法，还有其他的方法，比如最大强度投影算法，抛雪球法（足迹表法），剪切曲变法（在CPU上速度最快的体绘制方法？）等等，不同的体绘制方法都有基于这种方法的加速手段，于是这些加速算法今天都不考虑==，提供一些搜索的关键字咯：早期光线终止（Early Ray Termination），八叉树，BSP空间分割，自适应多分辨率，预积分体绘制，图形硬件加速等方法…
其实加速的一个关键思想就是尽量减少不必要的体素渲染数量，很多加速方法都殊途同归。

空间跳跃加速方法ESS

基于光线投射算法，想要尽量减少不必要的体素渲染数量，那就把那些空体块跳过呗，怎么跳过？先把一个大的初始三维图形分块，再将每个块标记上0-1值（0代表empty/1代表occupied），再计算并记录每个块与相离最近的块的距离，然后再最后的光线投射算法中根据记录的距离值判断跳过多少空体块，最后渲染。基于切比雪夫距离的空间跳跃加速方法(Empty Space Skipping-ESS)基本思想就是这样。
先附上本文要详细解说的论文，今年Sigraph Asia里的一篇：
accelerated volume rendering with chebyshev distance maps
预探详情，请搭梯子。

这篇论文新鲜出炉，并且分量十足，登在Sigraph Asia 2019，并且论文还在github上附有源码，于是今天把最重要的计算着色器的内容拿出来分析一下，希望理解了计算着色器里计算occupancy_map和distance_map的思想，就可以动手在其他工程里用到这种加速方法了。

ESS基本思想

大体的思路就是，给一个初始Volume，其3个维度为[width,height,depth]，将初始Volume分块，每个块的大小为block_size（表示一个block中包含的体素个数），想象一下一个大的正方体变成小些的正方体，大的正方体存储width* height* depth个体素，而小的正方体里存储(width/block_size) * (height/block_size)* (depth/block_size)个体素，小的正方体就叫做occupancy_map,这个occupancy_map里只记录0-1值，就将原Volume分块了，表示这个Volume的这么多部分中，哪一块是非空的，哪一部分是空的。我们只想渲染那些非空的部分，这时候需要一个和occupancy_map一样大的distance_map，用来记录该体块到距离最近的非空体块的切比雪夫距离。(分别计算对比三个轴方向xoy,xoz,yoz的最短距离)

切比雪夫距离：在向量中，表示两个向量中各个坐标分量差值绝对值的最大值
比如：（2,3,4）(5,7,8)的切比雪夫距离就是5，因为（|5-2|，|7-3|，|9-4|）=（3,4,5）

总之，这篇论文可以分为三个部分：

• 计算生成occupancy_map
• 计算生成distance_map
• 根据distance_map进行基于光线投射算法的渲染

计算生成occupancy_map

原始的体数据三个维度分别为：（当然这也可以当做坐标）

标准化坐标为

一条射线上的n个采样点，计算n的公式为：

不难思考得到，f表示每单位距离之间delta_t的个数，所以f大于等于1。下面的式子计算标准采样间隔：

若想用标准化坐标计算第i个采样点的坐标，就这样：

以上就是进行光线投射算法所需用到的一些变量。在这里介绍的论文中，采用基于切比雪夫距离的空间跳跃算法，还需要理解block的概念，如何跳过这些block？先需要知道以下变量：
B是block的大小，t_M表示在distance_map或occupancy_map的标准化坐标。

细心观察这个图：
就是先理解这里二维block的概念，然后延伸到三维空间中去想象。小的正方形就是blocks，一个大的体数据会被分为d/B（这里是向量）个block，每个block都会用occupancy_map记录是否含有不透明的体素。假设光线采样到u_M处，会跳过两个成分：1.当前block的剩余部分2.空的体块，然后到达下一个非空体块的第一个采样点处，再开始进行光线投射。接下来所有的公式都建立在对这个图的理解上。

计算生成distance_map

重点是如何生成distance_map，这篇论文用的方法没有详细说，在另外一篇论文里介绍了。Saito和Toriwaki发在1994年CVPR上的一篇经典文章，自行搭梯获得，不过本文将经典的欧几里得距离换成了切比雪夫距离。下面的公式是用在光线投射算法的ESS中。在下面这个公式中，重点观察delta大于0的时候，有助于理解。delta小于0的时候也不难理解，采用小数减大数为负，就可以和除数的符号抵消，最后求得步长（正数）。（也就是说经过delta_i_j的步数后可以到达下一个block的第一个采样点，其中j属于{x,y,z}三个轴符号的集合）这个公式的基础是上面那个图，用于计算block中剩余的采样步数：

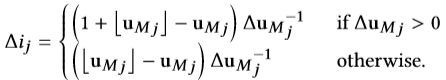
再将三个坐标分量的delta值进行如下的操作——取三个分量值的最小值，并且圆整，其中step()是阶跃函数，表示如果delta_um为负取0，delta_um为正取1（就是对上面式子分类讨论的两种情况的归一式），最后的delta_i用于计算图中u_M到达下一个block的切比雪夫距离，最后步数公式如下：

以上是计算跳过一个block剩余部分的公式，而实际上，我们要计算的是跳过的两个部分的切比雪夫距离，对于第2部分（1.当前block的剩余部分2.空的体块） 。切比雪夫距离如何计算呢？

至于为什么要用切比雪夫距离，作者说这样可以使得一次跳过很多个块，就不用一个一个跳了？还要理解，对于distance_map，是用切比雪夫距离进行填充的。与计算剩余block距离相似，如果要计算跳过D个blocks，所需的步数公式如下：

上面这个公式依然关注的是delta大于0的部分。这样一来就会跳过D个体块。下面这个公式中delta_i代表的就是最终跳过D个体块所需的步数：

代码分析

计算着色器语法

occupancy_map.comp

下面是论文作者放在github上的源码，戳我戳我><,我试着分析一下这个计算着色器。
首先是occupancy_map.comp，注意一下调用计算着色器的次数与block的个数（也就是occupancy_map的三个维度之积相同）

#version 460
//局部工作组的大小为512，说明512个对计算着色器的调用可以并行
//512个block并行赋值
layout (local_size_x = 8, local_size_y = 8, local_size_z = 8) in;
layout (set = 0, binding = 0, r8) uniform image3D volume; // r8 = float unorm
#ifdef PRECOMPUTED_GRADIENT
layout (set = 0, binding = 1, r8) uniform image3D gradient;
#endif
#ifdef TRANSFER_FUNCTION_TEXTURE
layout (set = 0, binding = 2) uniform sampler2D transfer_function;  // transfer function (rgba)
#endif
layout (set = 0, binding = 3, r8ui) uniform uimage3D occupancy_map;

layout(push_constant) uniform PushConsts {
    vec4 block_size;
    float grad_magnitude_modifier;
#ifndef TRANSFER_FUNCTION_TEXTURE
    float intensity_min;
    float intensity_max;
    float gradient_min;
    float gradient_max;
#endif
};

const uint OCCUPIED = 0;
const uint EMPTY = 1;

void main() {
  const ivec3 dimDst = imageSize(occupancy_map);
  if(any(greaterThanEqual(gl_GlobalInvocationID, dimDst))) return;
  //

  const ivec3 dimSrc = imageSize(volume);

  const ivec3 start = ivec3(gl_GlobalInvocationID * block_size.xyz);
  ivec3 end = ivec3(min(dimSrc, start + block_size.xyz));
  //处理block的维度小于规定维度的情况
  end.x = (dimSrc.x - end.x) < block_size.x ? dimSrc.x : end.x;
  end.y = (dimSrc.y - end.y) < block_size.y ? dimSrc.y : end.y;
  end.z = (dimSrc.z - end.z) < block_size.z ? dimSrc.z : end.z;
  
#ifndef TRANSFER_FUNCTION_TEXTURE
  float intensity_range_inv = 1.0f / (intensity_max - intensity_min); 
  float gradient_range_inv = 1.0f / (gradient_max - gradient_min);
#endif
//calculate theh occupency_map which only contains the intensity
//Volume中每个体素都要遍历
  ivec3 pos;
  for (pos.z = start.z; pos.z < end.z; ++pos.z)
    for (pos.y = start.y; pos.y < end.y; ++pos.y)
      for (pos.x = start.x; pos.x < end.x; ++pos.x) {
        // Intensity
        float intensity = imageLoad(volume, pos).x;

#ifdef PRECOMPUTED_GRADIENT
        // Gradient from precomputed texture
        float gradient = imageLoad(gradient, pos).x;
#else
        // Gradient on-the-fly using tetrahedron technique http://iquilezles.org/www/articles/normalsSDF/normalsSDF.htm
        ivec2 k = ivec2(1,-1);
        vec3 gradientDir = (k.xyy * imageLoad(volume, clamp(pos + k.xyy, ivec3(0), ivec3(dimSrc)-1)).x +
                            k.yyx * imageLoad(volume, clamp(pos + k.yyx, ivec3(0), ivec3(dimSrc)-1)).x +
                            k.yxy * imageLoad(volume, clamp(pos + k.yxy, ivec3(0), ivec3(dimSrc)-1)).x +
                            k.xxx * imageLoad(volume, clamp(pos + k.xxx, ivec3(0), ivec3(dimSrc)-1)).x) * 0.25f;
        float gradient = clamp(length(gradientDir) * grad_magnitude_modifier, 0, 1);
#endif

#ifdef TRANSFER_FUNCTION_TEXTURE
        // Get alpha from transfer function texture
        float alpha = textureLod(transfer_function, vec2(intensity, gradient), 0.0f).a;

#else
        // Get alpha from simple grayscale transfer function
        float alphaIntensity = clamp((intensity - intensity_min) * intensity_range_inv, 0, 1);
        float alphaGradient= clamp((gradient - gradient_min) * gradient_range_inv, 0, 1);
        float alpha = alphaIntensity * alphaGradient;
#endif
//只要block中存在一个体素含有意义，那么这个block就赋值为1
        if (alpha > 0.0f) {
          // Set region as occupied
          imageStore(occupancy_map, ivec3(gl_GlobalInvocationID), ivec4(OCCUPIED));
          return;
        }
      }

  // Set region as empty
  imageStore(occupancy_map, ivec3(gl_GlobalInvocationID), ivec4(EMPTY));
}

distance_map.comp

下面放上distance_map的计算着色器源码，依然来自上文所附的github连接。distance_map的大小和occupancy_map大小一致

• dist_swap是中间计算量
• dist保存最后的切比雪夫值
• 看不懂的同学看下这篇文章：Saito和Toriwaki发在1994年CVPR上的一篇经典文章，关于欧几里得距离转换

#version 460
//设置了局部工作组的大小为8X8
//这个计算着色器的计算单元以面为单位，而不是以三维立体为计算单位
layout (local_size_x = 8, local_size_y = 8) in;

layout (binding = 0, r8ui) uniform uimage3D dist;
layout (binding = 1, r8ui) uniform uimage3D dist_swap; // occupancy_map on stage 0

layout(push_constant, std430) uniform PushConsts { 
    uint stage;
};

// Based on [Saito and Toriwaki, 1994]
//    "New algorithms for euclidean distance transformation of an n-dimensional digitized picture with applications"
//    with modifications:
//      * runs on a GPU, uses a 3D swap image rather than a 1D buffer
//      * compute Chebyshev distance rather than Euclidean distance
//      * specific optimisations related to Chebyshev/GPU and sample reduction

// call as:
//  pushConsts(0)
//  dispatch(rndUp(height, 8), rndUp(depth, 8));
//  pushConsts(1)
//  dispatch(rndUp(width, 8), rndUp(depth, 8));
//  pushConsts(2)
//  dispatch(rndUp(width, 8), rndUp(height, 8));

const uint OCCUPIED = 0;
const uint EMPTY = 1;

//对occupancy_map里的值进行魔改咯，block为空就把距离填到最远处，block非空distance_map距离就填0
uint occupancy_to_max_dist(uint occupancy) {
  return occupancy == OCCUPIED ? 0 : 255;
}

void main() {
    ivec3 pos;
    if (stage == 0) {
    //阶段一：从occupancy_map转化成x方向的切比雪夫最短距离
      pos = ivec3(0, gl_GlobalInvocationID.x, gl_GlobalInvocationID.y);
    } else if (stage == 1) {
    //阶段二：对比x方向的距离和y方向的距离，再确定最小值
      pos = ivec3(gl_GlobalInvocationID.x, 0, gl_GlobalInvocationID.y);
    } else {
    //阶段三：对比刚刚得到的x或y轴的最小距离与z方向的距离，再确定最终的distance_map
      pos = ivec3(gl_GlobalInvocationID.x, gl_GlobalInvocationID.y, 0);
    }

    const ivec3 dim = imageSize(dist);
    if(any(greaterThanEqual(pos, dim))) return;

    if (stage == 0) { // "Transformation 1"
        // Forward
        uint gi1jk = occupancy_to_max_dist(imageLoad(dist_swap, ivec3(0, pos.y, pos.z)).x);
        for (int x = 0; x < dim.x; ++x) {
          ivec3 p = ivec3(x, pos.y, pos.z);
		  //把x轴方向的像素遍历一边，存储在distance_map中（8*8个工作项同步工作）
		  //非空就是0，空就骗到255
          uint gijk = occupancy_to_max_dist(imageLoad(dist_swap, p).x);//从dist_swap取
          uint gijk_new = min(gi1jk + 1, gijk);
                   
          imageStore(dist, p, ivec4(gijk_new)); //存在dist中
          gi1jk = gijk_new;
        }

        // Backward
        gi1jk = imageLoad(dist, ivec3(dim.x - 1, pos.y, pos.z)).x;
        for (int x = dim.x - 2; x >= 0; --x) {
          ivec3 p = ivec3(x, pos.y, pos.z);
          uint gijk = imageLoad(dist, p).x;//从dist取
          uint gijk_new = min(gi1jk + 1, gijk);
          
          imageStore(dist, p, ivec4(gijk_new));//存在dist中
          gi1jk = gijk_new;
        }
    } else if (stage == 1) { // "Transformation 2"
        for (int y = 0; y < dim.y; ++y) {
          ivec3 p = ivec3(pos.x, y, pos.z);
          uint gijk = imageLoad(dist, p).x;
          uint m_min = gijk;
          // zigzag out from the voxel of interest, stop as soon as any future voxels
          // are guaranteed to return a higher distance
          for (int n = 1; n < m_min && n < 255; ++n) {
            if (y >= n) {
              const uint gijnk = imageLoad(dist, ivec3(pos.x, y - n, pos.z)).x;//从dist取
              const uint m = max(n, gijnk);
              if (m < m_min)
                m_min = m;
            }
            if ((y + n) < dim.y && n < m_min) { // note early exit possible
              const uint gijnk = imageLoad(dist, ivec3(pos.x, y + n, pos.z)).x;//从dist取
              const uint m = max(n, gijnk);
              if (m < m_min)
                m_min = m;
            }
          }
          imageStore(dist_swap, p, ivec4(m_min));//存在dist_swap中,方便下面取
        }
    } else if (stage == 2) { // "Transformation 3"
        // same as transformation 2 but on the z axis
        for (int z = 0; z < dim.z; ++z) {
          ivec3 p = ivec3(pos.x, pos.y, z);
          uint gijk = imageLoad(dist_swap, p).x;
          uint m_min = gijk;
          for (int n = 1; n < m_min && n < 255; ++n) {
            if (z >= n) {
              const uint gijnk = imageLoad(dist_swap, ivec3(pos.x, pos.y, z - n)).x;//从dist_swap取
              const uint m = max(n, gijnk);
              if (m < m_min)
                m_min = m;
            }
            if ((z + n) < dim.z && n < m_min) { // note early exit possible
              const uint gijnk = imageLoad(dist_swap, ivec3(pos.x, pos.y, z + n)).x;//从dist_swap取
              const uint m = max(n, gijnk);
              if (m < m_min)
                m_min = m;
            }
          }
          imageStore(dist, p, ivec4(m_min));//存在dist中，就是最终的distance_map
        }
    }
}