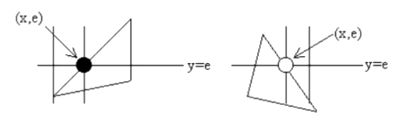
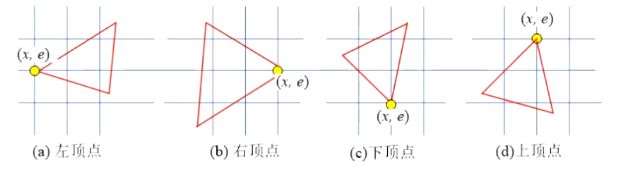
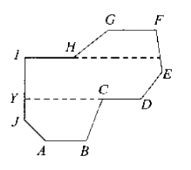
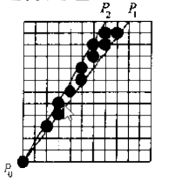
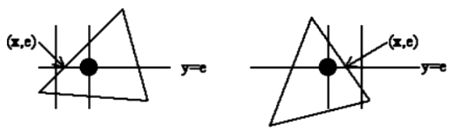二维填充图元的生成
文章目录
- 二维填充图元的生成
- 1. 扫描转换矩形
- 2. 扫描转换多边形
- 2.1 多边形的表示方法
- 2.1.1 顶点表示
- 2.2.2 点阵表示
- 2.2 多边形的扫描转换
- 2.3 扫描转换方法：
- 2.3.1 逐点判断法
- 2.3.1.1 射线法
- 2.3.1.2 累计角度法
- 2.3.1.3 编码方法
- 2.3.2 扫描线算法
- 2.3.2.1 区域连贯性
- 2.3.2.2 扫描线的连贯性
- 2.3.2.3 边的连贯性
- 2.3.2.4 算法
- 2.3.2.5 数据结构
- 2.3.2.6 算法实现
- 2.3.2.7 算法特点
- 3. 区域填充
- 3.1 区域的表示方法
- 3.2 区域的类型
- 3.3 递归填充算法
- 3.3.1 内点表示4连通区域的递归填充算法
- 3.3.2 扫描线填充算法
- 3.3.2.1 算法举例
- 3.3.2.2 算法特点
- 4. 多边形扫描转换与区域填充比较
二维填充图元的生成
填充图元的扫描转换步骤
多边形扫描转换与区域填充可以统称为区域填充，就是如何用颜色或图案来填充一个二维区域。填充主要做两件工作：
- 确定哪些像素位于填充图元的内部；
- 确定以什么颜色/图案填充这些像素。
1. 扫描转换矩形
问题：
- 矩形是简单的多边形，为什么要单独处理矩形？
相比一般多边形扫描算法来讲，可简化计算、提高效率。应用非常多，窗口系统。 - 共享边界如何处理
原则：左闭右开，下闭上开。
typedef struct {int xmin, xmax, ymin, ymax;
} Rectangle; // 定义一个矩形结构体
void FillRectangle(Rectangle *rect, int color) {
int x, y;
for (y = rect->ymin; y <= rect->ymax; y++) {
for (x = rect->xmin; x <= rect->xmax; x++) {
PutPixel(x, y, color); // 像素点填充颜色
}
}
}
2. 扫描转换多边形
多边形分为凸多边形、凹多边形、含内环的多边形。
2.1 多边形的表示方法
2.1.1 顶点表示
用多边形顶点的序列来刻画多边形。直观、几何意义强、占内存少；不能直接用于面着色。
2.2.2 点阵表示
用位于多边形内的像素的集合来刻画多边形。 失去了许多重要的几何信息；便于运用帧缓冲存储器表示图形，易于面着色。
2.2 多边形的扫描转换
把多边形的顶点表示转换为点阵表示，也就是从多边形的给定边界出发，求位于其内的各个像素，并给帧缓冲器内的各个对应元素设置相应的灰度和颜色，通常称这种转换为多边形的扫描转换。
2.3 扫描转换方法：
2.3.1 逐点判断法
逐点判断的算法虽然程序简单，但不可取。原因是速度太慢，主要是由于算法割断了各像素之间的联系，孤立地考察各像素与多边形的内外关系，使得几十万甚至几百万个像素都要一一判别，每次判别又要多次求交点，需要做大量的乘除运算，花费很多时间。
#define MAX 100
typedef struct {
int PolygonNum; // 多边形顶点的个数
Point vertexces[MAX]; // 多边形顶点数组
} Polygon
void FillPolygonPbyP(Polygon *P, int polygonColor) {
int x, y;
for (y = ymin; y <= ymax; y++)
for (x = xmin; x <= xmax; x++)
if (IsInside(P, x, y)) // 判断像素点是否在多边形内部
PutPixel(x, y, PolygonColor);
else
PutPixel(x, y, backgroundColor);
} // end of FillPolyPbyP()
- 逐个判断绘图窗口内的像素。
- 如何判断点在多边形的内外关系？
- 射线法
- 累计角度法
- 编码法
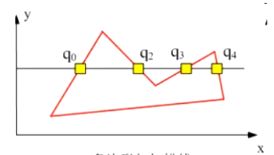
2.3.1.1 射线法
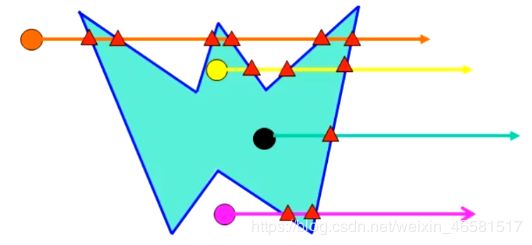
从此点出发，向左或向右做射线，如果射线和多边形交点数为奇数，则这一点在多边形区域内，否则在多边形区域外。
2.3.1.2 累计角度法
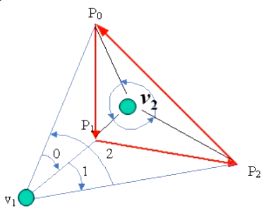
- 从 v v v点向多边形 P P P顶点发出射线，形成有向角 θ i = ∠ P i v P i + 1 。 \theta_i = \angle P_ivP_{i+1}。 θi=∠PivPi+1。（大小计算可用余弦定理）
- 计算有向角的和，得出结论：
∑ i = 0 n θ i = { 0 , v 位 于 P 之 外 ± 2 π , v 位 于 P 之 内 \sum\limits_{i = 0}^n\theta_i = \begin{cases} 0, \ \qquad v位于P之外 \\ \pm2\pi, \quad v位于P之内 \end{cases} i=0∑nθi={0, v位于P之外±2π,v位于P之内
2.3.1.3 编码方法
- 预处理，测试点是否在边上；
- 以 V V V为原点作局部坐标系，对其象限按逆时针（或顺时针）编码；
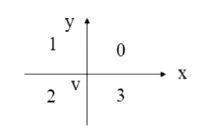
- 对多边形的顶点进行编码， I p i Ip_i Ipi（等于象限编号）；
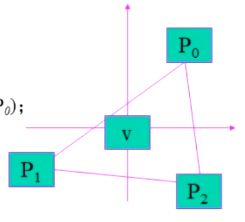
- 对多边形的边进行编码：
△ P i P i + 1 = I p i + 1 − I p i \triangle P_iP_{i+1} = Ip_{i+1} - Ip_i △PiPi+1=Ipi+1−Ipi； - 计算 ∑ △ P i P i + 1 \sum{\triangle P_iP_{i+1}} ∑△PiPi+1（其中 △ P n P n + 1 = △ P n P 0 \triangle P_nP_{n+1} = \triangle P_nP_0 △PnPn+1=△PnP0）；
Note：要求 △ P i P i + 1 \triangle P_i P_{i+1} △PiPi+1的绝对值不大于2
处理方法：- 当 △ P i P i + 1 = 3 \triangle P_i P_{i+1} = 3 △PiPi+1=3时，令 △ P i P i + 1 = △ P i P i + 1 − 4 = 1 \triangle P_i P_{i+1} = \triangle P_iP_{i+1} - 4 = 1 △PiPi+1=△PiPi+1−4=1
- 当 △ P i P i + 1 = − 3 \triangle P_i P_{i+1} = -3 △PiPi+1=−3时，令 △ P i P i + 1 = △ P i P i + 1 + 4 = 1 \triangle P_i P_{i+1} = \triangle P_i P_{i+1} +4 = 1 △PiPi+1=△PiPi+1+4=1
- 若 ∑ △ P i P i + 1 = 0 ， V \sum \triangle P_i P_{i+1} = 0， V ∑△PiPi+1=0，V在 P P P外；
- 若 ∑ △ P i P i + 1 = ± 4 \sum \triangle P_i P_{i+1} = \pm4 ∑△PiPi+1=±4, V V V在 P P P内。
2.3.2 扫描线算法
扫描线算法是多边形扫描转换的常用算法。与逐点判断算法相比，扫描算法充分利用了相邻像素之间的连贯性，避免了对像素的逐点判断和反复求交的运算，达到了减少计算量和提高速度的目的。
开发和利用相邻像素之间的连贯性是光栅图形算法研究的重要内容。扫描线算法综合利用了区域的连贯性、扫描线连贯性和边的连贯性等三种形式的连贯性。
2.3.2.1 区域连贯性
区域的连贯性是指多边形定义的区域内部相邻的像素具有相同的性质。例如具有相同的颜色。
- 两条扫描线之间的长方形区域被所处理的多边形分割成若干梯形（三角形可以看作退化的梯形）；
- 梯形的底边为扫描线，梯形的腰为多边形的边或窗口边缘；
- 梯形分为两类：一类在多边形内部，一类在多边形外部，两类梯形在长方形区域相间排列。
推论：如果长方形区域内任一梯形内一点关于多边形 P P P的 内外关系确定后，即可确定区域内所有梯形关于 P P P的内外关系。
效率高的根源：逐点判断——>区域判断
2.3.2.2 扫描线的连贯性
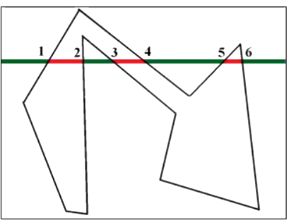
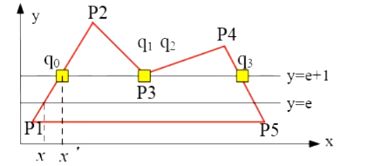
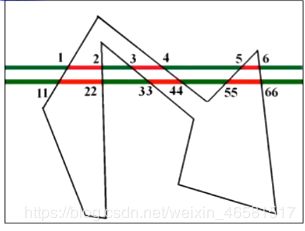
- 交点序列：扫描线与多边形的交点个数为偶数 ( 1 , 2 , 3 , 4 , 5 , 6 ) (1,2,3,4,5,6) (1,2,3,4,5,6)。
- 红色区间 ( 1 , 2 ) 、 ( 3 , 4 ) 、 ( 5 , 6 ) (1,2)、(3,4)、(5,6) (1,2)、(3,4)、(5,6)位于多边形内部。
- 绿色区间位于多边形外部。
推论：如果上述交点区间属于多边形内（外），那么该区间内所有点均属于多边形内（外）。
逐点判断——>区间判断
2.3.2.3 边的连贯性
相邻扫描线 ( y 1 = y 11 + 1 ) (y_1 = y_{11}+1) (y1=y11+1)与多边形的同一条边的交点存在如下关系： y 1 − y 11 x 1 − x 11 = k x 1 = x 11 + 1 k \frac{y_1 - y_{11}}{x_1 - x_{11}} = k \\ \\ x_1 = x_{11} + \frac{1}{k} x1−x11y1−y11=kx1=x11+k1
当知道扫描线与一条边的一个交点之后，通过上述公式可以通过增量算法求出其他交点
推论：边的连贯性是区域连贯性和扫描线连贯性的纽带。
扫描线连惯性“+”边连贯性“=”区域连贯性
2.3.2.4 算法
- 目标：利用相邻像素之间的连贯性，提高算法效率；
- 处理对象：非自交多边形（便于边之间除了顶点外无其它交点）。
- 扫描转换步骤——对于每一条扫描线：
- 求交点；
- 交点排序；
- 交点配对；
- 填充区段；
- 求交点
- 要求：生成的像素全部位于多边形之内
- 求交方法：
扫描转换直线算法采用四舍五入原则易导致部分像素位于多边形之外，从而需要改进。
第一类边：与 y = e y=e y=e和 y = e + 1 y = e+1 y=e+1同时相交，则新交点的横坐标为： x ′ = x + 1 k x' = x+\frac{1}{k} x′=x+k1
第二类边：只与 y = e + 1 y = e+1 y=e+1相交，则新交点的横坐标为该边的下断点。 - 交点取整规则：
- X为小数，即交点落在扫描线上两个相邻像素之间。
- 交点位于左边上，向右取整
- 交点位于右边上，向左取整
- 边界上的像素的取舍问题，避免填充扩大化
- 边界像素：规定落在右上边界的像素不予填充。
- 具体实现时，只要对扫描线与多边形的相交区间左闭右开。
- 扫描线与多边形的顶点相交时，交点的取舍，保证交点正确配对
+ 下闭上开 - 特殊情况处理
- 水平边：在算法预处理阶段将它们去掉。
- 尖角：应通过反混淆算法进行处理。
- 水平边：在算法预处理阶段将它们去掉。
- X为小数，即交点落在扫描线上两个相邻像素之间。
2.3.2.5 数据结构
扫描线算法的数据结构由边的分类表（Edge Table， ET）和活化边表（Active Edge List，AEL）两部分组成。两个表结构中基本元素是边结构。
边结构定义：
typedef struct {
int ymax; // 边的上端点的y坐标
float x, deltax; // deltax为边的斜率的倒数
struct Edge *nextEdge; // 指向下一条边的指针
} Edge
- 边的分类表ET：
是按边的下端点的y坐标对非水平边进行分类的指针数组。下端点的y坐标值等于i的边归入第i类。有多少条扫描线，就设多少类。同一类中，各边按x值（x值相等时，按 Δ x \Delta x Δx的值）递增顺序排列成行。
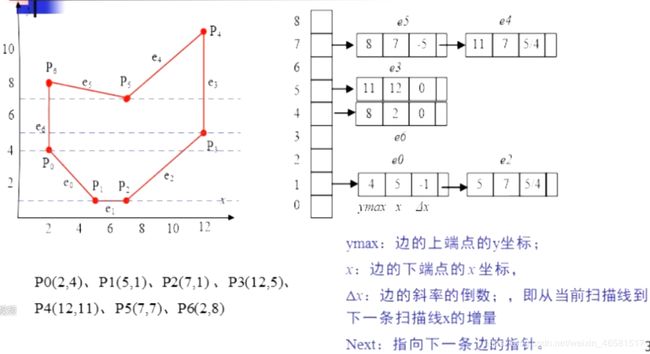
作用：边的分类表的作用是避免盲目求交。当处理一条扫描线时，为了求出它与多边形的所有交点，必须将它与所有的边进行求交测试。而实际上只有某几条边与该扫描线有交点。边的分类表正是用来排除不必要的求交测试。 - 活化边表AEL：
活化边表由与当前扫描线相交的边组成，记录多边形的边和当前扫描线的所有交点的x坐标，并随扫描线的递增而不断变化。
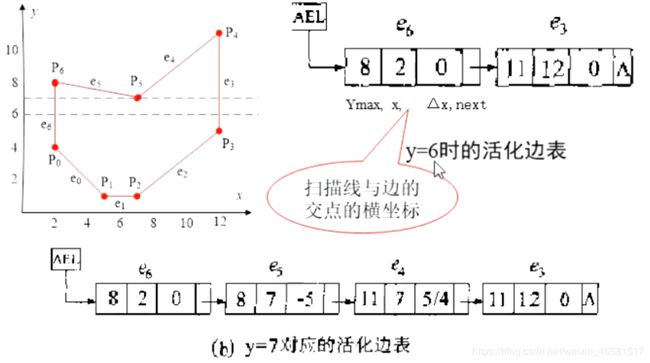
2.3.2.6 算法实现
- 建立边的分类表ET；
- 将扫描线纵坐标y的初值置为ET表中非空元素的最小序号；
- 置AEL为空；
- 执行下列步骤直至ET表和AEL表都为空；
2.3.2.7 算法特点
- 优点：利用边的 连贯性以加速交点的计算，利用ET以排除盲目求交，利用扫描线的连贯性以避免逐点判断，所以算法效率比逐点判断法高很多。
- 缺点：对各种表的维持和排序开销太大，适合软件实现而不适合硬件实现。
3. 区域填充
- 区域：已经表示成点阵形式的填充图形，它是像素的集合。
- 区域填充：将区域内的一点（常称【种子点】）赋予给定颜色，然后将这种颜色扩展到整个区域内的过程。
3.1 区域的表示方法
- 内点表示：
- 枚举出区域内部的所有像素；
- 内部的所有像素着同一个颜色；
- 边界像素着与内部像素不同的颜色；
- 边界表示：
- 枚举出边界上所有的像素；
- 边界上所有像素着同一颜色；
- 内部像素着与边界像素不同的颜色。
3.2 区域的类型
- 4连通
- 8连通
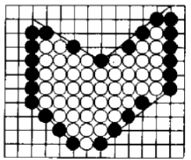
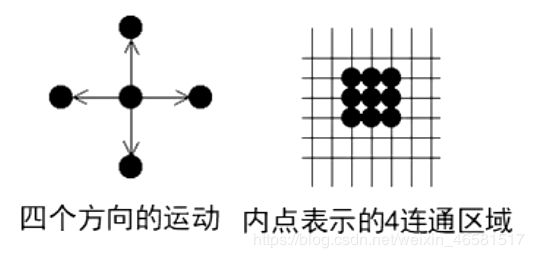
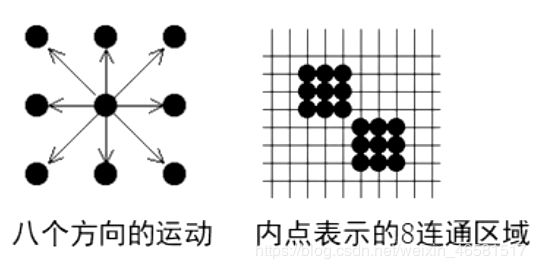
- 4连通区域的边界可以是8连通区域边界也可以是4连通区域边界。
- 8连通区域的边界必须是4连通区域边界。
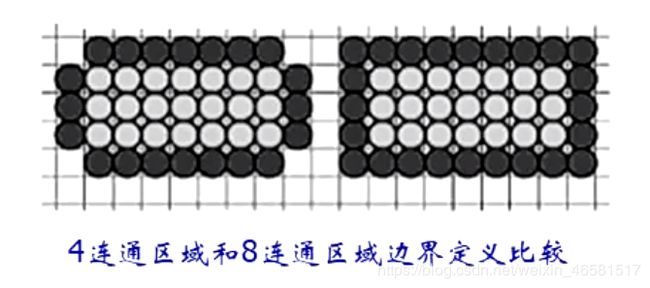
4连通区域边界填充算法的填充结果
8连通区域边界填充算法的填充结果
3.3 递归填充算法
3.3.1 内点表示4连通区域的递归填充算法
基本思想：从区域内部任一点（像素）出发，按照”右、上、左、下“的顺序判断相邻像素，若是区域内的像素，则对其填充，并重复上述过程，直至所有像素填充完毕。
void FloodFill4(int x, int y, int oldColor, int newColor) {
if(GetPixel(x,y) == oldColor) { // oldcolor表示区域的原色
Putpixel(x, y, newColor); // newColor表示区域的新颜色
FloodFill4(x+1, y, oldColor, newColor); // 右
FloodFill4(x, y+1, oldColor, newColor); // 上
FloodFill4(x-1, y, oldColor, newColor); // 左
FloodFill4(x, y-1, oldColor, newColor); // 下
}
} // end of FloodFill4
算法步骤：
种子像素入栈，当栈非空时，执行如下三步操作：
- 栈顶像素出栈；
- 将出栈像素置成多边形色；
- 按右、上、左、下的顺序检查与出栈像素相邻的四个像素，若其中某个像素不在边界上且未置成多边形色，则把该像素入栈。
- 特点：原理和程序简单，但效率不高，递归次数太多，费时费内存。
- 改进：减少递归次数，提高效率。可以采用扫描线填充算法。
3.3.2 扫描线填充算法
- 目标：减少递归层次；
- 范围：适用于内点表示的4连通区域；
- 算法思想：在任意不间断区域中只取一个种子像素（不间断区域指在一条扫描线上一组组相邻像素），填充当前扫描线上的该段区间；然后确定与这一区段相邻的上下两条扫描线上位于区域内的区段并依次把它们保存起来，反复进行这个过程，直到所所保存的各区段都填充完毕。
3.3.2.1 算法举例
- 初始化：种子像素入栈，当栈非空时，重复2-6的步骤；
- 栈顶像素出栈；
- 沿扫描线对种子像素的左右像素进行填充，直至边界，从而填满该区间；
- 区间内最左和最右像素分别记为 x L x_L xL和 x R x_R xR；
- 在区间 [ x L , x R ] [x_L, x_R] [xL,xR]中检查与当前扫描线相邻的上下两条扫描线是否全为边界或已经填充，若存在非边界、未填充的像素，将检查区间的最右像素作种子入栈；
- 当堆栈为空时，算法终止。
3.3.2.2 算法特点
- 该算法考虑了扫描线上像素的相关性，种子像素不再代表一个孤立的像素，而是代表一个尚未填充的区段。
- 进栈时，只将每个区段选一个像素进栈（每个区段最右边或最左边像素），这样解决了堆栈溢出的问题。
- 这样有机的组合：一边对尚未填充像素的等级（像素进栈），一边进行填充（像素出栈），既可以节省空间，又可以实施快速填充。
4. 多边形扫描转换与区域填充比较
-
联系：都是光栅图形面着色，用于真实感图形显示。可相互转换。
-
多边形扫描转换转化为区域填充问题：当给定多边形内一点为种子点，并用中点或DDA算法将多边形的边界表示成八连通区域后，则多边形的扫描转换转化为区域填充。
-
区域填充转化为多边形的扫描转换：若已知给定多边形的顶点，则区域填充转化为多边形的扫描转换。
-
不同点：
- 基本思想不同：前者是顶点表示转换成点阵表示，后者只改变区域内填充颜色，没有改变表示方法。
- 对边界的要求不同：前者只要求扫描线与多边形边界交点个数为偶数。后者区域封闭，防止递归填充跨界。
- 基本的条件不同：前者：从边界顶点信息出发（连贯性）。后者：区域内种子点（连通性）。