hdu5015——233 Matrix（矩阵快速幂）

Problem Description
In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 … in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333… (it means a0,1 = 233,a0,2 = 2333,a0,3 = 23333…) Besides, in 233 matrix, we got ai,j = ai-1,j +ai,j-1( i,j ≠ 0). Now you have known a1,0,a2,0,…,an,0, could you tell me an,m in the 233 matrix?

Input
There are multiple test cases. Please process till EOF.

For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 109). The second line contains n integers, a1,0,a2,0,…,an,0(0 ≤ ai,0 < 231).

Output
For each case, output an,m mod 10000007.

Sample Input
1 1
1
2 2
0 0
3 7
23 47 16

Sample Output
234
2799
72937

http://blog.csdn.net/u011721440/article/details/39401515

思路：

第一列元素为：
0
a1
a2
a3
a4
转化为：
23
a1
a2
a3
a4
3

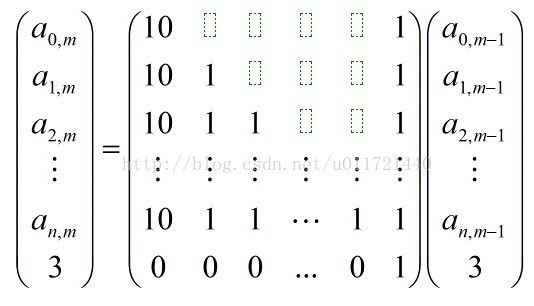
则第二列为：

23*10+3

23*10+3+a1
23*10+3+a1+a2
23*10+3+a1+a2+a3
23*10+3+a1+a2+a3+a4
3

根据前后两列的递推关系，有等式可得矩阵A的元素为：

照着上图构造矩阵就行了，真想不到这样也能找到递推式

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define INF 0x3f3f3f3f
#define MAXN 10000005
#define Mod 10000007
using namespace std;
const int N = 13;
long long m,n;
struct Matrix
{
    long long mat[N][N];
};
Matrix mul(Matrix a,Matrix b)
{
    Matrix res;
    for(int i=0; i<=n+1; ++i)
        for(int j=0; j<=n+1; ++j)
        {
            res.mat[i][j]=0;
            for(int k=0; k<=n+1; ++k)
            {
                res.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
                res.mat[i][j]%=Mod;
            }
        }
    return res;
}
Matrix pow_matrix(Matrix a,long long k)
{
    Matrix res;
    memset(res.mat,0,sizeof(res.mat));
    for(int i=0;i<=n+1;++i)
        res.mat[i][i]=1;
    while(k!=0)
    {
        if(k%2)
            res=mul(res,a);
        a=mul(a,a);
        k>>=1;
    }
    return res;
}
int main()
{
    Matrix tmp,arr;
    while(~scanf("%I64d%I64d",&n,&m))
    {
        memset(arr.mat,0,sizeof(arr.mat));
        memset(tmp.mat,0,sizeof(tmp.mat));
        arr.mat[0][0]=23;
        for(int i=1;i<=n;++i)
            scanf("%I64d",&arr.mat[i][0]);
        arr.mat[n+1][0]=3;
        for(int i=0;i<=n;++i)
        {
            tmp.mat[i][0]=10;
            tmp.mat[i][n+1]=1;
        }
        tmp.mat[n+1][n+1]=1;
        for(int i=1;i<=n;++i)
            for(int j=1;j<=i;++j)
                tmp.mat[i][j]=1;
        Matrix p=pow_matrix(tmp,m);
        p=mul(p,arr);
        long long ans=p.mat[n][0]%Mod;
        printf("%I64d\n",ans);
    }
    return 0;
}