《算法导论》学习之旅-第十章-基本数据结构

---

序言

在本章中，我们将会讨论如何使用指针的基本数据结构来构造动态集合，下面主要介绍：栈，队列，链表和有根树，此外还要介绍由数组构造对象和指针的方法。

栈和队列

栈和队列都是动态集合，对他们的删除操作都是设定好的。在栈中的删除操作采用的是先进后出策略；而在队列当中则是使用的是先进先出策略。下面将介绍如何使用简单的数组来实现这两种数据结构。

栈

栈的INSERT操作通常被称为压入(PUSH)，而删除操作则是成为弹出(POP)。这种数据结构就好比餐厅中的叠起来的盘中，我们每次都是上面放入，然后拿走的时候也是从最顶上的一个盘子拿走。

我们可以用一个数组来表示他，如，A[1…n]表示一个容纳最多有n个元素的栈，但有个栈顶属性A.top，它指向的是最新元素的位置，则栈包含的元素就是A[1…A.top]，其中A[1]表示栈底元素。

当A.top = 0的时候，这个栈就是空栈，通常我们会采用判空的函数进行判断（STACK-EMPTY），下面是判空，压入，和弹出操作的伪代码：

STACK-EMPTY(S)       //这是判空操作
if S.top == 0
	return TRUE
else return FALSE

PUSH(S, x)          //压入操作
S.top = S.top+1
S[S.top] = x

POP(S)				//弹出操作
if STACK-EMPTY(S)
	error "underflow"
else  S.top = S.top - 1
	return S.top[S.top+1]

上述的伪代码是比较简单的，如何压入操作的时候是没有考虑上溢出的情况。

队列

队列的INSERT操作称为入队，而DELITE则称之为出队操作。队列这种数据结构就像是食堂打饭时排队一样，遵循的是先排先出的原则。

利用Q[1…N]表示出最多可以容纳n-1个元素的队列.队列有一个属性：Q.tail 和 Q.head， Q.tail 指向下一个新元素要插入的位置，Q.head 指向队头元素。当Q.head = Q.tail时队列为空，当Q.head = Q.tail+1表示队满。

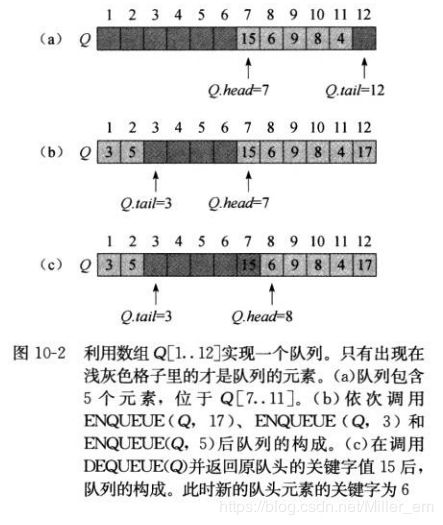
下面的入队和出队操作的伪代码(省略了对上溢和下溢的检测)：

ENQUEUE(Q, x)				//入队操作
Q[Q.tail] = x
if Q.tail == Q.length
	Q.tail = 1
else Q.tail = Q.tail + 1

DEQUEUE(Q)					//出队操作
x = Q.head
if Q.head = Q.length
	Q.head = 1
else Q.head = Q.head+1
return 1

这两种操作的时间都是O(1)

链表

链表(linked list)是一种这样的数据结构，其中的各对象按线性顺序排列。数组的线性顺序是由数组下标决定的，然而与数组不同的是，链表的顺序是由各个对象里的指针决定的。链表为动态集合提供了一种简单而灵活的表示方法。

链表有单链表和双链表及循环链表。书中着重介绍了双链表的概念及操作，双链表L的每一个元素是一个对象，每个对象包含一个关键字:key和两个指针：next和prev。链表的操作包括插入一个节点(insert)、删除一个节点(delete)和查找一个节点(search)，如果双链表的对象L.prev = NIL 则表示链表的头，L.next = NIL 则表示链表的尾。下面是双链表的示意图：

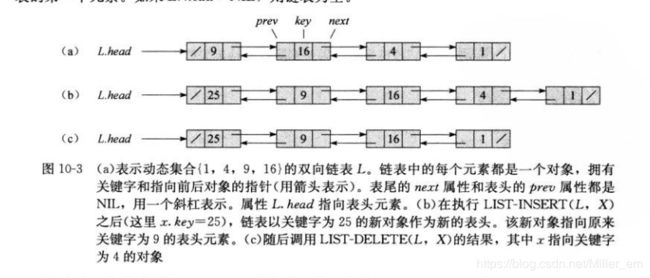
而单链表时省略掉了L.prev指针。循环链表的表头指针L.prev指向的是表尾元素的位置，我们可以将一个循环链表看成是一个圆环。

下面介绍几种链表的操作：

链表的搜索

链表的搜索操作是采用的简单线性搜索方法，主要用于查找链表L中的第一个关键字K的元素，如果链表中没有该对象，则返回NIL。搜索操作的伪代码为：

LIST_SEARCH(L, k)
x = L.head
while x != NIL and x.key != k:
	x = x.next
return x

要搜索一个有n个对象的链表时，最坏情况的运行时间为O(n)

链表的插入

插入操作是将要插入的x结点连接在链表的前端，如伪代码所示：

LIST-INSERT(L, x)
x.next = L.head
if L.head != NIL 
	L.head.prev = x
L.head = x
x.prev = NIL

一个含有n个元素的链表执行的运行时间是O(1)

链表的删除

删除过程就是将一个元素x从链表L中移除，如：

LIST-DELETE(L, x)
if x.prev != NIL
	x.prev.next = x.next
else L.head = x.next
if x.next != NIL
	x.next.prev = x.prev

删除操作的时间，分为两种情况：1.删除一个元素，则他的时间是O(1)
2. 如何是删除某一个关键字为k的元素，则最坏的情况下可能用到的时间为O(n)

指针和对象的实现

有些语言不支持指针和对象数据类型时，我们需要实现链式数据结构的两种方法，下面我们将介绍数组和数组下标来构造对象和指针。

对象的多数组表示

对每个属性都用一个数组表示。如下图所示：

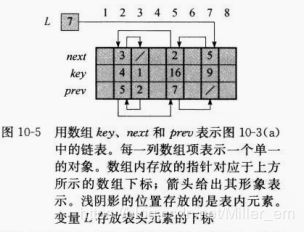
prev和next数组中存放的数字就是他们所指向节点的位置，此外变量L存放的是表头元素的下标

对象的单数组表示

计算机中的内存往往是从整数0到M-1进行编址。用一个数组来表示一个链表，对于双链表就是连续的三个单元表示一个结点。如下图所示：

有根树的表示

这一小节将讨论用链式储存结构表示有根树的问题，首先我们先讨论二叉树，然后给出针对节点的孩子数任意的有根树的表示方法。

二叉树

下面是二叉树的示意图：

二叉树的每一个节点都含有父节点p，左孩子left，右孩子right的指针。如果x.p = NIL,则x为根节点。如果x.left和x.right都是NIL，则则表示x为叶结点。属性T.root指向整棵树T的根结点，如果T.root = NIL， 则树为空。

分支无限制的有根树

二叉树的表示方法可以推广到每个结点的孩子数都至多为常数k的任意类型的树：只需要将left和right属性用child₁ ， child₂ ，…，child_k来表示。但是由于孩子数的不定性，我们就不知道改为其分配多少个数组。此外，及时孩子数k限制在一个大的常数以内，若多数的节点都只有少量的孩子，则会浪费大量的空间。

下面就有一种叫做左孩子右兄弟表示法可以解决该类问题。这种方法和前面的类似，每个结点都包含一个父节点指针p，且T.root指向树T的根结点
。然而每个结点就只包含两个指针：

1. x.left-child指向的结点x最左边的孩子结点
2. x.right-sibling指向的是x右侧相邻的兄弟结点

如果结点x没有孩子结点， 则x.left-child = NIL；如果结点x是其父节点的最右孩子，则x.right-sibling = NIL。