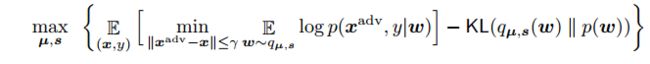[论文笔记]集成方法提高神经网络的对抗鲁棒性

一、多个弱防御的集成不能形成强防御

参考文献：Adversarial Example Defenses: Ensembles of Weak Defenses are not Strong.2017.

1.攻击者

假设攻击者知道模型的各种信息，包括模型架构、参数、以及模型的防御策略（白盒攻击）。
考虑两种白盒攻击者：
（1）静态
不知道模型的防御策略，因此静态攻击者可以利用现有的方法生成对抗样本，但不针对特定的防御策略。
（2）动态
知道模型的防御策略，可以自适应地制定攻击方法，比静态攻击者更强大。

2.防御策略

（1）feature squeezing
包括两个检测组件：reducing the color depth to fewer bits 和spatially smoothing the pixels with a median filter
（2）specialist-1 ensemble method
根据对抗混淆矩阵将数据集分成K+1个子集，形成由K+1个分类器组成的一个集成分类器
（3）多个检测器集成
包括Gong、Metzen、Feinman三个人提出的对抗样本检测器；

其中（1）和（2）都是前人特意构造的由多个组件构成的防御策略，并且对于静态攻击的产生的低干扰对抗样本的防御效果很好。（3）是本文作者将现有的多个检测器集成起来的防御策略。

3.对抗样本生成方法

利用优化方法生成对抗样本，最小化如下损失函数：
$$loss(x^{\prime })=||x^{\prime }-x|{|}_2^2+cJ(F_{\theta }(x^{\prime }),y)$$
其中c为超参数，该方法也称为CW攻击方法。

4.干扰大小的度量

用下式度量对抗样本与干净样本之间差异：
$$d(x^{\ast },x)=\sqrt{\sum _i(x^{\ast }-x{)}^2}$$
其中样本点都被归一化[0,1]之间。

5.实验

5.1 攻击 feature squeezing
结论：feature squeezing 不是一种有效的防御方法。首先单独用某种squeeze方法都仍然可以生成对抗样本对模型产生攻击，其次多种squeeze结合也会收到对抗样本的攻击。

5.2 攻击 ensemble of specialists
ensemble of specialists-1也不能保证对抗样本具有很低的分类置信度。

5.3 攻击多个检测器集成
在一定程度上会提高对抗样本与干净样本的距离，但是不是很显著。

6.结论

自适应的攻击方法可以设计出具有很小扰动的对抗样本来攻击这三种防御方法和其组件，因此对抗样本在各个防御组件之间具有迁移性。
在评价模型的防御效果时，应该考虑两方面：
（1）使用更强的攻击方法，如FSGM不如迭代优化的攻击方法强；
（2）使用自适应的攻击方法（动态），使得模型能够对于那些知道模型防御机制的攻击者同样具有抵抗性。

二、简单集成神经网络

参考文献:Ensemble Methods as a Defense to Adversarial Perturbations Against Deep Neural Networks 2017.

1.攻击方法

（1）Fast Gradient Sign Method
（2）Basic Iterative Method

2.集成模型

（1）多个分类器具有相同的网络结构，但是具有不同的初始化权重；
（2）多个分类器具有相似的网络结构；
（3）bagging，即对训练数据集采样产生多个训练子集，分别在各个子集上训练分类器；
（4）对训练数据集添加高斯噪声。

3.计算梯度

（1）使用第i个分类器的梯度
（2）使用所有分类器梯度的平均（实验结果显示该方法更好）

4.实验

所有实验都是10个分类器的集成。

5.结论

集成神经网络不仅能够提高测试精度，而且能够提高分类器对对抗样本的鲁棒性。

三、 ensemble of specialists

参考文献：ROBUSTNESS TO ADVERSARIAL EXAMPLES THROUGH AN ENSEMBLE OF SPECIALISTS.2017.

1.利用FGSM方法得到模型的混淆矩阵：

根据混淆矩阵将数据分为2K+1个子集，在每个子集上训练分类器。

2.伪代码如下：

3.实验考虑三种模型

单个CNN，简单集成CNN，specialists +1，其中每个卷积网都是（32+32+64+全连接+softmax。

4.实验结果

specialists +1方法能够很好地区分对抗样本和干净样本，拒绝可疑的样本，从而提高对各种对抗样本的稳定性。

四、随机自集成

参考文献：Towards Robust Neural Networks via Random Self-ensemble.2018.

1.思想

RSE是通过给神经网络中加入噪声层来使得神经网络对对抗干扰更加稳定。该算法等价集成无穷个噪声模型，并且不会增加内存消耗。噪声随机梯度下降可以保证集成模型有很好的预测能力。

2.taget攻击与untarget攻击

对于攻击者：target攻击比untarget攻击更难；对于防御者，untarget攻击比target攻击更难。

3.网络设计

在每个卷积层前都加入噪声层：

4.伪代码如下：

5.理论分析

RSE可以达到原来网络预测精度的原因是：在训练过程中相当于最小化测试误差的上界。
RSE等价于Lipschitz正则。

6.结论

RSE可以提高神经网络的鲁棒性，对于十分强大的白盒攻击十分鲁棒。方法简单，可以嵌入到任何神经网络。

五、集成对抗训练

参考文献：ENSEMBLE ADVERSARIAL TRAINING:ATTACKS AND DEFENSES.2018.

1.前言

利用快速一步生成对抗样本来进行对抗训练仍然受到黑盒攻击的威胁，原因是这种形式的对抗训练会收敛到退化全局最小值，数据点附近的小曲率模糊了损失函数的线性近似。论文提出了一种集成对抗训练的方法，它是利用其它模型产生的干扰来生成对抗样本。在ImageNet上，集成对抗训练产生的模型对黑盒攻击表现出了强大的鲁棒性。

2.对抗训练

Mardry(2017)提出，对抗训练可以解释为一个给定的攻击在数据集上的最大化问题和最小化问题：
$$h^{\ast }=\underset{h\in H}{\mathrm{argmin}}\underset{(x,y_{true})\in D}{E}[\underset{||x^{adv}-x|{|}_{\infty }\le ϵ}{\max }L(h(x^{adv}),y_{true})]$$
但是在本文实验中，采用Szegedy(2013)和GoodFellow(2014)提出的同时用干净样本和对抗样本来训练。

3.集成对抗训练

本文提出了一种简单的方法来解耦对抗样本的生成和模型的训练，同时可以明确地将黑盒攻击的鲁棒性联系起来。该方法称为“集成对抗训练”。用其它模型产生的对抗样本来训练。由于对抗样本具有迁移性，因此其它模型产生的对抗干扰近似上述目标函数中的最大化问题。最小化训练误差意味着增加模型对黑盒攻击的鲁棒性。

六、对抗训练贝叶斯神经网络(adv-BNN)

参考文献：ADV-BNN: IMPROVED ADVERSARIAL DEFENSE THROUGH ROBUST BAYESIAN NEURALNETWORK.2018.

1.前言

首先，尽管最近的研究表明引入随机性可以提高神经网络的稳定性，但是我们发现盲目地给各个层添加噪声不是引入随机性的最优方法。我们可通过贝叶斯神经网络来学习模型的后验分布。第二，我们建立的BNN中的最小最大问题来学习对抗攻击下的最优的模型分布，称为“对抗训练贝叶斯神经网络”。

2.PGD攻击

CW和PGD是公认的两种表现不俗的攻击方法。PGD攻击比CW攻击好的一点在于：PGD攻击可以通过改变$\gamma$来直接控制干扰量，而CW攻击需要调整损失函数中的超参数c，这显然没有PGD更为直接。

PGD攻击的目标函数为：
$$\underset{||\delta |{|}_{\infty }\le \gamma }{\max }l(f(x_0+\delta ;w),y_0)$$
PGD攻击可以利用投影梯度下降来迭代更新对抗样本：
$$x^{t+1}={\Pi }_{\gamma }\{x^{t+1}+\alpha sign({\nabla }_{x}l(f(x_0+\delta ;w),y_0))\}$$
其中${\Pi }_{\gamma }$为集合$\{x|||x-x_0|{|}_{\infty }\le \gamma \}$.

对于随机神经网络，攻击者试图寻找寻找一个通用的干扰来欺骗大多数随机权重。该通用干扰可最大化损失函数的期望来获得：
$$\delta =\underset{||\delta |{|}_{\infty }\le \gamma }{\mathrm{argmax}}\underset{w}{E}[l(f(x_0+\delta ;w),y_0)]$$
该优化问题与PGD和CW的求解方法类似，唯一的区别是我们需要在每次迭代时对$w$进行采样。

3.BNN

对于观测随机变量$（x,y）$,我们的目标是估计隐变量$w$的分布。给定先验分布$p(w)$，后验分布为：
$$p(w|x,y)=\frac{p(x,y|w)p(w)}{p(x,y)}$$

后验分布的分母是一个无穷积分，因此该后验分布很难计算。通常有两种处理方式：
（1）SGLD：在不知道闭式解的情况下采样$w\sim p(w|x,y)$
该方法的本质是带高斯噪声的随机梯度下降，很容易实现。但是每次minbatch迭代只能得到一个样本，对快速推断不是很有效。并且随着SGLD中步长${ϵ}_t$减小，样本之间的相关性增大，因此需要生成更多的样本来保证具有一定的方差。

（2）利用某一参数分布$q_{\theta }(w)$来近似 $p(w|x,y)$，其中$\theta$的确定可通过最小化 $KL(q_{\theta }(w)||p(w|x,y))$
该变分推断是生成样本的有效方法，因为我们通过最小化KL散度后知道近似后验分布$q_{\theta }(w)$。为了简单起见，我们可以假设近似后验分布是全分解高斯分布：
$$q_{\theta }(w)={\Pi }_{i=1}^d{q}_{{\theta }_i}(w_i)and{q}_{{\theta }_i}(w_i)=N(w_i;{\mu }_i,{\sigma }_i^2)$$
当变量之间相关性比较大时，该简单形式会导致$q_{\theta }(w)$与$p(w|x,y)$存在很大偏差。

4.adv-BNN

我们将对抗训练（Mardry 2017）与BNN结合起来。

假设联合分布$q_{\mu ,s}(w)$是全分解的，每一部分$q_{{\mu }_i,s_i}(w_i)$服从均值为${\mu }_i$,标准差为$exp(s_i)$的正态分布。先验分布为等距高斯分布$N(0_d,s_0^2{I}_{d\times d})$.

对于任意两个高斯分布$s$和$t$,其KL-divergence为：

变分推断：
方法一：

法二：

则adv-BNN的变分推断证据下界为：