数值优化（Numerical Optimization）学习系列-信赖域方法

信赖域方法和线搜索类似都是迭代方法，与其不同的是，每次迭代时，在一个选定的可信赖区域内，选择当前迭代点的近似模型 mk ，然后计算最优步长；如果步长不合适，可以对区域进行缩放。该小结主要介绍：

1. 信赖域方法的基本形式
2. 求解信赖域的基础方法
3. 信赖域方法的收敛性和收敛速度
4. 信赖域方法的扩展

信赖域方法的基本形式

在信赖域方法中，可信赖的区域（Region）的选择很重要，一般都会根据上一步结果进行动态变化；如果上一步太大则缩小，否则进行扩大。
在模型最优化问题中，选择TR方法比LS方法能够较快的收敛，例如
在该例子中，在非凸函数F中，当前步骤TR方法要优于LS。
信赖域方法有几个参数需要选择：
1. 近似模型 mk
2. 可信赖区域 Δk
3. 求解参数 pk

基本形式

在本节中模型选择为二次近似模型，采用函数二阶泰勒展开，即

f(xk+p)=fk+gTkp+12pT∇2fkp

一般情况下会用 Bk 去近似Hessian矩阵，即

mk=fk+gTk+12pTBkp

其中 Bk 为对称矩阵。

信赖域的基本形式为：

min mk(p)=fk+gTk+12pTBkps.t ||p||≤Δk

该问题为关于p的带约束的最优化问题，参数p被限制在一个球形区域内。如果 Bk 选择为Hessian，则为TR的牛顿方法。
如果 ||B−1kgk||≤Δk 则 pk=−B−1kgk 为 完全步(Full Step)，即球形约束没有作用。

Δk 的选择

参数 Δk 的选择一般会根据上一步的结果进行调整，定义

ρk=fk−f(xk+pk)mk(0)−mk(pk)

其中分子表示函数实际减小的值；分母表示近似模型减少的值。分析 ρk :
1. 如果 ρk 小于0，一般情况下分母不可能小于0，因为目标函数求解的是最小值；此时说明分子小于0，即下一个目标点比上一步大，此时需要舍弃。
2. 如果 ρk 大于0并且接近1，说明模型和实际的预期比较相符合，此时可以考虑扩大 Δk
3. 如果 ρk 大于0但是明显小于1，此时可以不用调整
4. 如果 ρk 大于0，但是接近0，说明模型变化范围比较大，但是实际改变比较小，此时应该收缩或者减少 Δk
具体算法如下：

子问题的最优解

为简化形式，将信赖域问题的子问题表示为：

min m(p)=f+gTp+12pTBps.t ||p||≤Δ

该问题为标准的带不等式约束的二次优化问题，可以根据KKT条件（后面会深入介绍）得到该问题的最优解
定理
如果向量 p∗ 为子问题的最优解，当且仅当满足 p∗ 为可行解，并且存在标量 λ 满足

(B+λI)=−g(a)λ(Δ−||p∗||)=0(b)(B+λI)正定(c)

其中条件（b）为补充条件，即要么 λ为0要么Δ=||p∗|| 。
从下图中可以看出最优解和参数 λ 的关系

当参数 Δ=Δ1 时，最优解为 p3 此时相当于没有约束，此时 λ=0
当参数 Δ=Δ1或者Δ2 时，最优解被球形约束限制，此时满足 Δ=||p∗|| ，根据上面条件（a）有

λp∗=−Bp∗−g

如果能够找到这样的p满足这些条件就能找到最优解。

基于柯西点（Cauchy-Point）的算法

在实际求解过程中不一定找到最优解，而是找到一个充分下降的点满足全局收敛即可。柯西点就是满足该条件的点（ pck ）

柯西点（Caychy-Point）算法

求解步骤如下
1. 计算原子问题的线性蜕化问题，寻找向量 psk 满足

psk=arg min fk+gTkps.t. ||p||≤Δk

2. 寻找标量 τk>0 满足 min mk(τpsk) 同时满足信赖域的约束，即

τk=arg min mk(τpsk)s.t. ||τpsk||≤Δk

3. pck=τkpsk

分别解释如下：
1. 计算 psk 从上述步骤1中可以看出求解步骤1有必使解， psk=−Δk||gk||gk 。两种思路，一是退化后的函数为线性函数，而且是递减的，只要取下界即可。二是利用KKT条件也可以推出。
2. 将求解得到的 psk 代入子问题可以得到，

min m(p)=f+gTp+12pTBps.t ||p||≤Δmin m(τpsk)=f−gTτΔk||gk||gk+12τ2Δk||gk||gTkBkΔk||gk||gks.t. ||τpsk||≤Δk

是一个关于 τ 的二次函数，如果
1） gTkBkgk≤0 ，是一个关于 τ 的递减函数，直接得到 τ=1
2)如果 gTkBkgk>0 求导可以得到 τk=||gk||3ΔkgTkBkgk,同时τ需要满足τ\e1

柯西点很容易计算，但是如果只利用柯西点，相当于只利用了梯度方向，相当于线搜索的扩展而已，即收敛速度为线性收敛。

Dogleg算法

该方法适用于当 Bk正定时 ，寻找半径 Δ 和最优解 p∗(Δ) 之间的关系。
在之前定义了完全步(Full Step)，即 ||B−1kgk||≤Δk 则 pBk=−B−1kgk
该算法的思路为， p∗(Δ) 表示不同 Δ 条件下的最优解，
1） p∗(Δ)=pB||pB||≤Δ ，否则
2）

p(τ)=⎧⎩⎨τpu,pu+(τ−1)(pB−pu),0<τ<11<τ<2

其中 pu 定义为

pu=−gTggTBgg

，沿着梯度方向的最优解。
此为Dogleg方法，即寻找一个折线即两个线段的交点，即一条线段是沿着负梯度方向的最优值；二是沿着 pU到pB 方向。在此折线上寻找最优解。
由定理可以证明 ||p(τ)||是一个关于τ的递增函数，而m(p(τ))是一个关于τ的递减函数 ，又是一个线性函数，因此只要计算 p(τ)和||p||=Δ 的交点即可。从下图可以清晰看到

二维子空间最优化

在DogLeg算法中，可以理解为最优解 p∗ 可以表示为 pU和pB的扩展子空间，即p∗=λ1g+λ2B−1g ，则原子问题可以表示为：

min m(p)=f+gTp+12pTBps.t ||p||≤Δp∈span[g,−B−1g]

迭代算法

根据子问题的最优解形式可以得到
1）当 λ=0时 需要满足

Bp∗=−gB正定||p∗||≠Δ

2) 当 λ≠0时 需要满足

(B+λI)p∗=−gB+λI正定||p∗||=Δ

即

||p∗||=||−(B+λI)−1g||=Δ

通过定义 p(λ)=−(B+λI)−1g ，寻找特定的 λ使得||p(λ)||=Δ

相关定义

由于B正定因此可以进行正交分解, B=QΛQT； Λ=diag(λ1,λ2,...,λn)并且λ1≤λ2≤...≤λn

B+λI=Q(Λ+λI)QTp(λ)=Q(Λ+λI)−1QTgp(λ)2=−∑1n(qTjg)2(λj+λ)2

由于是正交分解因此 qiqj=1

迭代算法

1）由上述定义

p(λ)2=−∑1n(qTjg)2(λj+λ)2

可以看出
2） 当 λ>−λ1时 函数值是一个单调递减函数，特别当 limλ→∞(p(λ)2)→0
3)因此我们需要寻找 λ∈(−∞,λ1)使得||p||=Δ

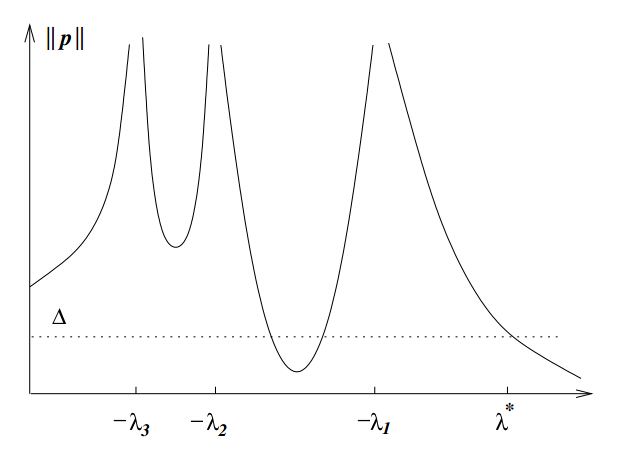
λ 求解

在 qTig≠0
1）通过牛顿迭代法求解

ϕ(λ)=||p(λ)||−Δ=0

2）近似算法求解

ϕ1(λ)=C1λ+λ1+C2phi1(λ)=1Δ−λ+λ3C3

当 qTig=0 是一个Hard Case，此时可以添加一个误差因子进行近似

p(λ)=Q(Λ+λI)−1QTg+τE

信赖域的其他扩展

1. poor scaling问题，可以扩展为球形或者椭圆形
2. 可以构造Scaled的算法
   min m(p)=f+gTp+12pTBps.t ||Dp||≤Δ
3. 矩阵D的构造和 ∂2f/∂xi 相关
4. 可以构造通用的柯西点废
5. 其他Norm方法，例如
   ||p||1≤Δ||p||∞≤Δ

总结

通过该节需要了解
1. 信赖域方法和线搜索方法的不同
2. 信赖域方法的基本形式
3. 信赖域方法的柯西点算法、DogLeg算法和最优解迭代算法
4. 信赖域方法收敛