ACM_状压DP
引言
状压DP: 状态压缩DP的缩写, 用数字的进制(二进制居多)来表示问题的状态, 用动态规划的思想不断后推, 得到最后得到问题的解的一种解题技巧. 本文将以:
1. 常用的关于状态的操作(放在前面方便以后查询)
2. 状态的解释
3. 与动态规划结合得到答案
4. 例题
的方式介绍状压DP
常用操作:
意思 表示方法 空集 0 只含有第i个元素 1 < < i 含有所有元素 (1 < < n )-1 判断第i个元素在不在集合内 if(s > > i & 1) 加入第i个元素 s \ 1 < < i 删除第i个元素 s & ~(1 < < i) S 和 T 的并 S \ T S 和 T 的交 S & T 枚举所有集合 for(int s = 0; s < 1 < < n; ++s) 2.高级操作:
枚举某个集合(sup)的子集:``` int sub = sup;//sub代表子集 do { //对子集的操作 sub = (sub - 1) & sup; } while(sub != sup); //这种操作是: //每次找到最后1个1的位置 假如是p //sub的p位置的1变成0 //sub的p后面的位置变成 和sup一样 //比如对于sup = 101101 那么就应该是 101100 101001 101000 100101 // 100100 100001 100000 001101 001100 001001 001000 000101 //000100 000001 000000枚举有k个元素的子集 :
int comb = (1 < < k) - 1;//comb代表所求集合 while(comb < 1 < < n) { //对集合的操作 int x = comb & -comb, y = comb + x; comb = ((comb & ~y) / x > > 1) | y; } //这个我没懂, 不过拿来用没错PS: 来自《挑战程序竞赛》P156
状态
PS: xxx(y) 代表的意思是一个数是xxx它是在y进制下
一般用数字的进制表示物体的状态, 最常见的是二进制, 0 表示没有这个东西, 1 表示有这个东西, 比如有A B C三个物体, 每个物体可有可无, 如何得到所有可能的集合呢? 我们用数字二进制下的第一位代表A, 第二位代表B, 第三位代表C 那么 100(2) 代表的就是有C, 无A, 无B 101(2)代表的意思如下图
如何表示所有的集合呢? 只需要for(int i = 0; i < 1 << 3; ++i) 就可以了
for(int s = 0; s < 1<<3; ++s) {
对集合的操作;
}表面上的数字是十进制 但是实际上对集合的操作是基于二进制下的有时候也需要三进制, 比如表示一个物品没有出现, 出现了一次, 出现了两次, 一共三种状态, 就需要三进制了, 但是计算机里面没有现成的三进制的运算, 这时候我们可以打表
比如
f[0] = 1;//f[i] 表示的是3的i次方, 也就是第1 << i 的值(三进制下)
for(int i = 1; i < N; ++i) f[i] = f[i-1] * 3;
//vis数组就是需要得到的查询对应位置是多少的表
for(int s = 0; s < 1<//N是物品的最大个数
int tmp = s;
for(int j = 0; j < N; ++j) {
vis[s][j] = tmp % 3;//vis表示的就是s状态的第j个数是多少
tmp /= 3;
}
}
//打表的效率明显可以看出来是O((1< 对于增加删除元素用加减就行了 比如第i位加1
if(vis[s][i] != 2) s += f[i]同理更高进制也可以类似的表示
3. 结合动态规划, 一般设置的状态都会和集合有关dp[s] (可能不止一维) 比如从s中的i地方到j地方 dp[s | (1 < < j)] = dp[s] + g[i][j] 或许用下面的例题解释更好
4. 例题
例题1:
题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=1074
;
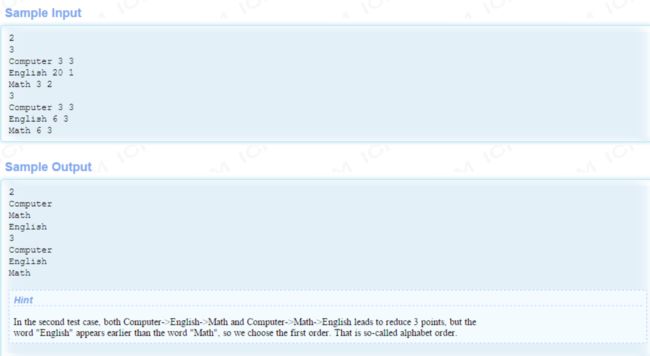
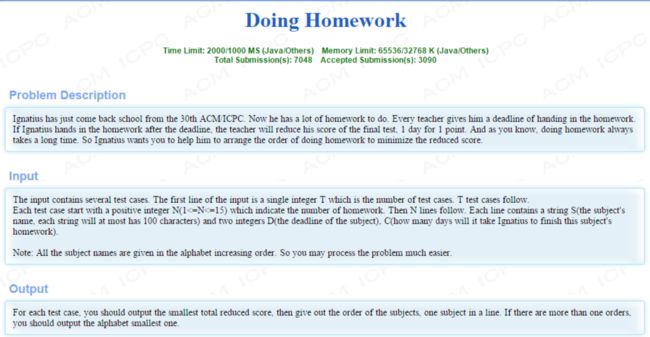
题目大意: 小明做作业, 每项作业有个截止日期d[i], 有个完成作业需要的时间c[i], 如果作业晚交一天, 那么久要扣1分, 问怎么作业扣的分最少
1 <= n <= 15
做题思路:
首先看到n的范围就有很强的状压dp的感觉 n <= 15
然后做作业无非就是有个顺序, 比如这里s = 10010表示已经做完了第1和第4个作业 现在转移状态到11010 或者 10110 或者 10011我们当然把所有的都算出来 然后取最小就可以了 直到转移到11111的状态 关于先做哪个用个pre数组就可以轻松解决了 输出即可
code :
#include 1<1<int n, c[N], d[N], ans[N];
string subj[N];
int main() {
int T; scanf("%d", &T);
while(T--) {
memset(dp, 0x3f, sizeof dp);
scanf("%d", &n);
for(int i = 0; i < n; ++i) {
cin >> subj[i] >> d[i] >> c[i];
}
for(int i = 0; i < 1 << n; ++i) {
int tmp = 0;
for(int j = 0; j < n; ++j)
if(i & (1<0] = 0;
for(int i = 0; i < 1 << n; ++i) {
for(int j = 0; j < n; ++j) {
if((i & (1<0) {
int other = t[i|(1<0);
if(dp[i] + other < dp[i|(1<1<1<int tmp = (1<1;
int k = 0;
while(tmp) {
ans[k++] = pre[tmp];
tmp = tmp & (~(1<cout << dp[(1<1] << endl;
for(int i = n-1; ~i; --i) cout << subj[ans[i]] << endl;
}
} 解释一下
t[s] s代表的是状态, t[s]代表的是到达这个状态需要的时间那么假如最后完成的是第i个作业, dp[ s | (1< < i ) ] 就等于 min(dp[ s | ( 1 < < i], dp[s] + t[s | ( 1 < < i)] - d[i])表示的意思就是 对于每个dp[s]可以推出它的所有下一个状态, 并且是需要扣得分数是 此状态所扣得分数 + (到达这个状态的时间 - 截止时间) 当然下个状态要取最小值.
对于为什么状态要for(int s = 0; s < 1 < < n; ++s) 即从小到大 因为每个状态s都是由比它小的状态更新而来(比如1001 由0001 和 1000 而来, 两个数都比它小) 所以从小到大就可以保证每次到达的s已经被全部更新了)
例题2:(结合flord算法的状压DP)
题目链接 http://acm.hdu.edu.cn/showproblem.php?pid=4856
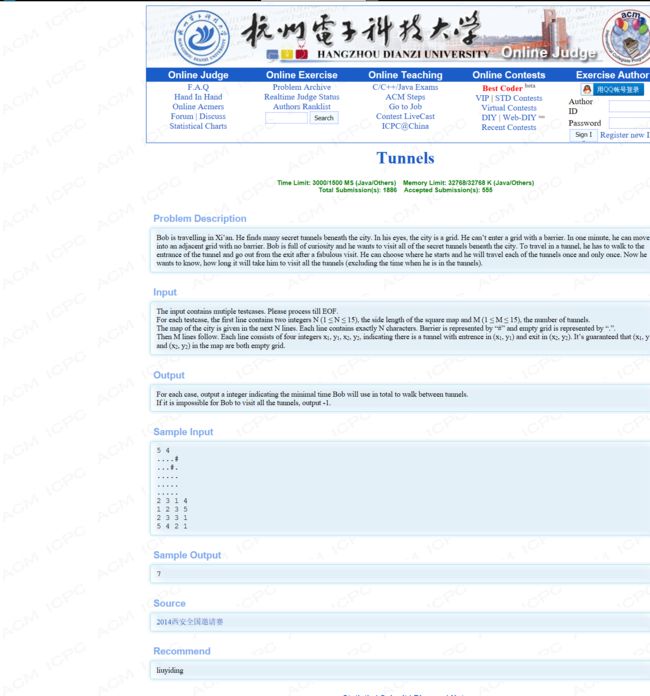
题目大意: 小明去西安, 他在一个长为n宽为m的网格中, 这个网格有很多隧道, 每个隧道有个入口有个出口, 从入口进去可以从出口出来, 小明在一个地方可以选择向上下左右4个方向走, 花费一个单位时间, 如果这里有隧道, 也可以选择走隧道入口进去, 出口出来, 这里不花时间, 小明可以从任意位置出发, 问小明想拜访完所有的隧道, 所需要的最少时间是多少?
1 <= n <= 15
做法:
又是n <= 15 所以很可能是状压DP(废话, 这里讲的就是这个)
最开始想状态可能想到dp[s][x][y] s 表示走了的隧道情况, x y 代表现在的坐标; 但是状态转移会麻烦一点, 后来想到因为时间要最少, 所以最后得到的解得时候小明一定在某个出口位置, 所以不需要x, y, 可以先把入口和出口的所有点都表示出来, 设置状态dp[s][i] s代表走了的隧道情况, i代表现在在哪个出口点, 最开始小明一定会从某个入口进入, 到达这个隧道的出口, 所以初始化for(int i = 0; i < in_n; ++i) dp[1< < i][i] = 0; in_n代表入口的个数, 状态转移, 因为小明每次出来的时候必定会向下一个入口进发, 所以用flord求出任意两点的最短距离, 就可以实现从这个点到下一个点, 直到更新完所有的点, 答案就出来了
code
#include struct P {
int x, y;
P (int x = 0, int y = 0) : x(x), y(y) {}
};
P in[N], out[N];
string sto[N];
int dx[] = {0, 1, 0, -1}, dy[] = {-1, 0, 1, 0};
int main() {
while(cin >> n >> m) {
for(int i = 0; i < n; ++i) cin >> sto[i];
memset(g, 0x3f, sizeof g);
for(int y = 0; y < n; ++y) {
for(int x = 0; x < n; ++x) {
g[y][x][y][x] = 0;
for(int i = 0; i < 4; ++i) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if(sto[y][x] == '.' && sto[ny][nx] == '.') g[y][x][ny][nx] = 1;
}
}
}
for(int ky = 0; ky < n; ++ky) for(int kx = 0; kx < n; ++kx) {
for(int iy = 0; iy < n; ++iy) for(int ix = 0; ix < n; ++ix) {
for(int jy = 0; jy < n; ++jy) for(int jx = 0; jx < n; ++jx) {
g[iy][ix][jy][jx] = min(g[iy][ix][jy][jx], g[iy][ix][ky][kx] + g[ky][kx][jy][jx]);
}
}
}
for(int i = 0; i < m; ++i) {
cin >> x >> y >> u >> v;
--x, --y, --u, --v;
in[i] = P(x, y);
out[i] = P(u, v);
}
memset(dp, 0x3f, sizeof dp);
for(int i = 0; i < m; ++i) dp[1<0;
for(int i = 0; i < 1 << m; ++i) {
for(int j = 0; j < m; ++j) {
if(i & (1<for(int k = 0; k < n; ++k) {
if((i & (1<0) {
dp[i|(1<1<// printf("i = %d j = %d k = %d dp[%2d][%2d] = %10d dp[%2d][%2d] = %10d\n",i, j, k, i|(1<
}
}
}
}
}
int ans = INF;
for(int i = 0; i < m; ++i) ans = min(ans, dp[(1<1][i]);
if(ans == INF) ans = -1;
cout << ans << endl;
}
} 这个题需要用到状压DP和Flord 感觉这两个东西结合起来的题还是很多….
