连通分量

图论 连通分量

0.1 概述

图论中，或者説OI中研究的连通分量主要有三种：强连通分量、点双连通分量、边双连通分量。本文并不打算着重讲述\(tarjan\)算法的具体实现，默认读者已掌据此前置知识。

1.1 强连通分量

强连通分量是指：在有向图中，强连通分量中的任意两点(\(u\),\(v\))，存在\(u\rightarrow v\)和\(v\rightarrow u\)的两条不同路径。

极大强连通分量：无法继续扩张的强连通分量。在通常语境下，一般默认“强连通分量”指的就是"极大强连通分量"

算法实现：\(tarjan\)算法可以做到\(O(n)\)效率地求解。

1.2 例题：[USACO15JAN]草鉴定Grass Cownoisseur

洛谷传送门

可以发现，将图缩点染色后，一个分量内的点之间可以任意到达。即：答案的最小值等于1号草场所处分量的大小。

在已经缩点后的图上计算由1号草场所在分量向其余分量求最长路\(dis1\)，再求由其余分量向1号草场所在分量的最长路\(dis2\)（建反边）

对于原图上存在的一条边\(u\rightarrow v\)，如果这两个点同处一个连通分量上，在这条边上逆行一次是没有任何意义的；但是如果这两个点并不在一个连能分量上，那么可以：先走到\(v\)所在的分量dis1[v分量],再逆行回到u分量，然后回到1号草场分量dis2[u分量]，最后逛完1号分量siz[1号分量]。因此:

ans=max(ans,dis1[v]+dis2[u]+size[1分量]

2.1 点双连通分量

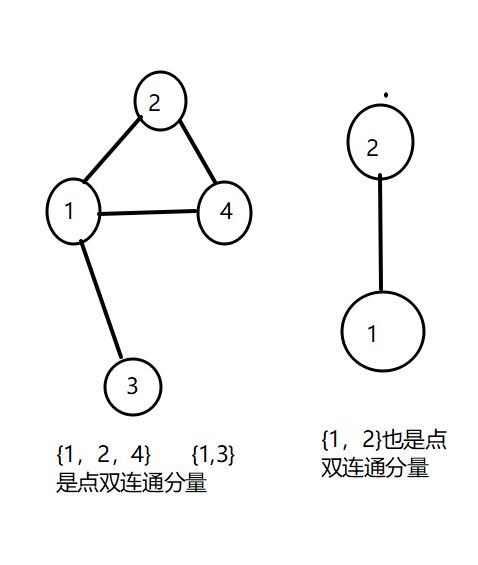
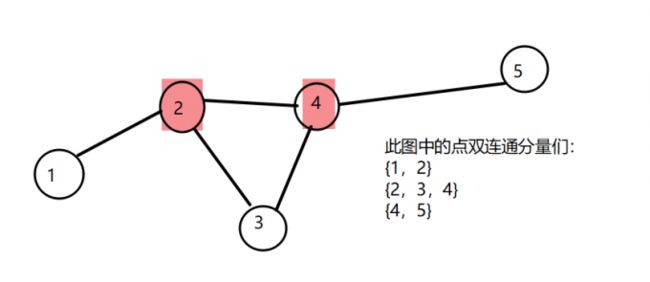
点双连通分量指：无向图中，分量中的任意两点间存在经过的点完全不相同的两条路径。

2.2 性质

割点起到类似“分割”的作用，分割两个点双连通分量。

一个割点最多出现在两个点双连通分量上，而非割点则最多出现在一个点双连通分量上。

注意到这一条性质后，其实点双连通分量的求解就不是一个难事了。一个点双连通分量最早会在割点或者图的根上被探测到。当\(tarjan\)找到一个割点后，将栈中的所有点和这个割点归纳到一个点双连通分量中。栈中的所有点弹出，但这个割点不弹出。

void tarjan(int u){
	DFN[u]=LOW[u]=++DFN[0]; sta[++top]=u; in[u]=true;
	int cnt=0;
	tor(i,u){
		int v=edge[i];
		if(!DFN[v]){
			cnt++;
			tarjan(v);
			LOW[u]=min(LOW[u],LOW[v]);
			if(LOW[v]>=DFN[u]){
				tot++;
				if(u!=root) ge[u]=true;
				while(sta[top]!=u){
					in[sta[top]]=false;
					lis[tot].push_back(sta[top]);
					top--;	
				}
				lis[tot].push_back(u);
			}
		}
		else if(in[v]) LOW[u]=min(LOW[u],DFN[v]);
	}
	if(u==root&&cnt>=2) ge[u]=true;
}

2.3 例题：[HNOI2012]矿场搭建

我是传送门

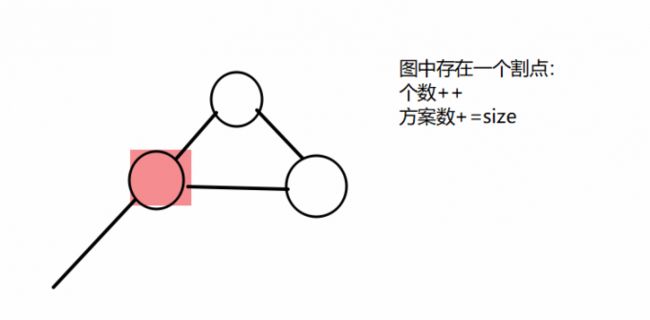
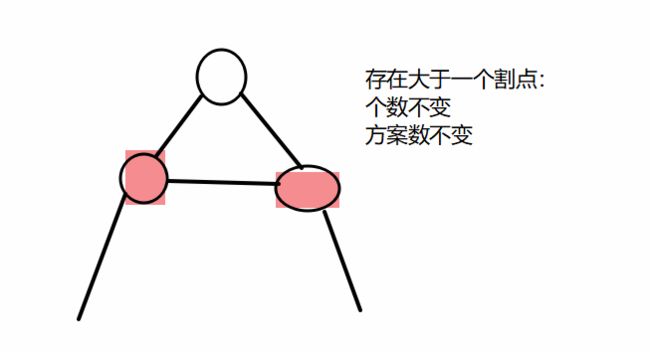
对图做一次点双连通分量的归纳，分情况讨论。

3.1 边双连通分量

边双连通分量：无向图中，分量中任意两点存在边完全不相同的两条路径。

边双连通分量就要有好理解很多，不同边双连通分量间被桥隔离。而求解方法也正是用\(tarjan\)求出桥后，跑一遍dfs之类的。

3.2 例题 [JSOI2012]越狱老虎桥

洛谷传送门

可以发现，可以被特工破坏掉的电网一定是图中桥。求出边双连通分量后，新图是一棵边集恰好是原图中桥的集合。将电网按权值排序，若此电网与之前的电网在一条链上则不能被割掉，否则输出答案。