Tarjan 算法及其应用

Tarjan 算法及其应用

NO.1 求强连通分量

学习链接： https://www.cnblogs.com/shadowland/p/5872257.html

学习心得： dfn[cur] 记录访问 cur 结点的时间戳，low[cur] 记录 cur 结点及其子树中时间戳最小是多少，严格意义上来讲low[cur]，记录的是在不回头遍历父节点的前提下第一次能访问到的最早的已遍历结点的时间戳。显然当访问 cur 结点的子节点 to 时，若 dfn[to] 不为0，则 to 结点到 cur 或 cur 的祖先结点中必然存在环，亦即到 to 结点为止的递归栈中的所有结点可以构成一个强连通分量。因为要先处理子节点后才能得出上层结点的 low，因此必然用后序遍历。具体的细节证明可参考链接。

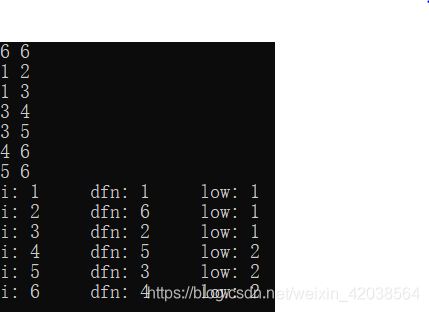
画张图解释下上述low严格意义上的含义。假设现在建无向边(加边时建正向反向各建一次边)，建边：6点、6条双向边
1 2
1 3
3 4
3 5
4 6
5 6

结果：遍历顺序1->3->5->6->4->(到3，回溯改4、6、5)->2,这里dfs序中3可看作4的虚子结点，即3在4、5、6的子树中，1、2不在。

代码实现：

#include 
#define ll long long
#define INF 0x3f3f3f3f
#define mem( f, x ) memset( f, x, sizeof( f ) )
#define pii pair
#define fi first
#define se second
#define mk(x, y) make_pair( x, y )
#define pk push_back
using namespace std;
const int M = 1e5 + 5;
const int N = 1e5 + 5;
int m, n, cnt, ck_num, col_num;
int head[N], dfn[N], low[N], color[N];
bool vis[N];
int sk[N], top;

struct eg{
    int to, pre;
    eg( ){ to = pre = 0; }
    eg( int tt, int pp ){
        to = tt, pre = pp;
    }
}e[2*M];

void add( int x, int y ){
    e[++cnt] = eg( y, head[x] );
    head[x] = cnt;
}

void Tarjan( int cur ){
    dfn[cur] = low[cur] = ++ck_num;
    vis[cur] = 1;
    sk[++top] = cur;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        if( !dfn[to] ){
            Tarjan( to ); //后序遍历
            low[cur] = min( low[cur], low[to] ); //根据子树更新当前结点中的low[cur]
        }
        else if( vis[to] )
            low[cur] = min( low[cur], dfn[to] ); //邻接结点在递归栈中时，根据邻接结点更新当前结点的low
                                                //(已遍历至终点，终点low可直接根据其已成为祖先的邻接结点的时间戳直接更新low)
    }
    if( dfn[cur] == low[cur] ){
        color[cur] = ++col_num;
        vis[cur] = 0; //cur结点出栈是一定要记得
        while( sk[top] != cur ){
            color[sk[top]] = col_num;
            vis[sk[top--]] = 0;
        }
        top--;
    }
}

void init( ){
    for( int i = 0; i <= n; i++ )
        head[i] = dnf[i] = low[i] = vis[i] = color[i] = 0;
    cnt = top = ck_num = col_num = 0;
}

int main( ){
    while( scanf( "%d %d", &n, &m ) != EOF ){
        init( );
        int x, y;
        for( int i = 0; i < m; i++ ){
            scanf( "%d %d", &x, &y );
            add( x, y ); //强连通针对无向图
        }
        for( int i = 1; i <= n; i++ )
            if( !dfn[i] )
                Tarjan( i );
        cout << "num: " << col_num << endl; //强连通分量数目
        for( int i = 1; i <= n; i++ ) //颜色相同的属于同一强连通分量
            cout << "i: " << i << "     color: " << color[i] << endl;
    }
    return 0;
}

NO.2 Tarjan缩点

学习网址： 内含Tarjan实现原理、缩点、割点、桥的具体说明
注： 链接网址原理讲解可作参考，代码实现有些瑕疵，代码不建议参考。

缩点过程： 属同一个强连通分量的点可以用一个超级点来代替，代码中表现为Tarjan实现过程中的上色数组color中所存的涂色点即为超级点。复杂图由此变一定可简化为一张有向无环图，对简化过的图进行处理就能省去很多麻烦。作为对比的是在无向图中也可利用并查集进行缩点，这里不做赘述。

例题附模板： HDU 2767
题意： 一张有向图，求整张图构成强连通分量至少要添几条有向边。
思路： 缩点后求每个超级点之间出度或入度为0的结点数，两者求最大值即可。

代码实现：

#include 
#define ll long long
#define mem( f, x ) memset( f, x, sizeof( f ) )
#define INF 0x3f3f3f3f
#define pii pair
#define mk( x, y ) make_pair
#define fi first
#define se second
#define pk push_back
using namespace std;
const int N = 20005;
const int M = 50005;
int m, n, cnt;
int head[N];
bool in[N], out[N];
int dfn[N], low[N], color[N], vis[N];
int sk[N], top;
int ck_num, col_num;

struct eg{
    int to, pre;
    eg( ):to(0), pre(0){ }
    eg( int tt, int pp ):to(tt), pre(pp){ }
}e[M];

void add( int x, int y ){
    e[++cnt] = eg( y, head[x] );
    head[x] = cnt;
}

void Tarjan( int cur ){
    dfn[cur] = low[cur] = ++ck_num;
    vis[cur] = 1;
    sk[++top] = cur;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        if( !dfn[to] ){
            Tarjan( to );
            low[cur] = min( low[cur], low[to] );
        }
        else if( vis[to] )
            low[cur] = min( low[cur], dfn[to] ); 
            //此处可写成low[cur] = min( low[cur], low[to] );
            //vis[to] = 1保证了cur和to同在递归栈中，属于同一强连通分量，	
            //因此low[cur]若要根据dfn[to]更新，
            //最终还是会更新成low[to]由于两者属同一强连通分量，
            //省略中间过程早些直接更新成low[to]没有影响
            //这里要和求割点和桥时做区分，后者的dfn[to]不能换成low[to]，
            //因为求桥或割点时的判别式不一定保证cur和to属同一强连通分量
    }
    if( dfn[cur] == low[cur] ){
        color[cur] = ++col_num;
        while( sk[top] != cur ){
            color[sk[top]] = col_num;
            vis[sk[top--]] = 0;
        }
        vis[sk[top]] = 0;
        top--;
    }
}

void init( ){
    for( int i = 0; i <= n; i++ )
        head[i] = in[i] = out[i] = dfn[i] = low[i] = vis[i] = color[i] = 0;
    cnt = ck_num = col_num = top = 0;
}

int main( ){
    int t;
    scanf( "%d", &t );
    mem( head, 0 );
    while( t-- ){
        scanf( "%d %d", &n, &m );
        init( );
        int x, y;
        for( int i = 0; i < m; i++ ){
            scanf( "%d %d", &x, &y );
            add( x, y );
        }
        for( int i = 1; i <= n; i++ )
            if( !dfn[i] )
                Tarjan( i );
        if( col_num == 1 ){
            printf( "0\n" );
            continue;
        }
        int in_num = col_num, out_num = col_num;

        for( int i = 1; i <= n; i++ ){
            for( int j = head[i]; j; j = e[j].pre ){
                int to = e[j].to;
                if( color[to] != color[i] ){
                    if( !in[color[to]] ){
                        in_num--;
                        in[color[to]] = 1;
                    }
                    if( !out[color[i]] ){
                        out_num--;
                        out[color[i]] = 1;
                    }
                }

            }
        }
        printf( "%d\n", max( in_num, out_num ) );
    }
    return 0;
}

NO.3 求割点

割点定义： 无向图中去掉某个点及其所关联边后，整张图的连通分量会增加。

割点判别： 假设当前结点为cur，判割点只需判断 cur 的子树结点中是否有不通过 cur 结点就无法回溯到 cur 的祖先(不包含cur) 的子结点。Tarjan 中可体现为cur 的子树中存在某个结点to，使得 low[to] >= dfn[cur]。需要注意的是这里的判别式是带等号的，因为若 to 最远只能回溯到当下判别点 cur，那也就是说当把 结点 cur 去除时 to 就和 cur 的祖先结点分离了，也就增加了连通分量数。这一点要与判 ” 桥 “ 时作区分，具体差别在第四部分求桥时再作详述。另外每次遍历时都是由根节点开始，我们无法判去除根节点时其子树的回溯情况，因此我们需要对根节点进行特判，当根节点的子节点数大于 1 时，去掉根节点必然会引起整张图强连通分量数的增加。

注： 割点是以无向图为前提，但在Tarjan中遍历不同于别的无向图 dfs 要利用 cur 的父节点阻止 cur 的邻接结点对 cur 结点回头重复遍历(因为建边时建的双向边)，Tarjan中的dfn[to] == 0已经保证了不会重复dfs，但需要强调的一点是遍历是不能像上述的记录父节点，遍历邻接结点时若是父节点直接continue掉，因为low[cur]不论to是否已遍历都需要根据dfn[to]进行修改，相反求桥的过程中子节点不能回去访问父节点后反向更新自己，因为桥同时涉及两端的点，若直接由根据双向边中刚刚经历过的父节点当作这一次的子结点to更新low，就默认两者之间的边存在，而判桥时的判别式中是不带等号的，此时更新将导致对于桥(u,v)，只要能回溯到v便一定能回溯到u，那就一定能取到等号，这会导致没有桥存在。

代码实现：

#include 
#define ll long long
#define INF 0x3f3f3f3f
#define mem( f, x ) memset( f, x, sizeof( f ) )
#define pii pair
#define fi first
#define se second
#define mk(x, y) make_pair( x, y )
#define pk push_back
using namespace std;
const int M = 1e5 + 5;
const int N = 1e5 + 5;
int m, n, cnt;
int dfn[N], low[N];
int head[N];
int ck_num;
bool cut[N];

struct eg{
    int to, pre;
    eg(){ to = pre = 0; }
    eg( int tt, int pp ){
        to = tt, pre = pp;
    }
}e[M<<1];

void add( int x, int y ){
    e[++cnt] = eg( y, head[x] );
    head[x] = cnt;
}

void init( ){
    for( int i = 0; i <= n; i++ )
        head[i] = cut[i] = dfn[i] = 0;
    cnt = ck_num = 0;
}

void dfs( int cur, int root ){
    dfn[cur] = low[cur] = ++ck_num;
    int ct = 0;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        ct++; //ct 只在cur == root时才有用，其他情况不会去判ct
        if( !dfn[to] ){ //保证了每个点只遍历一次
            dfs( to, root );
            low[cur] = min( low[cur], low[to] );
            if( cur != root && low[to] >= dfn[cur] ) cut[cur] = 1;
            if( cur == root && ct > 1 ) cut[cur] = 1;
        }
        else 
            low[cur] = min( low[cur], dfn[to] );
    }
}

int main( ){
    while( scanf( "%d %d", &n, &m ) != EOF ){
        int x, y;
        init( );
        for( int i = 0; i < m; i++ ){
            scanf( "%d %d", &x, &y );
            add( x, y );
            add( y, x );
        }
        for( int i = 1; i <= n; i++ ){
            if( !dfn[i] )
                dfs( i, i );
        }
        int tot = 0;
        for( int i = 1; i <= n; i++ )
            if( cut[i] )
                tot++;
        printf( "%d\n", tot );
        for( int i = 1; i <= n; i++ )
            if( cut[i] )
                printf( "%d ", i );
        printf( "\n" );
    }
    return 0;
}

NO.4 求桥(割边)

桥的定义： 无向图中去掉某条边后，整张图的连通分量会增加。
桥的判别： 假设当前结点为cur，当前遍历到的 cur 的邻接结点为to，我们需要判别的是边( cur, to )是否为桥，只需判断 cur 的子树结点中是否有不通过 cur 结点就无法回溯到 cur 及其祖先的子结点 (这里注意与判割点做区分，割点中是去掉 cur 后，cur的子树结点最多只能再次回溯到cur，无法进一步回溯到 cur 的祖先；而在判桥时，去掉 cur 后 cur的子树结点连cur都没办法回溯到。可以这么理解，边(cur，to)实际上属于to，若去掉这条边后，cur的子树结点仍能回溯到cur，则这条边存不存在就没区别了，因为cur必然又能回溯到cur的祖先，综上，桥的判别式为：low[to] > dfn[cur]，不取等号。记忆为 “歌曲可回头”，即求割点时需要取等号且求割点时即使有回头边也要根据前一次dfs的父节点更新子节点，这是求桥和割点时唯一的区别)。

例题： 洛谷 1656

代码实现：

#include 
#define ll long long
#define mem( f, x ) memset( f, x, sizeof( f ) )
#define pii pair
#define mk(x,y) make_pair(x, y)
#define pk push_back
#define fi first
#define se second
using namespace std;
const int M = 1e5 + 50;
const int N = 1e5 + 50;
int m, n;
int dfn[N], low[N], ck_num;
int head[N], cnt;
bool bridge[2*M];
pii ans[M];

struct eg{
    int to, pre;
    eg( ){ to = pre = 0;}
    eg( int tt, int pp ){
        to = tt, pre = pp;
    }
}e[2*M];

void add( int x, int y ){
    e[++cnt] = eg( y, head[x] );
    head[x] = cnt;
}

void init( ){
    for( int i = 0; i <= n; i++ )
        head[i] = dfn[i] = 0;
    for( int i = 0; i <= 2*m; i++ )
        bridge[i] = 0;
    ck_num = 0;
    //这里需要特别留意，边的编号cnt从2开始，1没有异或的对象
    //如2^1 = 3  3^1 = 2，则2与3为一对异或对象
    cnt = 1; 
}

void Tarjan( int cur, int fa ){
    dfn[cur] = low[cur] = ++ck_num;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        if( !dfn[to] ){
            Tarjan( to, cur );
            low[cur] = min( low[cur], low[to] );
            if( low[to] > dfn[cur] ) bridge[i] = bridge[i^1] = 1;
        }
        else if( to != fa ) //注意与求割点的区别，不可回头更新
            low[cur] = min( low[cur], dfn[to] );
    }
}

bool cmp( pii p1, pii p2 ){
    if( p1.fi == p2.fi )
        return p1.se < p2.se;
    return p1.fi < p2.fi;
}

int main( ){
    while( scanf( "%d %d", &n, &m ) != EOF ){
        init( );
        int x, y;
        for( int i = 0; i < m; i++ ){
            scanf( "%d %d", &x, &y );
            add( x, y );
            add( y, x );
        }
        for( int i = 1; i <= n; i++ )
            if( !dfn[i] )
                Tarjan( i, 0 );
        int tot = 0;
        for( int i = 2; i <= cnt; i += 2 )
            if( bridge[i] ){
                int x = e[i].to, y = e[i^1].to;
                if( x > y ) swap( x, y );
                ans[tot++] = mk( x, y );
            }
        sort( ans, ans+tot, cmp );
        for( int i = 0; i < tot; i++ )
            printf( "%d %d\n", ans[i].fi, ans[i].se );

    }
    return 0;
}

NO.5 求双连通分量

参考链接： 学习链接 可细读
      参考链接 看看性质，参考思想即可

双联通分量(DCC)： 可进一步分为 点双连通 和 边双连通，若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。一个无向图中的每一个极大点（边）双连通子图称作此无向图的点（边）双连通分量。

性质:

1. 任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性，即DCC中无割点
2. 若DCC间有公共点，则公共点为原图的割点
3. 无向连通图中割点一定属于至少两个DCC，非割点只属于一个DCC