概率统计总结

一、随机事件

概念

现实生活中，一个动作或一个事情，在一定条件下，所得到的结果是不能预先完全确定的，而只能确定是多种可能结果中的一种，称这种现象为随机事件。我们用$X$表示，用$p(X=x_i)$表示这个事件出现结果为$x_i$的概率（信念的度量），其中$x_i$为随机变量$X$出现的若干个结果中的第$i$个。

条件概率

研究随机事件之间关系时，在已知某些事件$X$的条件下考虑另一些事件$Y$发生的概率是经常遇到的,即为条件概率$p(Y|X)$。
$$P(Y=y_i|X=x_i)=\frac{P(X_{x_i}{Y}_{y_i})}{P(X_{x_i})}$$

二、随机变量

随机变量及其分布

描述随机变量时不仅要说明它能够取哪些值，而且还要关心它取这些值的概率，即为随机变量的分布，分为离散型随机变量和连续性随机变量。

$$P\{X=x_k\}=p_k,k=1,2,...$$
$$F(x)=P\{X<=x\},x\in (-\infty ,+\infty )$$

随机变量的特征

数学期望

• 离散型：
  $$E(X)=\sum _i{x}_i{p}_i$$
• 连续型
  $$E(X)={\int }_{-\infty }^{+\infty }xf（x）dx$$

方差

• 离散型
  $$D（X）=E\{[X-E(X){]}^2\}$$
• 连续型
  $$D（X）={\int }_{-\infty }^{+\infty }(x-E(X){)}^{2}f（x）dx$$

协方差

$$Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}$$

• 上面的公式适合离散型和连续型

相关系数(皮尔逊系数)

$$\rho （X,Y）=\frac{Cov(X，Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$- 衡量两个变量之间的相关程度。相关系数在-1到1之间，小于0表示负相关，大于0表示正相关。绝对值$|\rho （X,Y）|$ 表示相关度的大小。越接近1，相关度越大。

三、数理统计

概念

在数理统计中，称研究对象的全体为总体，通常用一个随机变量表示总体。组成总体的每个基本单元叫个体。从总体 $X$ 中随机抽取一部分个体 $X_1,X_2,...,X_n$ ,称 $X_1,X_2,...,X_n$ 为取自 $X$ 的容量为 $n$ 的样本（这里的$X_1$是表示第一次随机试验它的取值有$i$个用$x_i$表示对应的结果，即为观测值）

统计量与抽样

数理统计的任务是采集和处理带有随机影响的数据，或者说收集样本并对之进行加工，对样本的研究推断总体（对总体得出一定的结论），这一过程称为为统计推断。在统计推断中，对样本进行加工整理，实际上就是根据样本计算出一些量，使得这些量能够将所研究问题的信息集中起来。这种根据样本计算出的量就是下面将要定义的统计量，因此，统计量是样本的某种函数

常用的统计量

1. 样本均值

设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，称
$$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$$
为样本均值。通常用样本均值来估计总体分布的均值和对有关总体分布均值的假设作检验。

2. 样本方差

设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，$\overline{X}$ 为样本均值，称
$$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2$$
为样本方差。通常用样本方差来估计总体分布的方差和对有关总体分布均值或方差的假设作检验。

3. $k$阶样本原点矩

设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，称
$$A_k=\frac{1}{n}\sum _{i=1}^n{X}_i^k$$
为样本的 $k$ 阶原点矩（可以看到 $k=1$ 时，相当于样本均值），通常用样本的无阶原点矩来估计总体分布的 $k$ 阶原点矩。

4. $k$ 阶样本中心矩

设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，$\overline{X}$ 为样本均值，称
$$M_k=\frac{1}{n}\sum _{i=1}^n(X_i-\overline{X}{)}^k$$
为样本的 $k$ 阶中心矩，通常用样本的 $k$ 阶中心矩来估计总体分布的 $k$ 阶中心矩。

其实当样本量足够大时，$1/n$ 与 $1/(n-1)$ 近似于相等

5. 顺序统计量

设 $X_1,X_2,...,X_n$ 是抽自总体 $X$ 的样本，$x_1,x_2,...，x_n$ 为样本观测值。将 $x_1,x_2,...，x_n$ 按照从小到大的顺序排列为
$$x_{（1）}<=x_{（2）}<=...<=x_{（n）}$$
当样本 $X_1,X_2,...,X_n$ 取值 $x_1,x_2,...，x_n$ 时，定义 $X_{(k)}$ 取值 $X_{(k)}（k=1,2，...,n）$，称 $X_{（1）},X_{（2）},...,X_{（n）}$ 为 $X_1,X_2,...,X_n$ 的顺序统计量。

显然，$X_{（1）}=min{X}_i$ 是样本观察中最小的一个，称为最小顺序统计量。$X_{（n）}=max{X}_i$ 是样本观测值中取值最大的一个，成为最大顺序统计量。称$X_{（r）}$ 为第 $r$ 个顺序统计量。

四、描述性统计

数据集中趋势的度量

• 平均数、中位数、众数、百分位数、频数

数据离散趋势的度量

• 方差、标准差、极差、变异系数、四分位数、偏度、峰度
• 变异系数：
  • 是刻画数据相对分散性的一种度量。变异系数只在平均值不为零时有定义，而且一般适用于平均值大于零的情况。变异系数$cv=\frac{S}{\overline{X}}$ 也被称为标准离差率或单位风险。
  • 当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，变异系数可以消除测量尺度和量纲的影响。

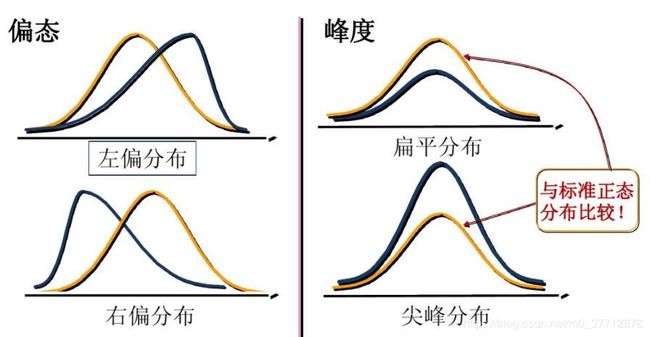
偏度与峰度

偏度（skewness）：也称为偏态，是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。直观看来就是密度函数曲线尾部的相对长度。**偏度刻画的是分布函数（数据）的对称性。**关于均值对称的数据其偏度系数为0，右侧更分散的数据偏度系数为正，左侧更分散的数据偏度系数为负。

1. 正态分布的偏度为0，两侧尾部长度对称。
2. 左偏:

• 若以bs表示偏度。bs<0称分布具有负偏离，也称左偏态；
• 此时数据位于均值左边的比位于右边的少，直观表现为左边的尾部相对于与右边的尾部要长；
• 因为有少数变量值很小，使曲线左侧尾部拖得很长；

3.右偏：

• bs>0称分布具有正偏离，也称右偏态；
• 此时数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于与左边的尾部要长；
• 因为有少数变量值很大，使曲线右侧尾部拖得很长；

峰度（peakedness;kurtosis）： 说明的是分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量，如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然。峰度刻画的是分布函数的集中和分散程度

• 偏度计算公式
  $$g_1=\frac{n(n+1)}{(n-1)(n-2)(n-3)s^4}\sum _{i=1}^n(x_i-\overline{x}{)}^3$$
• 峰度计算公式
  $$g_1=\frac{n(n+1)}{(n-1)(n-2)(n-3)s^4}\sum _{i=1}^n(x_i-\overline{x}{)}^4-3\frac{(n-1{)}^2}{(n-2)(n-3)}$$

五、常见分布

离散型

N重伯努利分布

$$P\{X=k\}=C_n^k{p}^k(1-p{)}^{n-k}$$

• 记为$X\sim B(n,p)$

泊松分布（Poisson distribution）

泊松分布是用来描述泊松试验的一种分布，满足以下两个特征的试验可以认为是泊松试验：

• 所考察的事件在任意两个长度相等的区间里发生一次的机会均等
• 所考察的事件在任何一个区间里发生与否和在其他区间里发生与否没有相互影响，即是独立的

泊松分布需要满足一些条件：

• 试验次数n趋向于无穷大
• 单次事件发生的概率p趋向于0
• np是一个有限的数值

泊松分布的一些例子：

• 一定时间段内，某航空公司接到的订票电话数
• 一定时间内，到车站等候公交汽车的人数
• 一匹布上发现的瑕疵点的个数
• 一定页数的书刊上出现的错别字个数

一个服从泊松分布的随机变量X，在具有比率参数（rate parameter）$\lambda$ （$\lambda =np$）的一段固定时间间隔内，事件发生次数为i的概率为
$$P\{X=k\}=\frac{{\lambda }^k}{k!}{e}^{-\lambda }$$

• 记为$X\sim P(\lambda )$

• 二项分布，泊松分布，正态分布的关系
  这三个分布之间具有非常微妙的关联。当n很大，p很小时，如n ≥ 100 and np ≤ 10时，二项分布可以近似为泊松分布。当λ很大时，如λ≥1000时，泊松分布可以近似为正态分布。当n很大时，np和n(1-p)都足够大时，如n ≥ 100 , np ≥10，n(1-p) ≥10时，二项分布可以近似为正态分布。

几何分布（Geometric distribution）

考虑独立重复试验，几何分布描述的是经过k次试验才首次获得成功的概率，假定每次成功率为p，
$$P\{X=n\}={(1-p)}^{n-1}p$$

负二项分布（Negative binomial distribution）

考虑独立重复试验，负二项分布描述的是试验一直进行到成功r次的概率，假定每次成功率为p，
$$P\{X=n\}=C_{n-1}^{r-1}{p}^r{(1-p)}^{n-r}$$

超几何分布（Hypergeometric Distribution）

超几何分布描述的是在一个总数为N的总体中进行有放回地抽样，其中在总体中k个元素属于一组，剩余N-k个元素属于另一组，假定从总体中抽取n次，其中包含x个第一组的概率为
$$P\{X=n\}=\frac{C_k^x{C}_{N-k}^{n-x}}{C_N^n}$$

连续型

均匀分布 （Uniform distribution）

均匀分布指的是一类在定义域内概率密度函数处处相等的统计分布。

若X是服从区间[a,b]上的均匀分布，则记作$X\sim U[a,b]$

均匀分布X的概率密度函数为

$$f(x)=\{\begin{array}{ll}\frac{1}{b-a},& a\le x\le b\\ 0,& others\end{array}$$

分布函数为
$$F(x)=\{\begin{array}{ll}0,& x<a\\ (x-a)(b-a),& a\le x\le b\\ 1,& x>b\end{array}$$
均匀分布的一些例子：

• 一个理想的随机数生成器
• 一个理想的圆盘以一定力度旋转后静止时的角度

正态分布 （Normal distribution）

正态分布，也叫做高斯分布，是最为常见的统计分布之一，是一种对称的分布，概率密度呈现钟摆的形状，其概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(x-u{)}^2}{2{\sigma }^2}}$$
记为$X\sim N(\mu ,{\sigma }^2)$ , 其中μ为正态分布的均值，σ为正态分布的标准差

有了一般正态分布后，可以通过公式变换将其转变为标准正态分布 Z ~ N(0,1)，
$$Z=\frac{X-\mu }{\sigma }$$
正态分布的一些例子：

• 成人的身高
• 不同方向的气体分子的运动速度
• 测量物体质量时的误差

正态分布在现实生活有着非常多的例子，这一点可以从中心极限定理来解释，中心极限定理说的是一组独立同分布的随机样本的平均值近似为正态分布，无论随机变量的总体符合何种分布。

指数分布 （Exponential distribution）

指数分布通常被广泛用在描述一个特定事件发生所需要的时间，在指数分布随机变量的分布中，有着很少的大数值和非常多的小数值。

指数分布的概率密度函数为
$$f(x)=\{\begin{array}{ll}\lambda e^{-\lambda x},& x\ge 0\\ 0,& x<0\end{array}$$
记为 $X\sim E（\lambda )$, 其中λ被称为率参数（rate parameter），表示每单位时间发生该事件的次数。

分布函数为
$$F(a)=P\{X\le a\}=1-e^{-\lambda a},a\ge 0$$
指数分布的一些例子：

• 顾客到达一家店铺的时间间隔
• 从现在开始到发生地震的时间间隔
• 在产线上收到一个问题产品的时间间隔

关于指数分布还有一个有趣的性质的是指数分布是无记忆性的，假定在等候事件发生的过程中已经过了一些时间，此时距离下一次事件发生的时间间隔的分布情况和最开始是完全一样的，就好像中间等候的那一段时间完全没有发生一样，也不会对结果有任何影响，用数学语言来表述是
$$P\{X>s+t|X>t\}=P\{X>s\}$$

$\Gamma$分布

• 常用来描述某个事件总共要发生n次的等待时间的分布
• 假设$X_1,X_2,...X_n$为连续发生事件的等候时间，且这n次等候时间为独立的，那么这$n$次等候时间之和$Y(Y=X_1+X_2+...+X_n)$服从伽玛分布，即 $Y\sim \Gamma (\alpha ,\beta )$，其中$\alpha =n$, $\beta =\lambda$。这里的 $\lambda$ 是连续发生事件的平均发生频率。
  指数分布是伽玛分布$\alpha$ = 1的特殊情况。
  令$X\sim \Gamma (\alpha ,\beta )$，且令$\lambda =\beta$
  （即$X\sim \Gamma (\alpha ,\lambda )$），則：

$$f\left(x\right)=\frac{x^{(\alpha -1)}{\lambda }^{\alpha }{e}^{(-\lambda x)}}{\Gamma \left(\alpha \right)}$$

其中Gamma函数特征为：

$$\{\begin{array}{ll}\Gamma (\alpha )=(\alpha -1)!,& if\alpha is{\mathbb{Z}}^{+}\\ \Gamma (\alpha )=(\alpha -1)\Gamma (\alpha -1),& if\alpha is{\mathbb{R}}^{+}\\ \Gamma \left(\frac{1}{2}\right)=\sqrt{\pi }& \end{array}$$

威布尔分布 （Weibull distribution）

常用来描述在工程领域中某类具有“最弱链”对象的寿命

三个常用的抽样分布

• ${\chi }^2$分布、$t$分布、$F$分布

${\chi }^2$分布

若$k$个随机变量$Z_1$、……、$Z_k$是相互独立，符合标准正态分布的随机变量（数学期望为0、方差为1），则随机变量$Z$的平方和
$$X=\sum _{i=1}^k{Z}_i^2$$
被称为服从自由度为 $k$ 的${\chi }^2$分布，记作$X\sim {\chi }^2(k)$或者$X\sim {\chi }_k^2$

• 概率密度函数为：
  $$f_k(x)=\frac{{\frac{1}{2}}^{\frac{k}{2}}}{\Gamma (\frac{k}{2})}{x}^{\frac{k}{2}-1}{e}^{\frac{-x}{2}}$$
  其中x≥0，当x≤0时$f_k(x)=0$

$t$分布

设$X\sim N(0,1)$,$Y\sim {\chi }^2$且$X,Y$相互独立，则称的随机变量$T=\frac{X}{\sqrt{Y/\nu }}\sim t(\nu )$,$\nu$为自由度。

• 概率密度函数：
  $$f(t)=\frac{\Gamma (\frac{\nu +1}{2})}{\sqrt{\nu \pi }\Gamma (\frac{\nu }{2})}(1+\frac{t^2}{\nu }{)}^{\frac{-(\nu +1)}{2}}$$

参数$\nu$为自由度。$\Gamma$是伽玛函数。

$F$分布

一个$F$分布的随机变量是两个${\chi }^2$分布变量除以自由度的比率：
$$F(d_1,d_2)=\frac{U_1/d_1}{U_2/d_2}=\frac{U_1/U_2}{d_1/d_2}$$

其中：

• U₁和U₂呈卡方分布，它们的自由（degree of freedom）分别是d₁和d₂。
• U₁和U₂是相互独立的。

正态总体下的抽样分布

一个正态分布总体

• $\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$,标准化得$\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$
• $\frac{1}{{\sigma }^2}{\sum }_{i=1}^n(X_i-\mu {)}^2\sim {\chi }^2(n)$
• $\frac{1}{{\sigma }^2}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2=\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$
• $\overline{X}$与$S^2$相互独立
• $E(S^2)={\sigma }^2$
• $\frac{\overline{X}-\mu }{S/\sqrt{n}}\sim t(n-1)$ ,这就是我们常用的t检验

两个正态分布总体

常见的分布汇总

六、参数估计

概念

利用样本的统计数字特征（均值、标准差）去估计总体的概率分布参数，参数估计分为，点估计和区间估计。

点估计

• 点估计的评价标准，无偏性、有效性、一致性
• 估计方法，矩估计、极大似然法

区间估计

• 利用正态分布、$t$分布、${\chi }^2$分布去估计区间

七、假设检验

概念

• 假设检验问题时统计推断中的一类重要问题，在总体的分布函数完全未知或只知其形式，不知其参数的情况，为了推断总体的某些未知特性，提出某些关于总体的假设，这类问题被称为假设检验。
• 假设检验是基于小概率思想。即小概率事件在试验过程中不会发生，若试验过程中小概率事件发生了则被视为不合理，对于充分小的数$\alpha$,若一个事件的发生的概率不超过$\alpha$,这样的事件即为小概率事件，其中$\alpha$称为显著性水平

步骤

一个假设检验问题可以分为5步，无论细节如果变化，都一定会遵循这5个步骤。

1. 陈述研究假设，包含原假设（null hypothesis）和备择假设（alternate hypothesis）
2. 为验证假设收集数据
3. 构造合适的统计测试量并测试
4. 决定是接受还是拒绝原假设
5. 展示结论

步骤1：

通常来说，我们会把原假设的描述写成变量之间不存在某种差异，或不存在某种关联，备择假设则为存在某种差异或关联。

例如，原假设：男人和女人的平均身高没有差别， 备择假设男人和女人的平均身高存在显著差别。

步骤2:

为了统计检验的结果真实可靠，需要根据实际的假设命题从总体中抽取样本，要求抽样的数据要具有代表性，例如在上述男女平均身高的命题中，抽取的样本要能覆盖到各类社会阶级，各个国家等所有可能影响到身高的因素。

步骤3：

统计检验量有很多种类，但是所有的统计检验都是基于组内方差和组间方差的比较，如果组间方差足够大，使得不同组之间几乎没有重叠，那么统计量会反映出一个非常小的P值，意味着不同组之间的差异不可能是由偶然性导致的。

步骤4：

基于统计量的结果做出接受或拒绝原假设的判断，通常我们会以P=0.05作为临界值（单侧检验）。

步骤5：

展示结论。

统计量的选择

选择合适的统计量是进行假设检验的关键步骤，最常用的统计检验包括回归检验(regression test)，比较检验(comparison test)和关联检验(correlation test)三类。

回归检验

回归检验适用于预测变量是数值型的情况，根据预测变量的数量和结果变量的类型又分为以下几种。

	预测变量	结果变量
简单线性回归	单个，连续数值	连续数值
多重线性回归	多个，连续数值	连续数值
Logistic回归	连续数值	二元类别

比较检验

比较检验适用于预测变量是类别型，结果变量是数值型的情况，根据预测变量的分组数量和结果变量的数量又可以分为以下几种。

	预测变量	结果变量
Paired t-test	两组，类别	组来自同一总体，数值
Independent t-test	两组，类别	组来自不同总体，数值
ANOVA	两组及以上，类别	单个，数值
MANOVA	两组及以上，类别	两个及以上，数值

关联检验

关联检验常用的只有卡方检验一种，适用于预测变量和结果变量均为类别型的情况。

非参数检验

此外，由于一般来说上述参数检验都需满足一些前提条件，样本之间独立，不同组的组内方差近似和数据满足正态性，所以当这些条件不满足的时候，我们可以尝试用非参数检验来代替参数检验。

非参数检验	用于替代的参数检验
Spearman	回归和关联检验
Sign test	T-test
Kruskal–Wallis	ANOVA
ANOSIM	MANOVA
Wilcoxon Rank-Sum test	Independent t-test
Wilcoxon Signed-rank test	Paired t-test

两类错误

事实上当我们进行假设检验的过程中是存在犯错误的可能的，并且理论上来说错误是无法完全避免的。根据定义，错误分为两类，一类错误（type I error）和二类错误（type II error）。

• 一类错误：拒绝真的原假设

• 二类错误：接受错误的原假设

一类错误可以通过α值来控制，在假设检验中选择的 α（显著性水平）对一类错误有着直接影响。α可以认为是我们犯一类错误的最大可能性。以95%的置信水平为例，a=0.05，这意味着我们拒绝一个真的原假设的可能性是5%。从长期来看，每做20次假设检验会有一次犯一类错误的事件发生。

二类错误通常是由小样本或高样本方差导致的，二类错误的概率可以用β来表示，和一类错误不同的是，此类错误是不能通过设置一个错误率来直接控制的。对于二类错误，可以从功效的角度来估计，首先进行功效分析（power analysis）计算出功效值1-β，进而得到二类错误的估计值β。

一般来说这两类错误是无法同时降低的，在降低犯一类错误的前提下会增加犯二类错误的可能性，在实际案例中如何平衡这两类错误取决于我们更能接受一类错误还是二类错误。

八、方差分析

思想

• 数据驱动应用中，时常出现A/B测试，经常需要验证新方案B相对于A（原方案）是否具有显著性提升（或降低）。研究分类变量作为自变量时对于因变量是否具有显著性

• 那么，如何衡量显著性？基于组间方差和组内方差对比！

• 组间方差
  $$S_b=\frac{{\sum }_{i=1}^k{n}_i({\overline{X}}_i-\overline{X}{)}^2}{k-1}$$

• 组内方差

$$S_w=\frac{{\sum }_{i=1}^k{\sum }_{j=1}^{n_i}(x_{i,j}-{\overline{X}}_i{)}^2}{{\sum }_{i=1}^k{n}_i-k}$$

• 注：$k$为类别数，$n_i$为第$i$类的样本数量，${\overline{X}}_i$为第$i$类样本均值
• 构造随机变量$Z=\sqrt{S_b/S_w}\sim F(k,{\sum }_{i=1}^k{n}_i-k+1)$分布