数学模型之最小二乘法
前言废话
前面讲了线性回归分析,从观测数据中确定线性回归的模型的方法就是最小二乘法。即
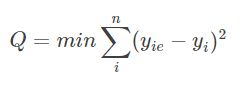
使得上面的均方误差和最小。(关于为什么,请参照以下博客)
如何理解最小二乘法?
本文将主要分析最小二乘法的具体解法。
关于最小二乘法的解法,一般由以下解法:
1、多元函数求最值(也有的说法把这当成最小二乘法)
2、利用线代的几何意义
3、梯度下降法
一、多元函数求最值
从本质上来说,上述均方误差和就是一个关于参数(a,b)的多元函数。如下图所示:

这里的f(xi)是线性回归模型ax+b。
对于多元函数来说,求其最小值,我们可以利用高等数学中多元函数求偏导的方式。即
解上述方程,就可以得到最终的β0,β1解。如下所示。(有凸函数理论可以证明,对于线性回归来说,其均方误差是有最小值,此处求得的β0,β1解就是其全局最优解,但是这条理论对其他回归模型可能不成立)。
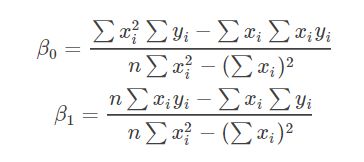
多元线性回归模型求解同理。
二、利用线代的几何意义
对于线性回归问题,我们可以换一个思路。即观测到一系列数据点,而这些数据点需要都在一条直线方程上。我们利用线性代数中解线性方程组的方式来解释最小二乘法。
为了简单叙述,
以y=cX1+dX2这个二元线性方程为例。(其中c、d是参数,X1,X2为自变量)
如题:观测到数据点(4 -1 5)、(2 2 10)、(0 0 1). 其中前两个是自变量X1、X2,最后一个是因变量y。
需要是上述数据点符合二元线性方程。即
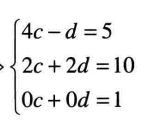
成立。
上述方程称为超定方程组,这种方程组并没有精确解(c、d)。我们需要需要求得一个近似解。
由线性代数的知识可以知道,上述方程组问题可以看成以下两个向量w、v的线性组合是否可以组合成b向量(此处应该是更好的写法应该是转置,但是比较难打,敬请见谅)
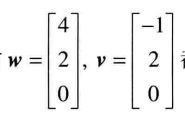
![]()
此时,向量w和v都在xy平面上,所以w、v的线性组合决不能跑到xy平面。而由于向量b的第三个值为1,它脱离了xy平面,所以此此w、v的线性组合是无法成为b向量的。这也验证了上述线性方程组无解的情况。如下图所示。
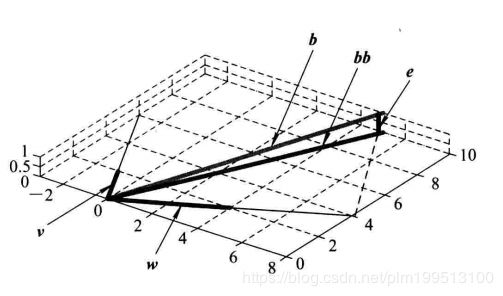
我们现在不要求w、v的合成向量
![]()
准确等于b,只希望使bb尽可能的接近b。我们知道,bb的可取范围是整个xy平面(w和v所有线性组合的平面),其中哪一点与向量b的矢量端最接近呢?应该是从b端向wv平面做垂线的垂足。此时两者的误差e就是垂线的长度,它也是平面上所有可能的bb中与b最小的误差。
那么如何确定e呢?很简单,确定向量e的条件就是它与v和w都正交,即

(好吧,我承认这是《使用大众线性代数》里面的内容,我不想手打了。我还没吃饭呢。┭┮﹏┭┮)
这里要说明一点,利用多元函数求最值和这里线代的几何意义求得的最值本质上是相同的。只需把前者的过程化成矩阵的形式即可。
三、梯度下降法
所谓梯度下降法,是迭代法计算最值的一种形式。是通过不断求导改变待求参数的值,来达到不断求得最值的过程。
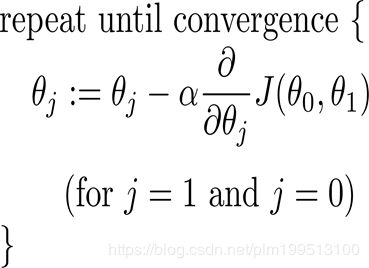
如上图所示,可以把这里的J(x,y)当成我们讨论的均方误差和。(其实这里J(x,y)是机器学习中的代价函数)
α是下降速度,可以根据现实情况选择(机器学习中时也叫做学习速率)。
对于一元线性回归来说就是下面这张图。
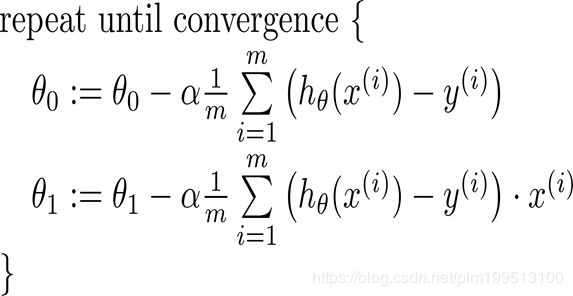
一般来说,梯度下降法可能会下降到局部最优点,但是对于线性回归来说其均方差函数大概是下面这个样子。
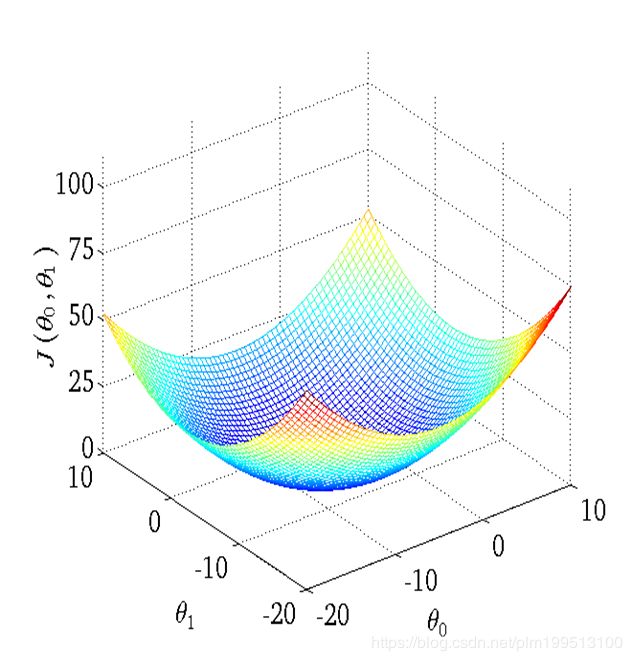
所以局部最优就是全局最优了。
这种算法不是这里的重点,值简要介绍到这儿。具体的其他性质,请自行查阅。
四、一个小实验
最后上一个用matlab做的一个小实验,进行线性回归的实验。
clear;
clc;
data_mat = load('ex0.txt');%从ex0.txt文本文件中读取数据
x = data_mat(:,2); %获取第二列数据,作为输入
y = data_mat(:,3); %获取第三列数据,作为输出
X = [data_mat(:,1:2)];%取出m行2列的系数矩阵,其中第一列全为1
w = pinv(A)*y;%计算获得回归参数a,b。其中pinv为伪逆函数
%构造数据,画出散点图和拟合图像
x1 = linspace(0,1,20);
y1 = w(1)*x1+w(2);
scatter(x,y),hold on, plot(x1,y1)
具体的数据和代码已经上传到对应的资源页了。