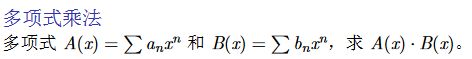【FFT快速傅里叶变换】讲解
参考来源:
十分简明易懂的FFT(快速傅里叶变换)
小学生都能看懂的FFT!!!
一、FFT的介绍
-
FFT是什么
快速傅里叶变换(FFT)是一种能在 O ( n log n ) O(n\log{n}) O(nlogn) 的时间内将一个多项式转换成它的点值表示的算法。 -
FFT的作用
快速计算多项式乘法(即卷积)
(还可以用到字符串的模糊匹配)前置知识
- 实际上就是把多项式看成一个函数,放到直角坐标系里。
- 这条曲线上就有无数个点,取n个不同的x带入,会得到n个不同的y,他们在坐标系中,就是n个不同的在这条曲线上的点。
- 也就是说,这n个点唯一确定这个多项式。 (为什么唯一确定呢?)
- 因为:把这n个x,y带入多项式,得到n个式子,把这n个式子联立起来,得到一个有n条方程的n元方程组,就可以求得每一项的系数(高斯消元法)。这样就唯一确定了一个多项式。
- 多项式乘法
-
系数表示的多项式乘法【 O ( n 2 ) O(n2) O(n2)】:枚举A(x)中的每一项,分别与B(x)中的每一项相乘,求得新的多项式C(x)。
-
点值表示的多项式乘法【 O ( n ) O(n) O(n)】: C ( x i ) = A ( x i ) × B ( x i ) C(xi)=A(xi)×B(xi) C(xi)=A(xi)×B(xi)。
-
那么我们要计算多项式的乘法,就可以先将系数表示转换为点值表示,相乘以后,再将点值表示转换为系数表示即可。——这个转换过程就用到了FFT。
-
朴素:系数转点值的算法叫DFT(离散傅里叶变换)
-
朴素:点值转系数叫IDFT(离散傅里叶逆变换)
二、DFT(离散傅里叶变换:系数表示 —> 点值表示)
- 复数知识回顾
- 复数可以看做复平面直角坐标系上的一个点(也可以是向量)。
x轴就是实数集的坐标轴,y轴就是虚数单位i轴 - 复数z的模定义为它到原点的距离,记为 ∣ z ∣ = ( a 2 + b 2 ) ∣z∣=\sqrt{(a^2 + b^2)} ∣z∣=(a2+b2)
- 复数z=a+bi的共轭复数为 a − b i a−bi a−bi(虚部取反)
- 复数运算
z 1 + z 2 = ( a + c ) + ( b + d ) i z1+z2=(a+c)+(b+d)i z1+z2=(a+c)+(b+d)i
z 1 z 2 = ( a c − b d ) + ( a d + b c ) i z1z2=(ac−bd)+(ad+bc)i z1z2=(ac−bd)+(ad+bc)i
( a 1 , θ 1 ) ∗ ( a 2 , θ 2 ) = ( a 1 a 2 , θ 1 + θ 2 ) — — 模 长 相 乘 , 极 角 相 加 (a1,θ1)∗(a2,θ2)=(a1a2,θ1+θ2) —— 模长相乘,极角相加 (a1,θ1)∗(a2,θ2)=(a1a2,θ1+θ2)——模长相乘,极角相加
- 离散傅里叶变换的思考
- 从这里开始所有的n都默认为2的整数次幂(虽然我不知道有什么用,但是大家都这样写了emmm,好像是为了保证每次分治时,不会出现奇数的长度)。
- 由上面的知识可知,系数表示 —> 点值表示,只需要带入n个x,求得n个点,就可以得到点值表示了。但是这n个点不是随意带入的,因为暴力计算 x k 0 , . . . , x k n − 1 x^0_k,... ,x^{n-1}_k xk0,...,xkn−1 也很费时间。
- 如果我们带入的这个x,能够使得 x k = ± 1 , ∀ k x^k=\pm1,\forall k xk=±1,∀k ,那么我们就不用计算 x k n − 1 x^{n-1}_k xkn−1了。
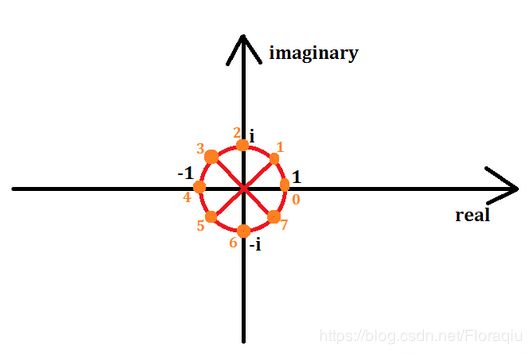
- 显然,复平面直角坐标系的单位圆上的每一个点都可以做到。
- 单位根
-
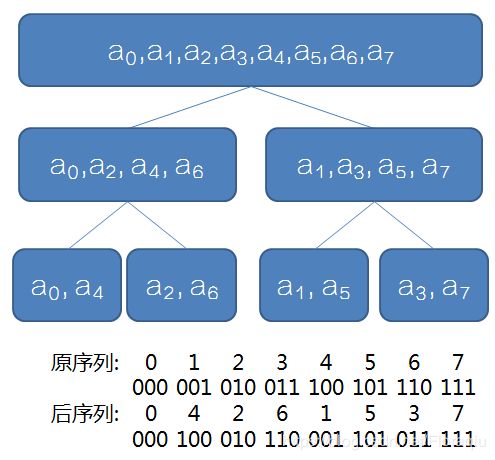
如果将单位圆等分为8等分,则橙色点即为n=8时要取的点,从(1,0)点开始,逆时针从0号开始标号,标到7号。
 (
(这个图是我偷的) -
记编号为k的点代表的复数值为 ω n k ω^k_n ωnk,那么由模长相乘,极角相加可知 ( ω n 1 ) k = ω n k (ω^1_n)^k=ω^k_n (ωn1)k=ωnk
-
其中 ω n 1 ω^1_n ωn1称为n次单位根,而且每一个ω都可以求出为
ω n k = cos k n 2 π + i sin k n 2 π ω^k_n=\cos{\frac{k}{n}2π}+i\sin{\frac{k}{n}2π} ωnk=cosnk2π+isinnk2π -
那么 ω n 0 , ω n 1 , . . . , ω n n − 1 ω^0_n,ω^1_n,...,ω^{n−1}_n ωn0,ωn1,...,ωnn−1即为我们要代入的 x 0 , x 1 , . . . , x n − 1 x^0,x^1,...,x^{n−1} x0,x1,...,xn−1。
-
单位根的性质
1、 ω n k = ω 2 n 2 k ω_n^k=ω_{2n}^{2k} ωnk=ω2n2k
它们表示的点(或向量)表示的复数是相同的。
2、 ω n k + n 2 = − ω n k ω_n^{k+\frac{n}{2}}=−ω_n^k ωnk+2n=−ωnk
它们表示的点关于原点对称,所表示的复数实部相反,所表示的向量等大反向。
3、 ω n 0 = ω n n ω_n^0=ω_n^n ωn0=ωnn
证明:把系数带到三角函数表达式中即可证明。
三、FFT(快速傅里叶变换:系数表示 —> 点值表示)
DFT 分治 --> FFT
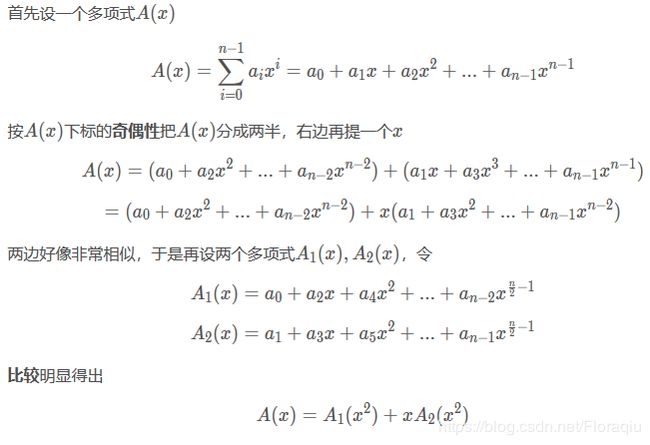
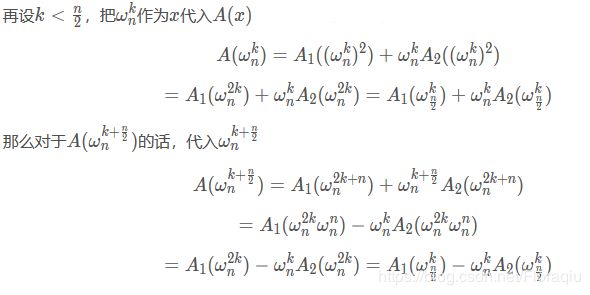
那么如果可以求出 A 1 ( ω n k ) A1(ω_n^k) A1(ωnk)和 A 2 ( ω n k ) A2(ω^k_n) A2(ωnk)的值,我们就可以求出 A ( ω n k ) A(ω_n^k) A(ωnk)和 A ( ω n k + n 2 ) A(ω^{k + \frac{n}{2}}_n) A(ωnk+2n)的值( k < n 2 k< \frac{n}{2} k<2n),也就是知道 A ( ω n i ) A(ω_n^i) A(ωni)( 0 < = i < n 0 <= i< n 0<=i<n)的值了。
-
分治边界是n=1,直接return。
-
分治的复杂度:
T ( n ) = 2 T ( n 2 ) + O ( n ) = O ( n log n ) T(n) = 2T(\frac{n}{2}) + O(n)= O(n\log{n}) T(n)=2T(2n)+O(n)=O(nlogn)
四、IFFT(快速傅里叶逆变换:点值表示 —> 系数表示)
- 结论: 一个多项式在分治的过程中乘上单位根的共轭复数,分治完的每一项除以n即为原多项式的每一项系数。
- 也就是说 FFT 和 IFFT 可以用几乎同样的方式一起求,只不过IFFT带入前,需要求一次倒数(即共轭复数),最后的系数还需要除以n,其他的求法都一样。
五、代码实现(主要看思路)
以下板子都是我抄的,没有测试过,看个思路就可以了。
1、递归版
#include- 可以发现每个位置分治后的最终位置为其二进制翻转后得到的位置。
- 那么如何快速求一个数的二进制翻转呢?
- 我们 可以用递归的思路来考虑。
- 我们可以把一个二进制数看成两部分,它的前bit-1位是一部分,它的最后一位是一部分。一个数的二进制翻转就相当于是把它的最后一位当成首位,然后在后面接上它前bit-1为的二进制翻转。
- 而且在这个循环中我们能保证,在计算“i”的二进制翻转之前1~i-1中的所有数的二进制翻转都已经完成。“i”的前bit-1位的数值其实就是i>>1的值,直接调用i>>1的二进制翻转的结果就相当于调用了“i”的前bit-1位二进制翻转的结果。
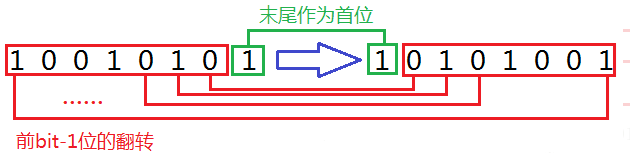
- 但是i>>1的翻转与“i”的前bit-1位的翻转是区别的!因为我们的二进制翻转始终以bit位为标准,所以i>>1会比“i”的前bit-1位多出一个前导零,而翻转之后就会多出一个“后缀零”,所以“i”的前bit-1位的翻转要去掉那个“后缀零”,也就是“rev[i>>1]>>1”。
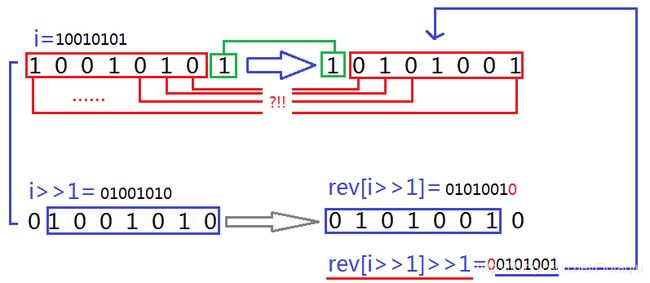
- 因此,我们只要把末尾左移 ( b i t − 1 ) (bit-1) (bit−1)位变成首位,再或上面得到的前 b i t − 1 bit-1 bit−1位翻转并处理的结果: r e v [ i > > 1 ] > > 1 rev[i>>1]>>1 rev[i>>1]>>1就是我们要的答案了。
思路来源:补充——FFT中的二进制翻转问题
int bit = 0;
while((1 << bit) < n)
bit++;
for(int i = 0; i < n; i++)
{
rev[i] = (rev[i>>1]>>1) | ((i&1)<<(bit-1));
if(i < rev[i])
swap(a[i], a[ rev[i] ]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
- 先把每个数放到最后的位置上,然后不断向上还原,同时求出点值表示。
- 可以预处理 ω n k ω^k_n ωnk和 ω n − k ω^{−k}_n ωn−k,分别存在omg和inv数组中。调用fft时,如果无需取倒数,则传入omg;如果需要取倒数,则传入inv。
cp a[N], b[N], omg[N], inv[N];
void init()
{
for(int i = 0; i < n; i++)
{
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]);
}
}
void fft(cp *a, cp *omg)
{
int lim = 0;
while((1 << lim) < n)
lim++;
for(int i = 0; i < n; i++)
{
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1)
t |= (1 << (lim - j - 1));
if(i < t)
swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
static cp buf[N];
for(int l = 2; l <= n; l *= 2)
{
int m = l / 2;
for(int j = 0; j < n; j += l)
for(int i = 0; i < m; i++)
{
buf[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m];
buf[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m];
}
for(int j = 0; j < n; j++)
a[j] = buf[j];
}
}
3、蝴蝶操作
-
“蝴蝶操作”的目的是:丢掉buf数组。
-
buf的使用:
a [ j + i ] = a [ j + i ] + o m g [ n / l ∗ i ] ∗ a [ j + i + m ] a[j + i] = a[j + i] + omg[n / l * i] * a[j + i + m] a[j+i]=a[j+i]+omg[n/l∗i]∗a[j+i+m]
a [ j + i + m ] = a [ j + i ] − o m g [ n / l ∗ i ] ∗ a [ j + i + m ] a[j + i + m] = a[j + i] - omg[n / l * i] * a[j + i + m] a[j+i+m]=a[j+i]−omg[n/l∗i]∗a[j+i+m]要求这两行不能互相影响,所以我们需要buf数组。
-
原地进行:
c p t = o m g [ n / l ∗ i ] ∗ a [ j + i + m ] cp t = omg[n / l * i] * a[j + i + m] cpt=omg[n/l∗i]∗a[j+i+m]
a [ j + i + m ] = a [ j + i ] − t a[j + i + m] = a[j + i] - t a[j+i+m]=a[j+i]−t
a [ j + i ] = a [ j + i ] + t a[j + i] = a[j + i] + t a[j+i]=a[j+i]+t
cp a[N], b[N], omg[N], inv[N];
void init(){
for(int i = 0; i < n; i++){
omg[i] = cp(cos(2 * PI * i / n), sin(2 * PI * i / n));
inv[i] = conj(omg[i]);
}
}
void fft(cp *a, cp *omg){
int lim = 0;
while((1 << lim) < n) lim++;
for(int i = 0; i < n; i++){
int t = 0;
for(int j = 0; j < lim; j++)
if((i >> j) & 1) t |= (1 << (lim - j - 1));
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
for(int l = 2; l <= n; l *= 2){
int m = l / 2;
for(cp *p = a; p != a + n; p += l)
for(int i = 0; i < m; i++){
cp t = omg[n / l * i] * p[i + m];
p[i + m] = p[i] - t;
p[i] += t;
}
}
}
高精度使用
#include 六、模板
例题:A * B Problem Plus HDU - 1402 (大数高精度乘法)
Calculate A * B.
Input
Each line will contain two integers A and B. Process to end of file.
Note: the length of each integer will not exceed 50000.
Output
For each case, output A * B in one line.
Sample Input
1
2
1000
2
Sample Output
2
2000
AC代码:
#include 七、应用-- 字符串模糊匹配
-
题意:模板串P和文本串T都带有?号,可以匹配任意一个字符,求P在T中所有的出现位置。
-
定义:文本偏移量 f ( A , B ) = s i g m a ( ∣ A [ i ] − B [ i ] ∣ ) f(A,B) = sigma(|A[i] - B[i]|) f(A,B)=sigma(∣A[i]−B[i]∣)
由于绝对值不好求,故转化为 平方
f ( A , B ) = s i g m a ( ( ∣ A [ i ] − B [ i ] ∣ ) 2 ) = s i g m a A [ i ] 2 + s i g m a B [ i ] 2 − 2 ∗ s i g m a A [ i ] ∗ B [ i ] f(A,B) = sigma((|A[i] - B[i]|)^2)= sigmaA[i] ^2+sigmaB[i] ^2-2*sigmaA[i] *B[i] f(A,B)=sigma((∣A[i]−B[i]∣)2)=sigmaA[i]2+sigmaB[i]2−2∗sigmaA[i]∗B[i] -
由于在多项式乘法中, C k ( 满 足 i + j = k ) C_k(满足i+j=k) Ck(满足i+j=k)
- 故对于字符串 A [ 0... ( N − 1 ) ] A[0...(N-1)] A[0...(N−1)]、 B [ 0... ( N − 1 ) ] B[0...(N-1)] B[0...(N−1)],我们需要将其中一个逆反,才能满足上面的算式。
- 即 b [ 0... ( N − 1 ) ] b[0...(N-1)] b[0...(N−1)] 其中 b [ i ] = [ N − i − 1 ] b[i] = [N-i-1] b[i]=[N−i−1](b是B的逆反串)
- A [ i ] A[i] A[i]与 B [ i ] B[i] B[i]比较,相当于 A [ i ] A[i] A[i]与 b [ N − i − 1 ] b[N-i-1] b[N−i−1]比较,而 i + ( N − i − 1 ) ≡ N − 1 i+(N-i-1)\equiv N-1 i+(N−i−1)≡N−1
- 因此,我们可以构造两个多项式,A,b的第i位上的字符为 x i x^i xi的系数,求 f ( A , b ) f(A, b) f(A,b),看第N位上的系数是否为0,即可判断是否匹配。
- 以上是没有通配符?的情况,显然这个复杂度O(nlogn)比kmp的O(n)要大,不划算。
-
若有通配符?,我们只需要改变一下函数 f ( A , B ) f(A,B) f(A,B)即可。
- 令? = 0,其他符号映射非零数值
- 那么只要有?不管另一个是什么,都能够匹配,即 f ( ) f() f()均等于0.
- 即 f ( A , B ) = s i g m a ( ( A [ i ] − B [ i ] ) 2 ∗ A [ i ] ∗ B [ i ] ) f(A,B)=sigma((A[i]-B[i])^2*A[i]*B[i]) f(A,B)=sigma((A[i]−B[i])2∗A[i]∗B[i])
-
若要计算 A字符串(N)、B字符串(M),在B中有多少个 B [ i , i + N ) B [i,i+N) B[i,i+N)区间,能够满足有 [ N ∗ 0.75 ] [N*0.75] [N∗0.75]的字符与A匹配(不要求连续),即有75%的字符与B子区间对应相同。
- 假设字符集 ∣ S ∣ |S| ∣S∣中为
a~b - 若 A [ i ] = = a A[i]==a A[i]==a,则令 a [ i ] = 1 a[i]=1 a[i]=1,否则 a [ i ] = 0 a[i]=0 a[i]=0, i ∈ 1... n i \in {1...n} i∈1...n
- 若 B [ i ] = = a B[i]==a B[i]==a,则令 b [ i ] = 1 b[i]=1 b[i]=1,否则 b [ i ] = 0 b[i]=0 b[i]=0, i ∈ 1... n i \in {1...n} i∈1...n
- 然后构造 f ( A , B ) = s i g m a ( a [ i ] ∗ b [ i ] ) f(A,B)=sigma(a[i]*b[i]) f(A,B)=sigma(a[i]∗b[i])
- 直接可求 a [ i ] = a [ i ] ∗ b [ i ] a[i]=a[i]*b[i] a[i]=a[i]∗b[i]
- 然后统计 c n t [ ‘ a ’ ] + = a [ i ] cnt [‘a’]+= a[i] cnt[‘a’]+=a[i],cnt[
a]即表示字符a一致的位置有多少个。 - 我们可以按照以上方法,对字符集中的每一个字符进行一遍计算,再对cnt[ ]求和,就可以得到最后匹配位置的总和。