小波变换

1多分辨率分析

都分辨率分析是一种全新而有效的信号处理与分析方法，多分辨率理论与多种分辨率下的信号（或图像）表示和分析有关。其优势很明显，某种分辨率下无法发现的特性在另一种分辨率下将很容易被发现。其作用是将信号分解成不同空间的部分。

多分辨率框架：在观察图像时，对于不同大小的物体，往往采用不同的分辨率，若物体不仅尺寸有大有小，而且对比有强有弱，则采用多分辨率进行分析则凸显出一定的优势。

分解与重构的实现：分解的最终目的是力求构造一个在频率上高度逼近的L2（R）空间的正交小波基，这些频率分辨率不同的正交小波基相当于带宽各异的带通滤波器。多分辨率分析只对低频空间做进一步分解，使频率的分辨率越来越高。

信号分解与重构matlab实现：

%信号函数定义
% 1.正弦波定义
f1=50; %频率1
f2=100; %频率2
fs=2*(f1+f2); %采样频率
Ts=1/fs; %采样间隔
N=120; %采样点数
n=1:N;
y=sin(2*pi*f1*n*Ts)+sin(2*pi*f2*n*Ts); %信号函数

% 2.小波滤波器谱分析
h=wfilters('db30','l'); %低通
g=wfilters('db30','h'); %高通

h=[h,zeros(1,N-length(h))]; %补零（圆周卷积，且增大分辨率便于观察）
g=[g,zeros(1,N-length(g))]; %补零（圆周卷积，且增大分辨率便于观察）

%3. MATLAB分解算法（圆周卷积的快速傅里叶变换实现）
sig1=ifft(fft(y).*fft(h)); %低通（低频分量）
sig2=ifft(fft(y).*fft(g)); %高通（高频分量）

%4. MATLAB重构算法
sig1=dyaddown(sig1); %2抽取
sig2=dyaddown(sig2); %2抽取

sig1=dyadup(sig1); %2插值
sig2=dyadup(sig2); %2插值

sig1=sig1(1,(1:N)); %去掉最后一个零
sig2=sig2(1,(1:N)); %去掉最后一个零

hr=h(end:-1:1); %重构低通
gr=g(end:-1:1); %重构高通

hr=circshift(hr',1)'; %位置调整圆周右移一位
gr=circshift(gr',1)'; %位置调整圆周右移一位

sig1=ifft(fft(hr).*fft(sig1)); %低频
sig2=ifft(fft(gr).*fft(sig2)); %高频

sig=sig1+sig2; %源信号

图像处理中分解与重构的实现：首先对图像先"逐行"做一维小波变换，分解为低通滤波L和高通滤波H两个分量，再“逐列”做一维小波变换，分解为LL、LH、HL、HH四个分量。L和H分别表示低通和高通滤波输出。

f=imread('7.3.1.jpg');%读入一幅图
imshow(f);%显示原图像

[c,s]=wavefast(f,1,'sym4');%利用‘sym4’小波做快速小波变换
figure;wave2gray(c,s,-6);%利用小波工具箱的函数显示变换后灰度图

[nc,y]=wavecut('a',c,s);%利用小波工具箱的函数将近似系数置0
figure;wave2gray(nc,s,-6);
edges=abs(waveback(nc,s,'sym4'));%边缘图像的重构
figure;imshow(mat2gray(edges));

利用小波分析对图像去噪

%装入图像
load tire

%下面进行噪声的产生
init=3718025452;
rand('seed',init);
Xnoise=X+18*(rand(size(X)));

%显示原始图像及它的含噪声图像
colormap(map);
subplot(2,2,1);image(wcodemat(X,192));
title('原始图像')
axis square
subplot(2,2,2);image(wcodemat(Xnoise,192));
title('含噪声的图像')
axis square

%用sym5小波对图像信号进行二层的小波分解
[c,s]=wavedec2(X,2,'sym5');

%下面进行图像的去噪声处理
%使用ddencmp函数来计算去噪的默认阈值和熵标准
%使用wdencmp函数来实现图像的压缩
[thr,sorh,keepapp]=ddencmp('den','wv',Xnoise);
[Xdenoise,cxc,lxc,perf0,perf12]=wdencmp('gbl',c,s,'sym5',2,thr,sorh,keepapp);

%显示去噪后的图像
subplot(2,2,3);image(Xdenoise);
title('去噪后的图像')
axis square

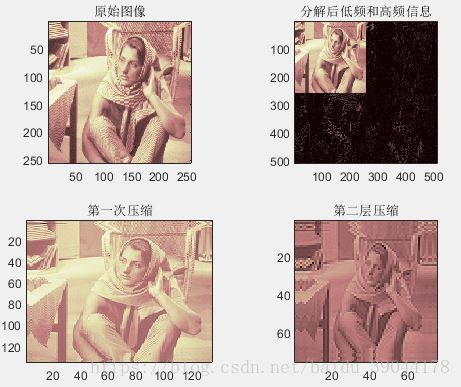
小波变换用于图像压缩：装入一幅图像，使用哈尔小波对图像进行三层分解，利用函数wdcbm()获取压缩阈值，函数wdencmp()用于对信号进行压缩。将图像分解为低频信息和高频信息，图像的主要成分包含在低频信息中，对低频信息进行两次小波分解，并改变图像的大小进行压缩，分别获取两次压缩后的图像。

%装载信号
load nelec;
indx=1:1024;
x=nelec(indx);

%用小波hear对信号进行三层分解
[c,l]=wavedec(x,3,'haar');
alpha=1.5;

%获取信号压缩的阈值
[thr,nkeep]=wdcbm(c,l,alpha);

%对信号进行压缩
[xd,cxd,lxd,perf0,perf12]=wdencmp('lvd',c,l,'haar',3,thr,'s');
subplot(2,1,1);
plot(indx,x);
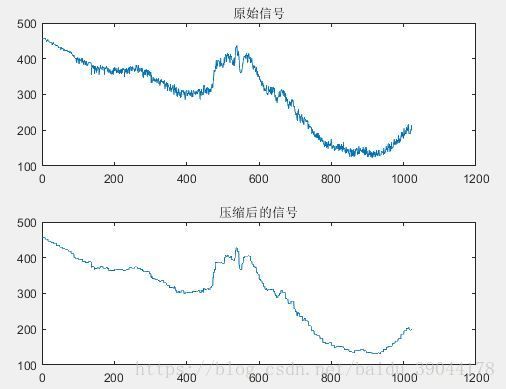
title('原始信号');
subplot(2,1,2);
plot(indx,xd);
title('压缩后的信号')

%装入图像
load tire

%下面进行噪声的产生
init=371825452;
rand('seed',init);
Xnoise=X+18*(rand(size(X)));

%显示原始图像及它的含噪声图像
colormap(map);
subplot(2,2,1);image(wcodemat(X,192));
title('原始图像')
axis square
subplot(2,2,2);image(wcodemat(Xnoise,192));
title('含噪声的图像')
axis square

%用sym5小波对图像信号进行二层小波分解
[c,s]=wavedec2(X,2,'sym5');

%下面进行图像的去噪处理
%使用ddencmp函数来计算去噪的默认阈值和熵标准
%使用wdencmp函数来实现图像的压缩
[thr,sorh,keepapp]=ddencmp('den','wv',Xnoise);
[Xdenoise,cxc,lxc,perf0,perf12]=wdencmp('gbl',c,s,'sym5',2,thr,sorh,keepapp);
%显示去噪后的图像
subplot(223),image(Xdenoise);
title('去噪后的图像')
axis square

%装入图像
load wbarb;
%显示图像
subplot(221);image(X);colormap(map)
title('原始图像');
axis square

disp('压缩前图像X的大小:');
whos('X')

%对图像用bior3.7小波进行2层小波分解
[c,s]=wavedec2(X,2,'bior3.7');

%提取小波分解结构中第一层低频系数和高频系数
ca1=appcoef2(c,s,'bior3.7',1);
ch1=detcoef2('h',c,s,1);
cv1=detcoef2('v',c,s,1);
cd1=detcoef2('d',c,s,1);

%分别对各频率成分进行重构
a1=wrcoef2('a',c,s,'bior3.7',1);
h1=wrcoef2('h',c,s,'bior3.7',1);
v1=wrcoef2('v',c,s,'bior3.7',1);
d1=wrcoef2('d',c,s,'bior3.7',1);
c1=[a1,h1;v1,d1];

%显示分解后各频率成分的信息
subplot(222);image(c1);
axis square
title('分解后低频和高频信息')

%下面进行图像压缩处理
%保留小波分解第一层低频信息；进行图像的压缩
%第一层的低频信息即为ca1，显示第一层的低频信息
%首先对第一层信息进行量化编码
ca1=appcoef2(c,s,'bior3.7',1);
ca1=wcodemat(ca1,400,'mat',0);

%改变图像的高度
ca1=0.5*ca1;
subplot(223);image(ca1);colormap(map);
title('第一次压缩');
disp('第一次压缩图像大小为:');
whos('ca1');

%保留小波分解第二层低频信息，进行图像的压缩，此时压缩比更大
%第二层的低频信息即为ca2，显示第二层的低频信息
ca2=appcoef2(c,s,'bior3.7',2);

%首先对第二层信息进行量化编码
ca2=wcodemat(ca2,440,'mat',0);
%改变图像高度
ca2=0.25*ca2;
subplot(224);image(ca2);colormap(map);
axis square
title('第二层压缩');
disp('第二层压缩的大小为:');
whos('ca2')

 

3常见小波分析

小波变换的基本思想是用一组小波函数或者基函数表示一个函数或者信号。信号分析一般是为了获得时间域与频率域的相互关系，傅里叶变换提供了有关频率域的信息，但时间方面的局部化信息却基本丢失

Haar小波：Haar函数是小波分析中最早用到的一个具有紧支撑的正交小波函数，也是最简单的小波函数，它是支撑域在0到1范围内的单个矩形波。Haar小波在时域上是不连续的，所以作为基本小波，其性能不是特别好

利用haar小波对信号进行分解并压缩信号

%装载信号
load nelec;
indx=1:1024;
x=nelec(indx);

%用小波Haar对信号进行三层分解
[c,l]=wavedec(x,3,'haar');

alpha=1.5;
%获取信号压缩的阈值
[thr,nkeep]=wdcbm(c,l,alpha);

%对信号进行压缩
[xd,cxd,lxd,perf0,perf12]=wdencmp('lvd',c,l,'haar',3,thr,'s');
subplot(2,1,1);
plot(indx,x);
title('原始信号');

subplot(2,1,2);
plot(indx,xd);
title('压缩后的信号');

利用dbl小波对图像进行分解和重构

load noiswom
[swa,swh,swv,swd]=swt2(X,3,'db1');
%使用小波dbl对noiswom图像进行三层静态小波分解
whos
%可以看出，swt2所小波分解同样不改变信号的长度，原来的96*96的图
%像做了三层分解以后，分解系数是12个96*96的图像。
colormap(map)
kp=0;
for i=1:3
subplot(3,4,kp+1),image(wcodemat(swa(:,:,i),192));
title(['Approx,cfs,level',num2str(i)])
%显示第i层近似系数图像，以192字节为单位编码
subplot(3,4,kp+2),image(wcodemat(swh(:,:,i),192));
title(['Horiz.Det.cfs level',num2str(i)])
subplot(3,4,kp+3),image(wcodemat(swv(:,:,i),192));
title(['Horiz.Det.cfs level',num2str(i)])
kp=kp+4;
end%图像分解结束

%图像重构
load noiswom
[swa,swh,swv,swd]=swt2(X,3,'db1');

%使用dbl小波对noiswom图像进行三层小波分解
mzero=zeros(size(swd));
A=mzero;
A(:,:,3)=iswt2(swa,mzero,mzero,mzero,'db1');

%使用iswt2的滤波器功能重建第三层近似系数，为了避免iswt的合成运算，注意在重建过程中，应保证其他各项系数为0.
H=mzero;V=mzero;D=mzero;
for i=1;3
swcfs=mzero;swcfs(:,:,i)=swh(:,:,i);
H(:,:,i)=iswt2(mzero,swcfs,mzero,mzero,'db1');
swcfs=mzero;swcfs(:,:,i)=swv(:,:,i);
V(:,:,i)=iswt2(mzero,mzero,swcfs,mzero,'db1');
swcfs=mzero;swcfs(:,:,i)=swh(:,:,i);
H(:,:,i)=iswt2(mzero,mzero,mzero,swcfs,'db1');
end

%分别重建1至3级的各个细节系数，同样在重建某一吸收的时候，要令其他系数为0
A(:,:,2)=A(:,:,3)+H(:,:,3)+V(:,:,3)+D(:,:,3);
A(:,:,1)=A(:,:,2)+H(:,:,2)+V(:,:,2)+D(:,:,2)

%使用递推的方法建立第一层和第二层的近似系数
colormap(map)
kp=0;
for i=1:3
subplot(3,4,kp+1),image(wcodemat(A(:,:,i),192));
title(['第',num2str(i),'层近似系数图像'],'fontsize',6)
subplot(3,4,kp+2),image(wcodemat(H(:,:,i),192));
title(['第',num2str(i),'层水平细节系数图像'],'fontsize',6)
subplot(3,4,kp+3),image(wcodemat(V(:,:,i),192));
title(['第',num2str(i),'层竖直细节系数图像'],'fontsize',6)
subplot(3,4,kp+4),image(wcodemat(D(:,:,i),192));
title(['第',num2str(i),'层对角细节系数图像'],'fontsize',6)
kp=kp+4;
end