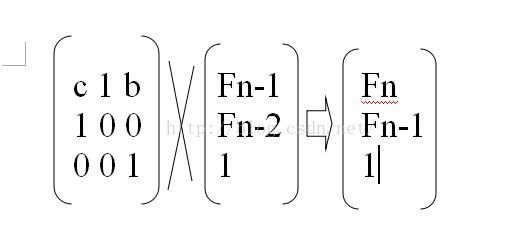hdu 5667 Sequence【矩阵快速幂】
Sequence
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 285 Accepted Submission(s): 92
Problem Description
f
Input
1≤T≤10,1≤n≤10
Output
Sample Input
1
5 3 3 3 233
Sample Output
190
1
5 3 3 3 233
Sample Output
190
题目大意:根据给出的公式,求其解fn、
思路:根据公式得出结论,求的的fn,一定是a的多少次方,所以我们锁定思路是求a的幂数。然后再用快速幂求出解。
公式不难推出:
Fn=Fn-1*c+Fn-2+b;
然后我们也不难写出矩阵:
坑点:在矩阵快速幂的时候要注意先对mod-1,再进行。也就是要注意amodp==0的情况。
然后再进行a的这些次方即可。
Ac代码:
#include
#include
#include
using namespace std;
#define ll long long int
ll mod;
typedef struct Matrix
{
ll mat[3][3];
} matrix;
matrix A,B,tmp;
Matrix matrix_mul(matrix a,matrix b)
{
matrix c;
memset(c.mat,0,sizeof(c.mat));
int i,j,k;
for(int i=0; i<3; i++)
{
for(int j=0; j<3; j++)
{
for(int k=0; k<3; k++)
{
c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
c.mat[i][j]%=mod;
}
}
}
return c;
}
Matrix matrix_quick_power(matrix a,ll k)//矩阵快速幂0.0
{
matrix b;
memset(b.mat,0,sizeof(b.mat));
for(int i=0; i<3; i++)
b.mat[i][i]=1;//单位矩阵b
while(k)
{
if(k%2==1)
{
b=matrix_mul(a,b);
k-=1;
}
else
{
a=matrix_mul(a,a);
k/=2;
}
}
return b;
}
ll Mod_pow(ll a, ll b, ll p)
{
a %= p;
ll ans = 1ll;
while (b)
{
if (b & 1)ans = ans*a%p;
a = a*a%p;
b >>= 1;
}
return ans;
}
int main()
{
ll n,a,b,c;
int t;
scanf("%d",&t);
while(t--)
{
scanf("%I64d%I64d%I64d%I64d%I64d", &n, &a, &b, &c, &mod);
A.mat[0][0] = c, A.mat[0][1] = 1, A.mat[0][2] = b;
A.mat[1][0] = 1, A.mat[1][1] = 0, A.mat[1][2] = 0;
A.mat[2][0] = 0, A.mat[2][1] = 0, A.mat[2][2] = 1;
if (n == 1)printf("1\n");
else if (n == 2)printf("%I64d\n", Mod_pow(a, b, mod));
else
{
mod--;
B = matrix_quick_power(A,(n - 2));
ll tmp=B.mat[0][0]*b+B.mat[0][2];
mod++;
ll ans = Mod_pow(a, tmp, mod);
printf("%I64d\n",ans);
}
}
}