【机器学习】神经网络详解
其他机器学习系列文章见于专题:机器学习进阶之路——学习笔记整理,欢迎大家关注。
1. 从感知机到神经网络
在上一篇博客【机器学习】感知机原理详解当中,我们介绍了感知机,这是一种二分类的线性分类模型,只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,学习能力十分有限。
将感知机扩展成为神经网络,主要从三个方面来增强表达能力:
- 隐藏层可以有多层;
- 输出层神经元可以有多个输出;
- 对激活函数作扩展,有sigmoid、tanh、softmax、ReLU等。
2. 基本结构
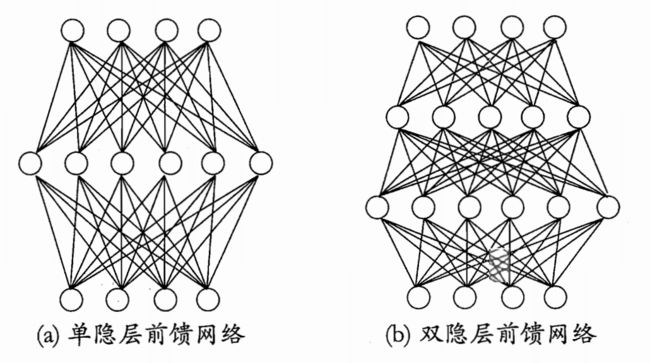
常见的神经网络结构如下图所示。其网络层可分为三类:输入层、隐藏层和输出层。
层与层之间是全互连的,不存在同层链接,也不存在跨层链接,这样的结构通常称为“多层前馈神经网络”(前馈并不意味着网络中信号不能向后传,而是指网络拓扑结构上不存在环或回路)。
3. 误差逆传播算法
误差逆传播(error BackPropagation,简称BP,又称反向传播)算法用来更新参数,它是一个迭代学习算法,基于梯度下降策略,以目标的负梯度方向对参数进行调整。
具体的更新推导过程可以参考BP推导,这里不再描述。
4. 损失函数与激活函数
4.1 均方差损失函数+Sigmoid激活函数
Sigmoid激活函数的表达式为:
σ ( z ) = 1 1 + e − z \sigma ( z ) = \frac { 1 } { 1 + e ^ { - z } } σ(z)=1+e−z1
函数图像如下:
当 z z z绝对值越来越大,函数曲线趋于平缓, σ ′ ( z ) \sigma ^ { \prime } ( z ) σ′(z)越来越小。通常反向传播算法使用均方差作为损失函数,每一层向前递推都要乘以 σ ′ ( z ) \sigma ^ { \prime } ( z ) σ′(z)得到梯度变化值。这意味着在大多数时候,我们的梯度变化值很小,导致我们的W,b更新到极值的速度较慢,也就是我们的算法收敛速度较慢。
4.2 使用交叉熵损失函数+Sigmoid激活函数改进DNN算法收敛速度
为了解决sigmoid激活函数和均方差损失函数导致的收敛速度慢的问题,一种解决方法时替换掉sigmoid,另一种方法是利用交叉熵损失函数来代替均方差损失函数。
二分类时每个样本的交叉熵损失函数的形式为:
J ( W , b , a , y ) = − [ y ln a + ( 1 − y ) ln ( 1 − a ) ] J ( W , b , a , y ) = - [ y \ln a + ( 1 - y ) \ln ( 1 - a ) ] J(W,b,a,y)=−[ylna+(1−y)ln(1−a)]
使用交叉熵,得到的的 δ l \delta ^ { l } δl梯度表达式中没有了 σ ′ ( z ) \sigma ^ { \prime } ( z ) σ′(z),这样W和b的更新公式中也不包含 σ ′ ( z ) \sigma ^ { \prime } ( z ) σ′(z),因此避免了反向传播收敛速度慢的问题。
4.3 使用对数似然损失函数和softmax激活函数进行DNN分类输出
如果是分类问题,那么输出是一个个的类别,比如有三个类别,对应输出层有三个神经元。此时DNN分类模型要求是输出层神经元输出的值在0到1之间,同时所有输出值之和为1。
我们可以将输出层第 i i i个神经元的激活函数定义为如下形式:
a i L = e z i L ∑ j = 1 n L e z j L a _ { i } ^ { L } = \frac { e ^ { z _ { i } ^ { L } } } { \sum _ { j = 1 } ^ { n _ { L } } e ^ { z _ { j } ^ { L } } } aiL=∑j=1nLezjLeziL
其中, n L n_L nL是输出层第 L L L层的神经元个数,或者说我们的分类问题的类别数。 ∑ j = 1 n L e z j L \sum _ { j = 1 } ^ { n _ { L } } e ^ { z _ { j } ^ { L } } ∑j=1nLezjL作为归一化因子保证了所有的 a i L a _ { i } ^ { L } aiL之和为1。
4.4 梯度爆炸梯度消失与ReLU激活函数
在DNN中,有一个梯度消失和爆炸的问题。什么是梯度爆炸和梯度消失呢?就是在反向传播的算法过程中,由于我们使用了是矩阵求导的链式法则,有一大串连乘,如果连乘的数字在每层都是小于1的,则梯度越往前乘越小,导致梯度消失,而如果连乘的数字在每层都是大于1的,则梯度越往前乘越大,导致梯度爆炸。
对于梯度爆炸,则一般可以通过调整我们DNN模型中的初始化参数得以解决。
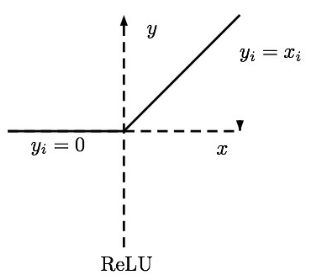
梯度消失问题无法完美解决,一个可能部分解决梯度消失问题的办法是使用ReLU(Rectified Linear Unit,修正线性单元)激活函数,ReLU在卷积神经网络CNN中得到了广泛的应用,在CNN中梯度消失似乎不再是问题。CNN表达式为:
σ ( z ) = max ( 0 , z ) \sigma ( z ) = \max ( 0 , z ) σ(z)=max(0,z)
4.5 其他激活函数
(1) tanh:是sigmoid的变种,表达式为:
tanh ( z ) = e z − e − z e z + e − z \tanh ( z ) = \frac { e ^ { z } - e ^ { - z } } { e ^ { z } + e ^ { - z } } tanh(z)=ez+e−zez−e−z
tanh激活函数和sigmoid激活函数的关系为:
tanh ( z ) = 2 sigmoid ( 2 z ) − 1 \tanh ( z ) = 2 \operatorname { sigmoid } ( 2 z ) - 1 tanh(z)=2sigmoid(2z)−1
(2) softplus:这个其实就是sigmoid函数的原函数,表达式为:
s o f t p l u s ( z ) = log ( 1 + e z ) softplus( z ) = \log \left( 1 + e ^ { z } \right) softplus(z)=log(1+ez)
它的导数就是sigmoid函数。
5. 正则化
神经网络的正则化方法包括L1&L2正则化、集成学习的思路正则化、dropout正则化、增强数据集正则化等,具体可参考深度神经网络(DNN)的正则化。
参考文献:
- BP推导——续
- 深度神经网络(DNN)模型与前向传播算法
- 深度神经网络(DNN)损失函数和激活函数的选择
- 深度神经网络(DNN)的正则化