计蒜客 2020 蓝桥杯大学 B 组省赛模拟赛（一）

题目传送门

建立了自己的个人博客，朝着秃头的路上一去不返。。。
作者是个打铁弱鸡，若各位大佬发现了错误请在评论指出。

A. 结果填空：有趣的数字

蓝桥杯标准的送温暖题，枚举每个数判断是否含有数字5并进行判素数后计数即可。

const int MAXN = 100000;

bool check(int n) {
    while(n) {
        if(n % 10 == 5) return true;
        n /= 10;
    }
    return false;
}
bool prime(int n) {
    if(n < 2) return false;
    bool ret = true;
    for(int i = 2; i * i <= n; i++) {
        if(n % i == 0) ret = false;
    }
    return ret;
}
int main() {
    int cnt = 0;
    for(int i = 1; i <= MAXN; i++)
        if(check(i) && prime(i)) cnt++;
    cout << cnt << endl;
    return 0;
}

B. 结果填空：爬楼梯

超级经典的dp，蓝桥杯日常经典题变形。
萌新可以先做牛客的这道题 传送门

• 通过暴力枚举我们可以发现当步数为1和2时，方案数为1 1 2 3 5 8 11，为斐波那契数列。但显然，暴力是没有前途的，下面介绍另一种方法。
• 定义$F(i)$为走到第$i$级台阶的方案数，则显然可得当 $i>2$ 时有$F(i)=F(i-1)+F(i-2)$。因为要走到第$i$级台阶，可以是由$i-1$级台阶上来也可以是由$i-2$级台阶上来，所以第$i$级的方案数应等于两者之和。
• 此题是一次最多可以上四级台阶，但第5级和第7级不能踩，则可以得到表达式$F(i)=F(i-1)+F(i-2)+F(i-3)+F(i-4)$，并特判$F(5)=F(7)=0$。
• 到这里就可以写出简单的递归程序了，但是只会写递归是没有前途的(手动滑稽)，所以给出非递归的dp版，当然下面的版本完全可以预处理前四项来精简代码。

int a[117];
int main() {
    a[0] = 1;
    for(int i = 1; i <= 10; i++) {
        if(i == 5 || i == 7) continue;
        if(i - 1 >= 0) a[i] += a[i - 1];
        if(i - 2 >= 0) a[i] += a[i - 2];
        if(i - 3 >= 0) a[i] += a[i - 3];
        if(i - 4 >= 0) a[i] += a[i - 4];
    }
    for(int i = 1; i <= 10; i++) cout << a[i] << endl;
    return 0;
}

C. 结果填空：七巧板

和用直线划分平面的原理是一样的，每次新增的区域数是一个以1为首项公差为1的等差数列。
跳进了唯一的坑里：请在下图的基础上，图中一开始就有7个区域。

int ans, det;
int main() {
    ans = 7, det = 6;
    for(int i = 0; i < 5; i++) ans += det++;
    cout << ans << endl;
    return 0;
}

D. 结果填空：苹果

在网上看到的大多是贪心的写法，大致上都是在当前能选3就选3，不能选再和旁边的并用，但都存在反例。做的时候也考虑过贪心但未能成功证明，于是写了个暴力的递归来枚举所有的情况，稍微剪枝优化后时间在1s左右。此题个人认为此题应该是dp，但学艺不精没写出dp来。。。

int ans = 0;
int a[117] = {7, 2, 12, 5, 9, 9, 8, 10, 7, 10, 5, 4, 5, 8, 4, 4, 10, 11, 3, 8, 7, 8, 3, 2, 1, 6, 3, 9, 7, 1};
int sum[117];
void dfs(int idex, int num) {
    if(idex == 30) {
        ans = max(ans, num);
        return;
    }
    if(sum[idex] / 3 + num < ans) return;//剪枝优化
    //不共用
    dfs(idex + 1, num + a[idex] / 3);
    //往后共用
    if(idex + 2 < 30) {
        int min_num = min(a[idex], a[idex + 1]);
        min_num = min(min_num, a[idex + 2]);//共用最多能分几个
        for(int k = 1; k <= min_num; k++) {
            for(int i = 0; i < 3; i++) a[idex + i] -= k;
            dfs(idex + 1, num + a[idex] / 3 + k);
            for(int i = 0; i < 3; i++) a[idex + i] += k;
        }
    }
}
int main() {
    for(int i = 29; i >= 0; i--) sum[i] = sum[i + 1] + a[i];
    dfs(0, 0);
    cout << ans << endl;
    return 0;
}

正确的姿势dp：从这位大佬这里学到了dp的解法，快去看看大佬的博客。

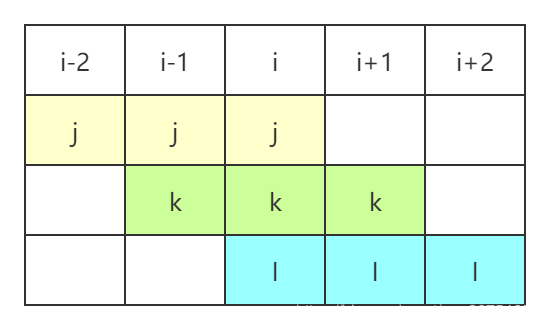
• 其实这个dp并不难，主要是没想清楚，画图能有效的帮助理解。
• 如上图所示，对于第$i$个篮子里的苹果凑齐三个一共有四种方式：往左共用、中间共用、往右共用和本身自己凑齐三个。
• 可以定义$dp[i][j][k][l]$表示前$i$个篮子的答案，则有状态转移方程$dp[i][j][k][l]=max(dp[i-1][m][j][k]+(a[i]-j-k-l)/3+j)$。
• 上式应满足$i+j+k\le a[i]$，且$i,j,k\in [0,2]$。
• 可进一步优化成$dp[i][j][k]$省略第一种状态，详见代码。

int a[37] = {0, 7, 2, 12, 5, 9, 9, 8, 10, 7, 10, 5, 4, 5, 8, 4, 4, 10, 11, 3, 8, 7, 8, 3, 2, 1, 6, 3, 9, 7, 1};
int ans, dp[37][7][7];
int main() {
    ans = 0;
    memset(dp, negative_infinite, sizeof(dp));
    dp[0][0][0] = 0;
    for(int i = 1; i <= 30; i++) {
        for(int j = 0; j < 3; j++) {
            for(int k = 0; k < 3; k++) {
                for(int l = 0; l < 3; l++) {
                    if(j + k + l <= a[i]) {
                        dp[i][k][l] = max(dp[i][k][l], dp[i - 1][j][k] + (a[i] - j - k - l) / 3 + j);
                        ans = max(ans, dp[i][k][l]);
                    }
                }
            }
        }
    }
    cout << ans << endl;
    return 0;
}

E. 结果填空：方阵

• 设点A坐标为$(x1，y1)$，点B坐标为$(x2，y2)$，当且仅当$gcd(x1-x2，y1-y2)=1$时AB连线上没有其它点。因为若不互质，则存在相似三角形可以找到其它点。
• 解法一：枚举所有可能的点对，判断x轴距离和y轴距离是否互斥，复杂度$o(n^4)$。
• 解法二：枚举所有可能的x轴距离和y轴距离，算出对答案的贡献求和，但要注意特判某一边为0的情况。

LL n = 1000, k = 500 * 500, ans = 0;
int main() {
    for(int i = 1; i < n; i++)
        for(int j = 1; j < n; j++)
            if(__gcd(i, j) == 1 && i * i + j * j <= k)
                ans = (ans + 2 * (n - i) * (n - j) % mod) % mod;
    ans = (ans + 2 * n * (n - 1) % mod) % mod;
    cout << ans << endl;
    return 0;
}

F. 程序设计：寻找重复项

题意简单明了，作为c++选手，直接使用了STL库。

• 解法一：Hash
• 解法二：维护一个有序序列，二分进行查找和插入，复杂度logn
• 对于萌新：各种库函数和板子当然可用，但不能依赖，不然岂不本末倒置。

const int MAXN = 2e6;

LL a, b, c;
LL num[MAXN + 117];
unordered_set<int> s;
int main() {
    num[0] = 1;
    s.insert(1);
    scanf("%lld%lld%lld", &a, &b, &c);
    for(int i = 1; i <= MAXN; i++) {
        num[i] = (a * num[i - 1] + num[i - 1] % b) % c;
        if(s.count(num[i])) {
            printf("%d\n", i);
            break;
        } else s.insert(num[i]);
        if(i == MAXN)  puts("-1");
    }
    return 0;
}

G. 程序设计：被袭击的村庄

• 题意是个坑点：现在，给定上述的所有信息，我们想知道A村被袭击之后的道路、房屋、田地的总伤害，以及全村的总伤害。 正确的应该是输出被袭击之后道路、房屋、田地耐久度为0的数量和全村的总伤害。
• 模拟题，维护一个decrement矩阵来记录耐久度的减少量。
• 对于每一发炮弹，更新对应伤害范围内的耐久度，对于高级炮弹还需特判溅射伤害。

const int MAXN = 300 + 117;

int n, m, k;
LL a, b, c, w;
LL harm[MAXN][MAXN];//炮弹的范围伤害
LL decrement[MAXN][MAXN];//耐久度的减少量
int village[MAXN][MAXN];//村庄布局
int q, id, x, y;
LL road, house, field, sum;
int dx[8] = { -1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = { -1, 0, 1, -1, 1, -1, 0, 1};
bool check(int x, int y) {//判断坐标是否合法
    if(x < 0 || x >= n) return false;
    if(y < 0 || y >= m) return false;
    return true;
}
void sputtering(int x, int y) {//往周围8个格子溅射伤害
    for(int i = 0; i < 8; i++) {
        if(check(x + dx[i], y + dy[i]))
            decrement[x + dx[i]][y + dy[i]] += w;
    }
}
void solve() {
    int bex = x - k / 2, bey = y - k / 2;
    for(int i = 0; i < k; i++) {
        for(int j = 0; j < k; j++) {
            if(check(bex + i, bey + j)) {
                decrement[bex + i][bey + j] += harm[i][j];
                if(id == 0) sputtering(bex + i, bey + j);
            }
        }
    }
}
void pr() {
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < m; j++) {
            if(village[i][j] == 1) {
                //road += min(decrement[i][j], a);
                road += decrement[i][j] >= a;
                sum += min(decrement[i][j], a);
            } else if(village[i][j] == 2) {
                //house += min(decrement[i][j], b);
                house += decrement[i][j] >= b;
                sum += min(decrement[i][j], b);
            } else {
                //field += min(decrement[i][j], c);
                field += decrement[i][j] >= c;
                sum += min(decrement[i][j], c);
            }
        }
    }
    cout << road << " " << house << " " << field << endl;
    cout << sum << endl;
}
int main() {
    cin >> n >> m;
    cin >> a >> b >> c;
    cin >> k >> w;
    for(int i = 0; i < k; i++)
        for(int j = 0; j < k; j++)
            cin >> harm[i][j];
    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
            cin >> village[i][j];
    cin >> q;
    while(q--) {
        cin >> id >> x >> y;
        x--, y--;
        solve();
    }
    pr();
    return 0;
}

H. 程序设计：字符串

• 此题需要前置技能点：模运算，即89%M = (8*10%M + 9*1%M)%M。
• 先假设进制为10进制，题意为给定一个数，至多交换两位数字使得到的数字是M的倍数。
  题目中说到多解输出字典序最小，则容易想到枚举。考虑一下复杂度，枚举交换的位置需要o($n^2$)，计算mod需要o($n^1$)，总的复杂度o($n^3$)。
• 对多次取模操作进行优化，假设$a=123\%M,b=321\%M$，考虑123和321之间的关系：$321=123-1\ast 100-3\ast 1+3\ast 100+1\ast 1$，根据模运算则有$b=(a-1\ast 100-3\ast 1+3\ast 100+1\ast 1)\%M$。即假设交换任意$i$位置和$j$位置的数，A为交换前的值，B为交换后的值，有$B=(A-i\ast 10^i-j\ast 10^j+i\ast 10^j+j\ast 10^i)\%M$，复杂度O(1)。
• 最后，进制为26，需要预处理一下幂次的取模，以及注意减法运算时答案的取正。

const int MAXN = 2000 + 117;

char s[MAXN];
int len;
int a[MAXN];
int fact[MAXN];
int M;
int num, now;
void sub(int mul, int order) {//now=now-mul*26^order
    int sum = fact[order];
    sum = sum * mul % M;
    now = ((now - sum) % M + M) % M;
}
void add(int mul, int order) {//now=now+mul*26^order
    int sum = fact[order];
    sum = sum * mul % M;
    now = (now + sum) % M;
}
void init() {//预处理幂次
    scanf("%s", s);
    scanf("%d", &M);
    fact[0] = 1;
    for(int i = 1; i < MAXN; i++) fact[i] = fact[i - 1] * 26 % M;
    len = strlen(s);
    for(int i = 0; i < len; i++) {
        a[i] = s[i] - 'A';
        num = (num * 26 + a[i]) % M;
    }
}
int main() {
    init();
    if(num == 0) puts("0 0");
    else {
        bool pr = false;
        for(int i = 0; i < len && !pr; i++) {
            for(int j = 0; j < len && !pr; j++) {
                now = num;
                sub(a[i], len - 1 - i);
                sub(a[j], len - 1 - j);
                add(a[i], len - 1 - j);
                add(a[j], len - 1 - i);
                if(now == 0) {
                    printf("%d %d\n", i + 1, j + 1);
                    pr = true;
                }
            }
        }
        if(!pr) puts("-1 -1");
    }
    return 0;
}

I. 程序设计：最短路

• 此题需要前置技能点：单源最短路Dij的堆优化,如果你会了Dij的堆优化，那么就可以做此题了。
• 题目要求从起点到每个点再回来的最短路径的总和。对于一个点，有：来回最短路 = 去最短路 + 回最短路
• 利用Dij可求得起点去每个点的最短路，回的最短路容易想到对每个点都用一遍Dij，但这种做法的复杂度$o(n^3)$。可以注意到，无论怎么样起点总是固定的，如若将所有的边都反向，则跑一遍Dij即可求得所有回来的最短路，如下图。
  

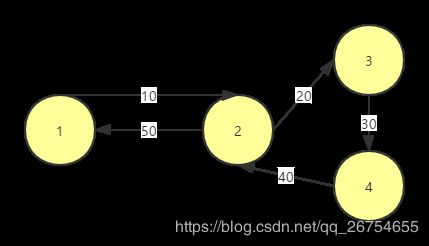
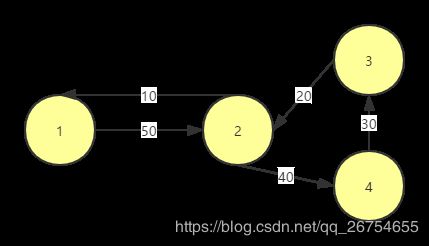
const int MAXN = 6e4 + 117;

int t;
struct qnode {
    int v;
    LL c;
    qnode(int _v = 0, LL _c = 0): v(_v), c(_c) {}
    bool operator <(const qnode &r)const {
        return c > r.c;
    }
};
struct Edge {
    int v;
    LL cost;
    Edge(int _v = 0, LL _cost = 0): v(_v), cost(_cost) {}
};
vector<Edge> E[2][MAXM];
bool vis[MAXN];
LL dist[2][MAXN];
void Dijstra(int flag, int n, int start) {
    memset(vis, false, sizeof(vis));
    for(int i = 1; i <= n; i++) dist[flag][i] = 1e18;
    priority_queue<qnode> que;
    while(!que.empty()) que.pop();
    dist[flag][start] = 0;
    que.push(qnode(start, 0));
    qnode tmp;
    while(!que.empty()) {
        tmp = que.top();
        que.pop();
        int u = tmp.v;
        if(vis[u]) continue;
        vis[u] = true;
        for(int i = 0; i < E[flag][u].size(); i++) {
            int v = E[flag][tmp.v][i].v;
            int cost = E[flag][u][i].cost;
            if(!vis[v] && dist[flag][v] > dist[flag][u] + cost) {
                dist[flag][v] = dist[flag][u] + cost;
                que.push(qnode(v, dist[flag][v]));
            }
        }
    }
}
void addedge(int flag, int u, int v, LL w) {
    E[flag][u].push_back(Edge(v, w));
}
int n, m;
LL sum;
void init() {
    sum = 0;
    for(int i = 0; i < MAXM; i++) {
        E[0][i].clear();
        E[1][i].clear();
    }
}
int main() {
    scanf("%d", &t);
    while(t--) {
        init();
        scanf("%d%d", &n, &m);
        int u, v;
        LL w;
        while(m--) {
            scanf("%d %d %lld", &u, &v, &w);
            addedge(0, u, v, w);
            addedge(1, v, u, w);
        }
        Dijstra(0, n, 1);
        Dijstra(1, n, 1);
        for(int i = 1; i <= n; i++) sum += dist[0][i] + dist[1][i];
        printf("%lld\n", sum);
    }
    return 0;
}

J. 程序设计：迷宫

• 广搜模板题，注意以下细节即可。
• 传送门尽头是障碍物不能移动
• 传送门尽头是终点
• 传送门尽头是传送门构成链或者环

const int MAXN = 1000 + 117;

int n, m, q;
int enx, eny; //终点
int dx[4] = { -1, 0, 0, 1};
int dy[4] = {0, -1, 1, 0};
char s[MAXN][MAXN];//地图
bool gameover, f[MAXN][MAXN]; //访问标记
struct node { //传送门
    int a, b;
    int c, d;
} csm[117];
struct point { //点
    int x, y;
    int step;
} now, ne;
bool check_point(point p) {//点是否合法
    if(p.x <= 0 || p.x > n) return false;
    if(p.y <= 0 || p.y > m) return false;
    if(s[p.x][p.y] == '*') return false;
    if(f[p.x][p.y]) return false;
    f[p.x][p.y] = true;
    return true;
}
int check_node(point p) {//判断是否是传送门
    for(int i = 0; i < q; i++)
        if(p.x == csm[i].a && p.y == csm[i].b) return i;
    return -1;
}
point to_node(point p, int id) {//到达传送门的尽头
    p.x = csm[id].c;
    p.y = csm[id].d;
    if(p.x == enx && p.y == eny) {
        gameover = true;
        return p;
    }
    if(!check_point(p)) {
        p.x = p.y = -1;
        return p;
    } else {
        int node_id = check_node(p);
        if(node_id != -1) return to_node(p, node_id);
        return p;
    }
}
void BFS() {//广搜迷宫
    gameover = false;
    memset(f, false, sizeof(f));
    queue<point> q;
    q.push({1, 1, 0});
    f[1][1] = true;
    while(!q.empty()) {
        now = q.front();
        q.pop();
        int node_id = check_node(now);
        if(node_id != -1) now = to_node(now, node_id);
        if(now.x == enx && now.y == eny) gameover = true;
        if(gameover) {
            printf("%d\n", now.step);
            break;
        }
        for(int i = 0; i < 4; i++) {
            ne.x = now.x + dx[i];
            ne.y = now.y + dy[i];
            ne.step = now.step + 1;
            if(check_point(ne)) q.push(ne);
        }
    }
    if(!gameover) puts("No solution");
}
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%s", s[i] + 1);
    scanf("%d", &q);
    for(int i = 0; i < q; i++)
        scanf("%d%d%d%d", &csm[i].a, &csm[i].b, &csm[i].c, &csm[i].d);
    scanf("%d%d", &enx, &eny);
    BFS();
    return 0;
}