离散数学【关系】习题解析 序偶,直积,关系图,关系矩阵,哈斯图
下面是习题与解析
文章目录
- 第一题 序偶与类型
- 第二题 关系图,矩阵与类型
- 第三题关系图,矩阵与类型
- 第四题 复合关系
- 第五题 求t( R)
- 第六题 求表达式
- 第七题 求关系图等价类
- 第八题 写出序偶与哈斯图
第一题 序偶与类型
(1) 解:
R={<1,2>,<1,4>,<1,6>,<2,1>,<2,2>,<2,4>,<2,6>,<4,1>,<4,2>,<4,4>,<4,6>,<6,1>,<6,2>,<6,4>,<6,6>}
因为 1+1=2
所以<1,1> ∉ \notin ∈/ R ,<2,2> ∉ \notin ∈/R R既不是自反,也不是反自反
关系矩阵如下
R = [ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] R=\begin{bmatrix} 0&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1 \end{bmatrix} R=⎣⎢⎢⎡0111111111111111⎦⎥⎥⎤
可以看出,R为对称矩阵,是对称的
M R ∘ R = [ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] ∘ [ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] = [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] M R\circ R=\begin{bmatrix} 0&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1 \end{bmatrix} \circ \begin{bmatrix} 0&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1 \end{bmatrix} =\begin{bmatrix} 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1 \end{bmatrix} MR∘R=⎣⎢⎢⎡0111111111111111⎦⎥⎥⎤∘⎣⎢⎢⎡0111111111111111⎦⎥⎥⎤=⎣⎢⎢⎡1111111111111111⎦⎥⎥⎤
因为 M R ∘ \circ ∘R ≥ \geq ≥MR,所以MR不是可传递的
(2) R={<1,2>,<1,4>,<1,6>,<2,4>,<2,6>,<4,6>}
因为 <1,1>,<2,2>,<4,4>,<6,6> ∉ \notin ∈/ R,所以是反自反的
关系矩阵
R = [ 0 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] R=\begin{bmatrix} 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} R=⎣⎢⎢⎡0000100011001110⎦⎥⎥⎤
显然是不对称的
M R ∘ R = [ 0 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] ∘ [ 0 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] = [ 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 ] MR\circ R=\begin{bmatrix} 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} \circ \begin{bmatrix} 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} =\begin{bmatrix} 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} MR∘R=⎣⎢⎢⎡0000100011001110⎦⎥⎥⎤∘⎣⎢⎢⎡0000100011001110⎦⎥⎥⎤=⎣⎢⎢⎡0000000010001100⎦⎥⎥⎤
因为M R ∘ \circ ∘ R ≤ \leq ≤MR,所以是可传递的
第二题 关系图,矩阵与类型
R的关系矩阵
R = [ 1 0 0 1 0 0 0 0 1 1 0 1 0 0 1 0 ] R=\begin{bmatrix} 1&0&0&1\\ 0&0&0&0\\ 1&1&0&1\\ 0&0&1&0 \end{bmatrix} R=⎣⎢⎢⎡1010001000011010⎦⎥⎥⎤
R的关系图
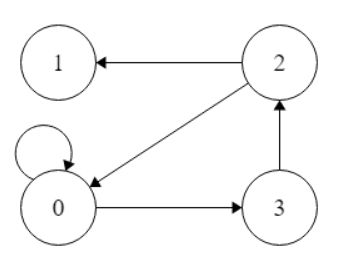
如图,1,2,3节点没有自旋,0有自旋,所以既不是自反,也不是反自反
从关系矩阵中,<2,3><3,2>对称,所以可以看出既不是对称,也不是反对称
M R ∘ R = [ 1 0 0 1 0 0 0 0 1 1 0 1 0 0 1 0 ] ∘ [ 1 0 0 1 0 0 0 0 1 1 0 1 0 0 1 0 ] = [ 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 ] MR\circ R=\begin{bmatrix} 1&0&0&1\\ 0&0&0&0\\ 1&1&0&1\\ 0&0&1&0 \end{bmatrix} \circ \begin{bmatrix} 1&0&0&1\\ 0&0&0&0\\ 1&1&0&1\\ 0&0&1&0 \end{bmatrix} =\begin{bmatrix} 1&0&1&1\\ 0&0&0&0\\ 1&0&1&1\\ 1&1&0&1 \end{bmatrix} MR∘R=⎣⎢⎢⎡1010001000011010⎦⎥⎥⎤∘⎣⎢⎢⎡1010001000011010⎦⎥⎥⎤=⎣⎢⎢⎡1011000110101011⎦⎥⎥⎤
所以M R ∘ \circ ∘ R ≰ \nleq ≰MR,所以不是可传递的
第三题关系图,矩阵与类型
R的关系图
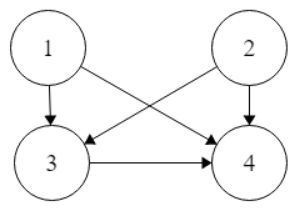
R的关系矩阵
R = [ 0 0 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] R=\begin{bmatrix} 0&0&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} R=⎣⎢⎢⎡0000000011001110⎦⎥⎥⎤
从关系图可知
-
顶点没有自旋,所以是反自反的
-
任意点之间只有单向的边,所以是反对称的
从关系矩阵计算
M R ∘ R = [ 0 0 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] ∘ [ 0 0 1 1 0 0 1 1 0 0 0 1 0 0 0 0 ] = [ 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 ] MR \circ R=\begin{bmatrix} 0&0&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} \circ \begin{bmatrix} 0&0&1&1\\ 0&0&1&1\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} =\begin{bmatrix} 0&0&0&1\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} MR∘R=⎣⎢⎢⎡0000000011001110⎦⎥⎥⎤∘⎣⎢⎢⎡0000000011001110⎦⎥⎥⎤=⎣⎢⎢⎡0000000000001100⎦⎥⎥⎤
因为M R ∘ \circ ∘ R ≤ \leq ≤MR
所以是可传递的
第四题 复合关系
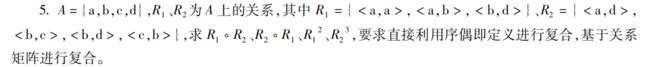
R1,R2的关系矩阵
R 1 = [ 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] R 2 = [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] R_1=\begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} R_2=\begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} R1=⎣⎢⎢⎡1000100000000100⎦⎥⎥⎤R2=⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤
R 1 ∘ R 2 = [ 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] ∘ [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] = [ 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 ] R_1\circ R_2=\begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} \circ \begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} =\begin{bmatrix} 0&0&1&1\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} R1∘R2=⎣⎢⎢⎡1000100000000100⎦⎥⎥⎤∘⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤=⎣⎢⎢⎡0000000010001000⎦⎥⎥⎤
R 2 ∘ R 1 = [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] ∘ [ 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] = [ 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 ] R_2\circ R_1= \begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} \circ \begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix}= \begin{bmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&1\\ 0&0&0&0 \end{bmatrix} R2∘R1=⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤∘⎣⎢⎢⎡1000100000000100⎦⎥⎥⎤=⎣⎢⎢⎡0000000000000010⎦⎥⎥⎤
R 1 2 = [ 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] ∗ [ 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 ] = [ 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 ] R_1^2= \begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} * \begin{bmatrix} 1&1&0&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} =\begin{bmatrix} 1&1&0&1\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix} R12=⎣⎢⎢⎡1000100000000100⎦⎥⎥⎤∗⎣⎢⎢⎡1000100000000100⎦⎥⎥⎤=⎣⎢⎢⎡1000100000001000⎦⎥⎥⎤
R 2 3 = [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] ∗ [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] ∗ [ 0 0 0 1 0 0 1 1 0 1 0 0 0 0 0 0 ] = [ 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 ] R_2^3= \begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} * \begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} * \begin{bmatrix} 0&0&0&1\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} =\begin{bmatrix} 0&0&0&0\\ 0&0&1&1\\ 0&1&0&0\\ 0&0&0&0 \end{bmatrix} R23=⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤∗⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤∗⎣⎢⎢⎡0000001001001100⎦⎥⎥⎤=⎣⎢⎢⎡0000001001000100⎦⎥⎥⎤
第五题 求t( R)
R={
R的关系矩阵
M = [ 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 ] M=\begin{bmatrix} 0&1&0&0&0\\ 0&0&1&0&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix} M=⎣⎢⎢⎢⎢⎡0000010000010100010001001⎦⎥⎥⎥⎥⎤
自反闭包r(R ),将主对角线补齐即可
M r ( R ) = [ 1 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 ] M~r(R)~=\begin{bmatrix} 1&1&0&0&0\\ 0&1&1&0&1\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{bmatrix} M r(R) =⎣⎢⎢⎢⎢⎡1000011000011100011001001⎦⎥⎥⎥⎥⎤
对称闭包s(R ),将不成对的1补全
M s ( R ) = [ 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 ] M~s(R)~=\begin{bmatrix} 0&1&0&0&0\\ 1&0&1&0&1\\ 0&1&0&1&0\\ 0&0&1&0&0\\ 0&1&0&0&1 \end{bmatrix} M s(R) =⎣⎢⎢⎢⎢⎡0100010101010100010001001⎦⎥⎥⎥⎥⎤
WarShall求t(R),从i列计算,j行有为1的,将第i行加到j行
M = [ 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 ] M 12 = [ 0 1 1 0 1 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 ] M=\begin{bmatrix} 0&1&0&0&0\\ 0&0&1&0&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix} M12=\begin{bmatrix} 0&1&1&0&1\\ 0&0&1&0&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix} M=⎣⎢⎢⎢⎢⎡0000010000010100010001001⎦⎥⎥⎥⎥⎤M12=⎣⎢⎢⎢⎢⎡0000010000110100010011001⎦⎥⎥⎥⎥⎤
M 13 = [ 0 1 1 1 1 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 ] M 23 = [ 0 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 ] M 43 = [ 0 1 1 1 1 0 0 1 1 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 ] M13=\begin{bmatrix} 0&1&1&1&1\\ 0&0&1&0&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix} M23=\begin{bmatrix} 0&1&1&1&1\\ 0&0&1&1&1\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix} M43=\begin{bmatrix} 0&1&1&1&1\\ 0&0&1&1&1\\ 0&0&0&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{bmatrix} M13=⎣⎢⎢⎢⎢⎡0000010000110101010011001⎦⎥⎥⎥⎥⎤M23=⎣⎢⎢⎢⎢⎡0000010000110101110011001⎦⎥⎥⎥⎥⎤M43=⎣⎢⎢⎢⎢⎡0000010000110101111011001⎦⎥⎥⎥⎥⎤
M 14 = [ 0 1 1 1 1 0 0 1 1 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 ] M 15 = [ 0 1 1 1 1 0 0 1 1 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 ] M14=\begin{bmatrix} 0&1&1&1&1\\ 0&0&1&1&1\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{bmatrix} M15=\begin{bmatrix} 0&1&1&1&1\\ 0&0&1&1&1\\ 0&0&1&1&0\\ 0&0&1&1&0\\ 0&0&0&0&1 \end{bmatrix} M14=⎣⎢⎢⎢⎢⎡0000010000111101111011001⎦⎥⎥⎥⎥⎤M15=⎣⎢⎢⎢⎢⎡0000010000111101111011001⎦⎥⎥⎥⎥⎤
最后的M15就是传递闭包
第六题 求表达式

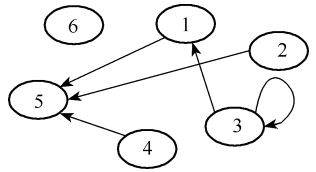
R的关系矩阵
M = [ 0 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 ] M R 2 = [ 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] M R 3 = [ 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] M=\begin{bmatrix} 0&0&0&0&1&0\\ 0&0&0&0&1&0\\ 1&0&1&0&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{bmatrix} MR^2=\begin{bmatrix} 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 1&0&1&0&1&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{bmatrix} MR^3=\begin{bmatrix} 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 1&0&1&0&1&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{bmatrix} M=⎣⎢⎢⎢⎢⎢⎢⎡001000000000001000000000110100000000⎦⎥⎥⎥⎥⎥⎥⎤MR2=⎣⎢⎢⎢⎢⎢⎢⎡001000000000001000000000001000000000⎦⎥⎥⎥⎥⎥⎥⎤MR3=⎣⎢⎢⎢⎢⎢⎢⎡001000000000001000000000001000000000⎦⎥⎥⎥⎥⎥⎥⎤
t ( R ) = [ 1 0 0 0 1 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 1 ] s ( R ) = [ 0 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 0 0 0 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 0 0 ] r ( R ) = [ 0 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 ] t(R)=\begin{bmatrix} 1&0&0&0&1&0\\ 0&1&0&0&1&0\\ 1&0&1&0&0&0\\ 0&0&0&1&1&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{bmatrix} s(R)=\begin{bmatrix} 0&0&1&0&1&0\\ 0&0&0&1&1&0\\ 1&0&1&0&0&0\\ 0&1&0&0&1&0\\ 1&1&0&1&0&0\\ 0&0&0&0&0&0 \end{bmatrix} r(R)=\begin{bmatrix} 0&0&0&0&1&0\\ 0&0&0&0&1&0\\ 1&0&1&0&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{bmatrix} t(R)=⎣⎢⎢⎢⎢⎢⎢⎡101000010000001000000100110110000001⎦⎥⎥⎥⎥⎥⎥⎤s(R)=⎣⎢⎢⎢⎢⎢⎢⎡001010000110101000010010110100000000⎦⎥⎥⎥⎥⎥⎥⎤r(R)=⎣⎢⎢⎢⎢⎢⎢⎡001000000000001000000000110100000000⎦⎥⎥⎥⎥⎥⎥⎤
r(R)步骤和第5题一致
第七题 求关系图等价类
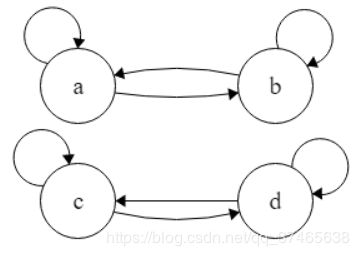
由关系图可知
A0={a,b},A1={c,d}所组成的所有序偶都在R中
所以R的等价类有A0,B0
第八题 写出序偶与哈斯图
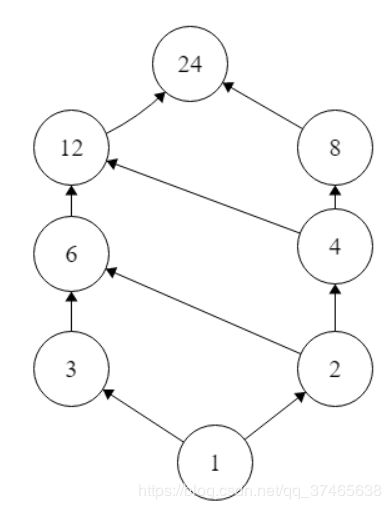
(1) R={
<1,1><1,2>,<1,3>,<1,4>,<1,6>,<1,8>,<1,12>,<1,24>
<2,2><2,4>,<2,6>,<2,8>,<2,12>,<2,24>
< 3,3>,< 3,6>,< 3,12>,< 3,24>,<4,4>,<4,8>,<4,12>,<4,24>
<6,6>,<6,12>,<6,24>,<8,8>,<8,24>,<12,12>,<12,24>,<24,24>
}
注:假装没有看到箭头
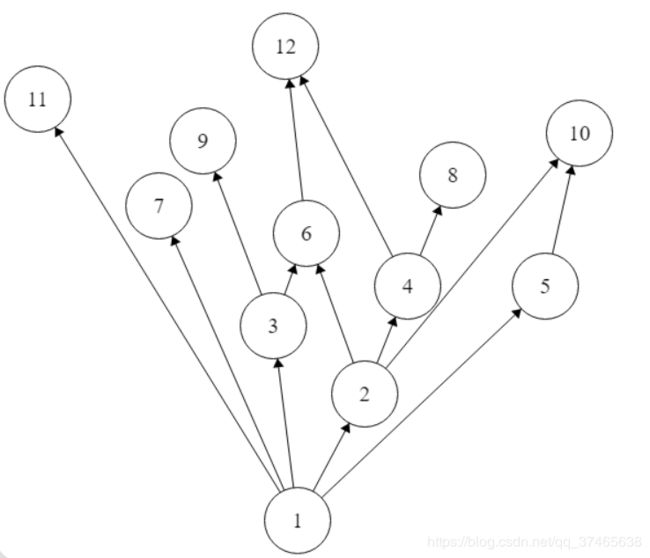
(2)
R={
<1,1>,<1,2>,<1,3>,<1,4>,<1,5>,<1,6>,<1,7>,<1,8>,<1,9>,<1,10>,<1,11>,<1,12>
<2,2><2,4>,<2,6>,<2,8>,<2,12>,< 3,3>,< 3,6>,< 3,9>,< 3,12>
<4,4>,<4,8>,<4,12>,<5,5>,<5,10>,<6,6>,<6,12>
<7,7>,<8,8>,<9,9>,<10,10><11,11>,<12,12>
}