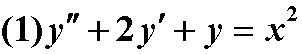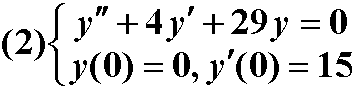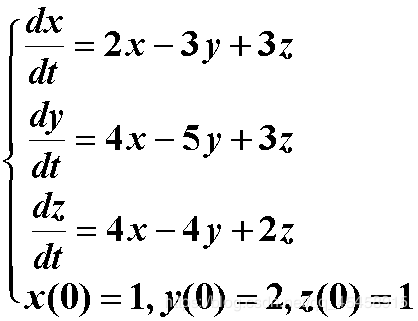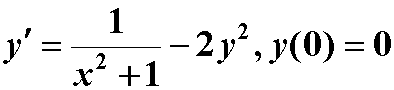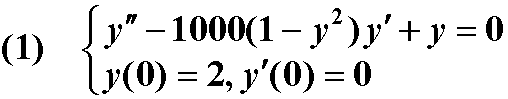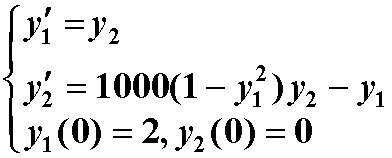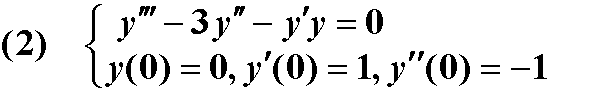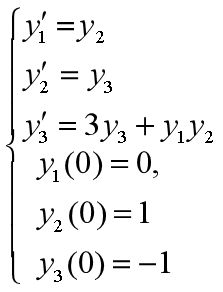MATLAB求解微分方程

一、微分方程的符号解

dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’）

初始条件省缺时，是求微分方程的通解。

Dy代表y的导数，D2y代表y的二阶导数， D3y代表y的三阶导数……

例1：求解微分方程：

解：

y=dsolve('D2y-2*Dy+y-x^2=0','x')

例2：

解：

y=dsolve('D2y+4*Dy+29*y','y(0)=0,Dy(0)=15','x')

例3：求解微分方程组的初值问题

解：

eq1='Dx=2*x-3*y+3*z';
eq2='Dy=4*x-5*y+3*z';
eq3='Dz=4*x-4*y+2*z';
[x,y,z]=dsolve(eq1,eq2,eq3,'x(0)=1,y(0)=2,z(0)=1');%如果省略自变量，默认为t

二、求微分方程数值解

多数微分方程是没有解析解的，即使一些看上去形式非常简单的微分方程，如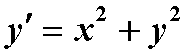，这个微分方程不能用初等函数及其积分来表达它的解！从实际问题中抽象出来的微分方程，通常主要依靠数值解法来解决！求数值解的方法有欧拉法、龙格-库塔法等。基于龙格-库塔法，matlab求微分方程数值解函数：[x, y]=ode23(‘函数’,‘求解区间’,‘初始值’)x: 自变量值，y: 函数值，（采用2,3阶龙格-库塔法）其它求解命令：ode45,ode15s,ode23s等

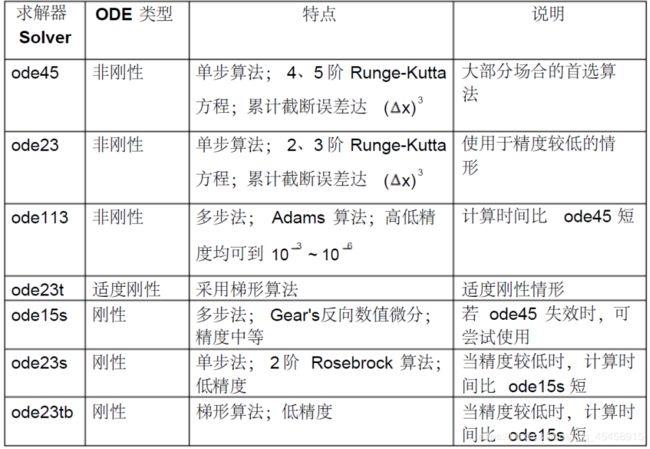
几种常用的求解函数的特点和类型：

关于何为刚性方程： 

所谓刚性方程，就是说存在两(多)重尺度，一个尺度比另外一个尺度大很多。所导致的麻烦就是在计算中很难兼顾两者。

例如下面的方程：
dx=-100x-100.1y 
dy=100.1x-100y 

两个特征值lambda_1 = -200.1，lambda_2 = -0.1 
所以解表现为a1*exp(-200.1*X) + a2*exp(-0.1*X)，无论你用什么样的尺度(单一尺度)都不能很好刻画解的行为。一个是快变行为，一个是慢变行为。 所有这样的方程计算时候，稳定性条件比较苛刻。实际情况要比这还复杂得多。 

一、微分方程求解步骤：

 ：

1. 定义函数 f(x, y)（主要用匿名函数定义）
2. 使用ode函数求解
3. 作图

例4：求解微分方程：

解：

f=@(x, y)1./(1+x.^2)-2*y.^2 
ode23(f, [0, 6], 0)
figure(2) 
ode45(f, [0,6], 0)

二、对于微分方程组：

：

1. 用function函数定义该微分方程组的右端项

   格式：function res=fun(t, x)

   res=[f1(…); f2(…);….;fm(…)];

   end

   其中res为列向量。

2. 使用ode函数求解
3. 作图

例5：求解微分方程初值问题：

解：

[t, x] = ode45(@fun,[0,30],[1,0.5]);
plot(t, x(:,1), t, x(:,2),'linewidth',1.5);
legend('x(t)', 'y(t)');
figure(2);
plot(x(:,1), x(:,2), 'linewidth',1.5);

function res=fun(t, x)
    res = zeros(2,1);
    res(1)=-x(1).^3-x(2);
    res(2)=-x(2).^3+x(1);
end

三、高阶微分方程求数值解：

高阶微分方程必须等价的变换成一阶微分方程组，然后求解。

例6：求解微分方程初值问题：

解：设 y1=y , y2=y'=y1' , y2'=y''

问题转换为

[x, y]=ode15s(@fun,[0,3000],[2,0]);
plot(x, y(:,1))

function res=fun(x,y)
    res = zeros(2,1);
    res(1)=y(2);
    res(2)=1000*(1-y(1)^2)*y(2)-y(1);
end

例7：

解：设 y1=y , y2=y' , y3=y''

问题转换为

[x,y]=ode45(@cal,[0 1],[0;1;-1]);
plot(x,y(:,1));

function res=cal(x,y)
    res = zeros(3,1);
    res(1)=y(2);
    res(2)=y(3);
    res(3)=3*y(3)+y(1)*y(2);
end