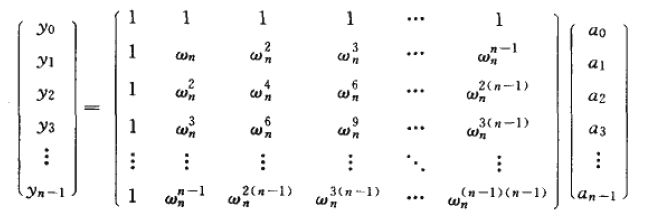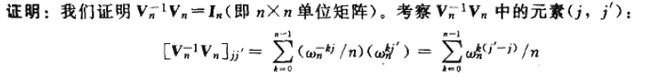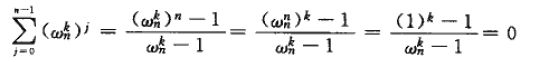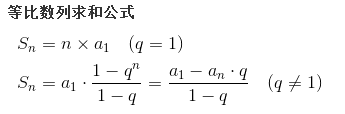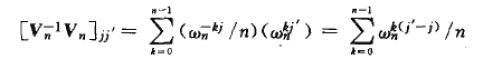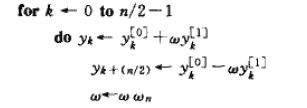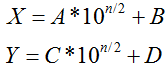大数乘法（快速傅立叶变换）下
大数乘法（快速傅立叶变换）上
上篇已经已经讲了多项式乘法由系数表示法转化为点值表示法（即求值）的FFT算法的过程；接下来讲插值算法，它需不需要用新的算法写一遍呢？并不用这么麻烦！。
我们把DFT写成
，其中
是由
（即主单位复根
，还记得吗？）的适当幂组成的一个范德蒙德矩阵：
对 j, k = 0, 1, ... , n-1 ， 的第 k 行，第 j 列（即(k, j)，理解这个很重要！）处的元素值为
；
则求系数向量 a 的运算为 
。
其中这里有个定理：
不要浮躁，仔细看，能看懂的~
在这里再引入一定理：
求和引理：对任何整数 n >= 1 和不能被 n 整除的非负整数 k，有：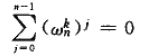
证明：
等比数列求和嘛！给你公式：
之后回来看看这个：
如果 j = j'，则和式的值为1，由求和引理可知在其他情况下和式的值为0.注意，我们依赖-(n - 1) < j' - j < n - 1，以遍 j' - j 不能被 n 整除，这样才能引用求和引理。因此两个矩阵的乘积是单位矩阵。
之后我们就能通过得出：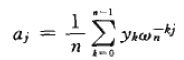
；j = 0, 1, ..., n - 1
看看这样式子跟之前求值的时候的求向量 y 的式子有何区别？
求向量 y 的式子：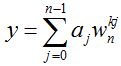
；j = 0, 1, ..., n - 1
我们发现通过对FFT算法进行如下修改：把 a 与 y 的角色互换，用
来代替，并且将每个结果元素除以 n，就可以计算出逆DFT。因此，同样可以在 O(n*logn) 的时间内计算出逆DFT。
于是，通过运用 FFT 与逆FFT，就可以在 O(n*logn) 的时间内，把次数界为 n 的多项式在其系数表示与点值表示之间来回进行转换。
-----------------------------------------------------------------------------------------------------------------------------------------------------
由于DFT的实际应用（如信号处理）需要极高的速度，我们有必要把递归的FFT算法改写成迭代并进行适当的优化以提高速度。
在过程 RECURSIVE-FFT 中的代码：
的值被计算了两次，在编译术语中，该值称为公用子表达式。我们可以使用临时变量 t ，使得它只被计算一次：
接下来看看 n = 8 时 RECURSIVE-FFT 调用形成的递归树：
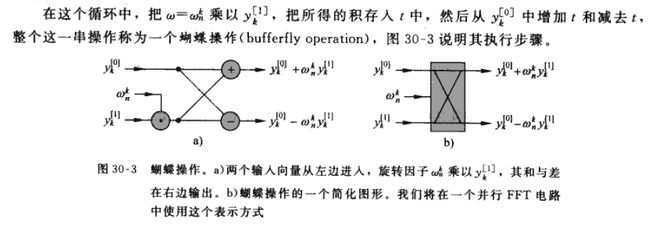
下面要进行截图了，为什么呢？我不能讲的比它更清晰：（《算法导论（第二版第30章）》）
这就是FFT算法的一种迭代实现，至此已经把多项式乘法的快速傅立叶变换全部讲完！
这跟大数乘法有何关系？其实还真有关系，我们看看最开始的例子：
A = 7x^3 + 5x^2 + 3x + 4
B = 4x^2 + 6
C = A * B
7x^3 + 5x^2 + 3x + 4
4x^2 + 6
---------------------------------------
+42x^3 + 30x^2 + 18x + 24
28x^5 + 20x^4 +12x^3 + 16x^2
-----------------------------------------------------------
28x^5 + 20x^4 + 54x^3 + 46x^2 + 18x + 24
则
c[] = {24,18,46, 54, 20, 28, 0, 0}
最后只需要从左向右进位就行了。
这就是大数乘法的快速傅立叶变换的过程！
---------------------------------------------------------------------------------------------------------------------------------------------------------
再啰嗦一点，大数乘法还有一种比 FFT 慢但比直接模拟快的算法，这种算法也运用了分治策略！
X = 2370024
Y = 232
同样我们也把 A , B 的长度通过往后面添加 0，弄成 2 的幂，最后结果再把添加的 0 去掉就行了
X = 23700240
Y = 23200000
则两数的长度都为 n = 8。
那我们可以写成
即 A = 2370, B = 0240（即24）, C = 2320, D = 0000（即0）
A, B, C, D 长度都为 n/2
我们展开得：
在这里请移步学习解递归方程的主定理，了解过后再往下看
这样，长度为 n 的两个数 X, Y的乘积，被分解为长度为 n/2 的 4 对数 {A, C} {A, D} {B, C} {B, D} 的乘积；其中10^k 只是需要往后面添加 0，所以得到递归方程：T(n) = 4T(n/2) + cn；（其中 c 为常数）用主定理解之得 T(n) = O(n^2)，然而并没得到优化。
接下来我们把 AD + BC 进行适当的代数变换得到 AD + BC = (A - B)(D - C) + AC + BD。
这样得：
看起来是复杂了，但实际上它把长度为 n 的两个数 X, Y的乘积，分解为长度为 n/2 的 3 对数{A, C} {(A - B), (D - C)} {B, D} 的乘积；所以得到递归方程：T(n) = 3T(n/2) + cn；（其中 c 为常数）用主定理解之得 T(n) = O(n^(log3)) （其中 log3 是以 2 为底） 约为 T(n) = O(n^(1.59))
这种分治法理解起来比 FFT 简单得多，但实现起来很麻烦，涉及到大数加减法，还需要很大的额外空间储存临时结果，自己试着写过，并没有成功，也觉得实用性不强。。。
结尾献上 FFT 解大数乘法的 C 语言代码（同时这是 HDU 1402 的解答）：
迭代比递归快了不少，另外 C89标准的编译器可能不能通过，C99的就可以；主要还是不太习惯把变量都声明在前面。。。
递归型：
#include
#include
#include
#include
#include
#include
#define N 150010
const double pi = 3.141592653;
char s1[N>>1], s2[N>>1];
double rea[N], ina[N], reb[N], inb[N], Retmp[N], Intmp[N];
int ans[N>>1];
void FFT(double *reA, double *inA, int n, int flag)
{
if(n == 1) return;
int k, u, i;
double reWm = cos(2*pi/n), inWm = sin(2*pi/n);
if(flag) inWm = -inWm;
double reW = 1.0, inW = 0.0;
/* 把下标为偶数的值按顺序放前面，下标为奇数的值按顺序放后面 */
for(k = 1,u = 0; k < n; k += 2,u++){
Retmp[u] = reA[k];
Intmp[u] = inA[k];
}
for(k = 2; k < n; k += 2){
reA[k/2] = reA[k];
inA[k/2] = inA[k];
}
for(k = u,i = 0; k < n && i < u; k++, i++){
reA[k] = Retmp[i];
inA[k] = Intmp[i];
}
/* 递归处理 */
FFT(reA, inA, n/2, flag);
FFT(reA + n/2, inA + n/2, n/2, flag);
for(k = 0; k < n/2; k++){
int tag = k+n/2;
double reT = reW * reA[tag] - inW * inA[tag];
double inT = reW * inA[tag] + inW * reA[tag];
double reU = reA[k], inU = inA[k];
reA[k] = reU + reT;
inA[k] = inU + inT;
reA[tag] = reU - reT;
inA[tag] = inU - inT;
double rew_t = reW * reWm - inW * inWm;
double inw_t = reW * inWm + inW * reWm;
reW = rew_t;
inW = inw_t;
}
}
int main()
{
#if 0
freopen("in.txt","r",stdin);
#endif
while(~scanf("%s%s", s1, s2)){
memset(ans, 0 , sizeof(ans));
memset(rea, 0 , sizeof(rea));
memset(ina, 0 , sizeof(ina));
memset(reb, 0 , sizeof(reb));
memset(inb, 0 , sizeof(inb));
/* 计算长度为 2 的幂的长度len */
int i, lent, len = 1, len1, len2;
len1 = strlen(s1);
len2 = strlen(s2);
lent = (len1 > len2 ? len1 : len2);
while(len < lent) len <<= 1;
len <<= 1;
/* 系数反转并添加 0 使长度凑成 2 的幂 */
for(i = 0; i < len; i++){
if(i < len1) rea[i] = (double)s1[len1-i-1] - '0';
if(i < len2) reb[i] = (double)s2[len2-i-1] - '0';
ina[i] = inb[i] = 0.0;
}
/* 分别把向量 a, 和向量 b 的系数表示转化为点值表示 */
FFT(rea, ina, len, 0);
FFT(reb, inb, len, 0);
/* 点值相乘得到向量 c 的点值表示 */
for(i = 0; i < len; i++){
double rec = rea[i] * reb[i] - ina[i] * inb[i];
double inc = rea[i] * inb[i] + ina[i] * reb[i];
rea[i] = rec; ina[i] = inc;
}
/* 向量 c 的点值表示转化为系数表示 */
FFT(rea, ina, len, 1);
for(i = 0; i < len; i++){
rea[i] /= len;
ina[i] /= len;
}
/* 进位 */
for(i = 0; i < len; i++)
ans[i] = (int)(rea[i] + 0.5);
for(i = 0; i < len; i++){
ans[i+1] += ans[i] / 10;
ans[i] %= 10;
}
int len_ans = len1 + len2 + 2;
while(ans[len_ans] == 0 && len_ans > 0) len_ans--;
for(i = len_ans; i >= 0; i--)
printf("%d", ans[i]);
printf("\n");
}
return 0;
}
迭代型：
#include
#include
#include
#include
#include
#include
#define N 150010
const double pi = 3.141592653;
char s1[N>>1], s2[N>>1];
double rea[N], ina[N], reb[N], inb[N];
int ans[N>>1];
void Swap(double *x, double *y)
{
double t = *x;
*x = *y;
*y = t;
}
int Rev(int x, int len)
{
int ans = 0;
int i;
for(i = 0; i < len; i++){
ans <<= 1;
ans |= (x & 1);
x >>= 1;
}
return ans;
}
void FFT(double *reA, double *inA, int n, bool flag)
{
int s;
double lgn = log((double)n) / log((double)2);
int i;
for(i = 0; i < n; i++){
int j = Rev(i, lgn);
if(j > i){
Swap(&reA[i], &reA[j]);
Swap(&inA[i], &inA[j]);
}
}
for(s = 1; s <= lgn; s++){
int m = (1< len2 ? len1 : len2);
while(len < lent) len <<= 1;
len <<= 1;
for(i = 0; i < len; i++){
if(i < len1) rea[i] = (double)s1[len1-i-1] - '0';
if(i < len2) reb[i] = (double)s2[len2-i-1] - '0';
ina[i] = inb[i] = 0.0;
}
FFT(rea, ina, len, 0);
FFT(reb, inb, len, 0);
for(i = 0; i < len; i++){
double rec = rea[i] * reb[i] - ina[i] * inb[i];
double inc = rea[i] * inb[i] + ina[i] * reb[i];
rea[i] = rec; ina[i] = inc;
}
FFT(rea, ina, len, 1);
for(i = 0; i < len; i++)
ans[i] = (int)(rea[i] + 0.4);
for(i = 0; i < len; i++){
ans[i+1] += ans[i] / 10;
ans[i] %= 10;
}
int len_ans = len1 + len2 + 2;
while(ans[len_ans] == 0 && len_ans > 0) len_ans--;
for(i = len_ans; i >= 0; i--)
printf("%d", ans[i]);
printf("\n");
}
return 0;
}