高程
大地测量学是运用数学工具研究地球的大小和形状,以及表示其表面位置的多种坐标系统的学科。这里有三个基本的表面是需要我们知道的,即:地形实际表面、大地水准面(Geoid)、参考椭球面(Ellipsoid)。
大地水准面是一个非常接近海平面并且具有相同重力势能的表面,如果一个人能够挖掘一条切断陆地、连接起海洋的运河的话,那么这个运河的水面也就是大致的大地水准面。大地水准面是波动的,有的地区高些,有的地区低些,差别甚至可以达到1000公里距离相差100米(注:美国新墨西哥州的Carlsbad就是这样的)。由于重力矢量(vector)总是垂直(perpendicular)于大地水准面的,铅垂线(plumb lines)和水准仪(spirit levels)的工作会受到大地水准面的直接影响。相对于大地水准面的高程称作正高(Orthometric Height),也因为大地水准面与平均海水面大致接近,在使用中,正高和相对于平均海水面(Mean Sea Level,MSL)的高程是可以互换的。
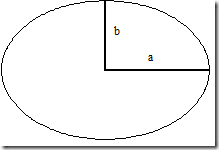
计算大地水准面复杂而困难,因此就要定义其他不那么复杂、又能尽可能描述地球的表面。椭球(ellipsoid)是椭圆(ellipse)绕其短轴旋转所形成的面,在数学上用其长半轴(a)和短半轴(b)来定义,也可以用偏心率倒数(reciprocal of flattening,a/(a-b))和短半轴来定义。椭球在是一个在数学上相对简单的表面,在其之上的距离、方位及位置都是可以计算的。
虽然大量的天文观测以及近年来确定的大量椭球参数(绝对重力测量方法)用于地区级和全球级的应用,椭球面仍然应该是在某一目标区域内大地水准面的最佳。
椭球面和大地水准面是两个完全不同的面,也由于大地水准面的波动性,两者之间的差异也是随地区变化的,这种差异用N表示(注:N为大地水准面差异),如下图:
如椭球高(ellipsoid height)用h表示,正高(Orthometric height)用H表示,那么二者关系可以用这个公式表示:h=H+N。这是一个简单但十分重要的公式。该公式说明:椭球高等于平均海水面高程加上大地水准面差异(ellipsoid/geoid separation)。路易斯安那州/德克萨斯州地区的N值是-25米,这意味着这个地区的大地水准面比椭球面低25米。
GPS接收机工作时得到的高程是基于WGS84(World Geodetic System 84)椭球的椭球高(注:即大地高)。假设我们在差分参考站输入了天线正确的椭球高(注:大地高),那么GPS流动站(rover)结果也是正确的。然而提交的物探数据格式坐标的高程是正高(注:海拔高)。所以,在提供高程之前,我们要用这个公式:H=h-N,转换WGS84的椭球高(注:大地高)为正高(注:海拔高)。
确定某一区域的N值来完成上述转换貌似不可能,但实际上可以。同样,绝对重力测量(用于确定最佳全球性椭球及其与大地水准面的关系)可获得N值。事实上,有不少使用重力势能模型(有时是其他重力测量方法)的软件可以准确的计算出WGS84椭球上点位的N值。输入WGS84点位后,这些软件就能将WGS84椭球高转化为希望的正高。
-----------------------------------------------
原文:
Heights
Geodesy is that part of applied mathematics that deals with the size and shape of the earth and the various coordinate systems that are used to represent a position on its surface. There are actually three primary surfaces with which we must deal. Those are the actual or topographical surface, the geoid, and the ellipsoid.
The geoid is a surface of equal gravity potential which closely matches the surface of the sea. It would also be approximated by the water surface that would develop if one could cut into the continents with canals that were connected to the sea. The geoid is undulating and is characterized by regional highs and lows which can vary (relatively) by as much as 100 meters over a distance of 1000 kilometers. Plumb lines and spirit levels are directly affected by the geoid since the gravity vector is perpendicular to its surface. Heights expressed relative to the geoid are termed orthometric heights, and since the geoid approximates mean sea level, the term orthometric height and the term height above mean sea level are used interchangeably.
Since any computations on the geoid would be difficult if not impossible, another less complex surface which adequately describes the earth must be defined. The ellipsoid is the surface developed by rotating an ellipse around its minor axis. It is defined mathematically by a semi-major (a in the diagram at left) and semi-minor axis (b). Alternatively, the value resulting from the equation, a/a-b is called the reciprocal of flattening, and is often used with the semi-major axis to define the ellipsoid. The ellipsoid is a relatively simple mathematical surface on which distance and bearing can be computed and position referenced.
An ellipsoid should be the best representation of the geoid over a desired region. Through astronomical observations and most recently, absolute gravity measurements, numerous sets of ellipsoid constants have been defined for regional and global use.
The ellipsoid and the geoid are two distinctly different surfaces, and because of the undulating nature of the geoid, there are varying differences between the two. These separations are represented by N in the figure below.
If ellipsoid heights are represented by h and orthometric heights by H, the relationship between the two is determined by the equation, h = H + N. This is a simple, yet extremely important formula. The equation states that ellipsoid height equals height above mean sea level plus the ellipsoid/geoid separation. A typical value for N in the Texas/Louisiana area is -25 meters, meaning that the geoid is 25 meters below the ellipsoid.
Heights as reported by GPS receivers operating autonomously are ellipsoid heights referenced to the World Geodetic System 1984 (WGS84) ellipsoid. Assuming we have correctly entered an ellipsoid height for the antenna at our RTK or differential reference station, the same is true for our GPS equipped rovers. Yet the heights as reported in the seismic format coordinate record are orthometric. Therefore, before providing heights, we must convert from WGS84 ellipsoid heights to orthometric heights using the formula, H = h - N.
While it seems like an impossible task to determine what that value of N might be at a particular location in order to make this conversion, it is not. The same absolute gravity measurements used in determining the most suitable dimensions for a globally used ellipsoid and its relationship to the geoid can be used to provide N. In fact, there are several programs which utilize an underlying geopotential model (and in some cases, additional terrestrial gravity measurements) in order to compute N quite accurately with respect to the WGS84 ellipsoid given an input latitude and longitude. Simply put, these programs are used to convert the GPS ellipsoid heights to the orthometric heights we desire.
源文档 <http://blog.sina.com.cn/s/blog_5654be540100o03k.html>