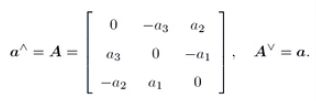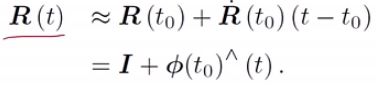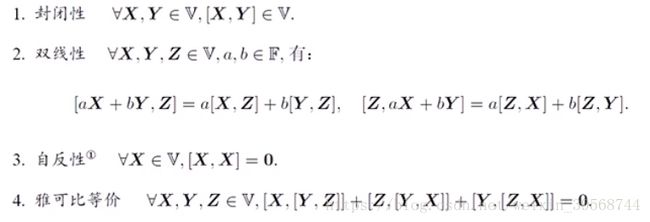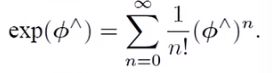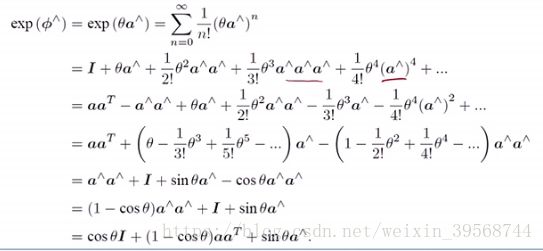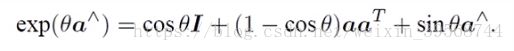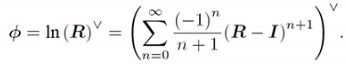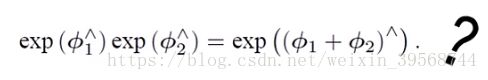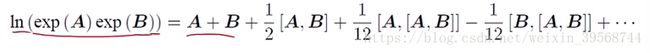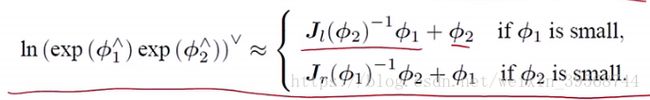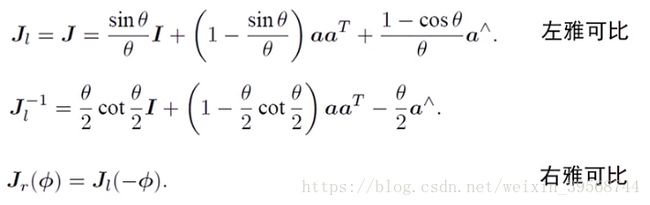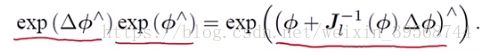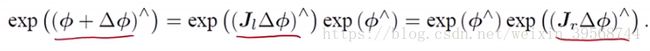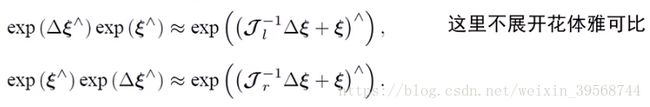李群与李代数基础
最近在学习slam时第一次遇到李群与李代数的概念,由于一开始不太理解,所以想通过这篇笔记来重新归纳梳理一下。
1.李群的概念:
李群是具有连续(光滑)性质的群;它既是群也是流行;直观上看,一个刚体能够连续的在空间中运动,故SO(3)和SE(3)都是李群。(注:SO(3)是特殊正交群 SE(3)是特殊欧式群,由于旋转矩阵R是3乘3的维度,但自由度的约束只有3个自由度,所以旋转矩阵R在9维空间中是一个连续的3维曲面或流形)但是,SO(3)和SE(3)只有定义良好的乘法,没有加法,所以难以进行取极限和求导等操作。 但能不能做一些近似或分析上的事情呢?下面来看李代数的概念。
2.李代数的概念:
李代数是与李群对应的一种结构,位于向量空间。通常通常记作小写的so(3)和se(3),事实上李代数是李群单位元处的正切空间。
切空间本身是一个向量空间,所以切空间就可以定义很好的加法运算了。由此可以借由李代数这个切空间去研究对应的李群的一些性质。
例如:大写的SO(3)是一个李群(流形、曲面),他上面的点无法定义加法运算,因为曲面上的两个点相加后可能就不在这个曲面上了。在SO(3)这个曲面上某个点处可以做它的一个切平面似的东西或者叫做切空间,这个切空间(是一个平面)就是对应的李代数,记作小写的so(3).
3.下面从旋转矩阵引出李代数
考虑任意旋转矩阵R,满足![]() 考虑旋转随时间变化(连续运动),则有
考虑旋转随时间变化(连续运动),则有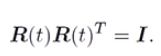
记作:![]() 两边右乘R(t)可得:
两边右乘R(t)可得:![]() ,这个式子看起来很像对R(t)求导数后左边多出了一个
,这个式子看起来很像对R(t)求导数后左边多出了一个![]() 项;很类似于对标量求导中的指数函数求导。
项;很类似于对标量求导中的指数函数求导。
下面进行更进一步的近似,考虑单位元附近的情况:![]()
由此可见![]() 反映了一阶导数性质,它位于正切空间(tangent space)上。
反映了一阶导数性质,它位于正切空间(tangent space)上。
已知初始情况:R(0)=I,解得:![]() 该式说明対任意的t都能找到一个R和一个
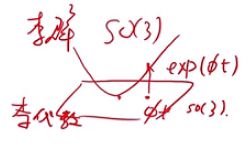
该式说明対任意的t都能找到一个R和一个![]() 的对应关系,该关系称为指数映射(Exponential Map)。可以大致理解为在切空间附近的一个点想要找到对应的李群只要求一次exp就可以了,如下图所示: 这里的
的对应关系,该关系称为指数映射(Exponential Map)。可以大致理解为在切空间附近的一个点想要找到对应的李群只要求一次exp就可以了,如下图所示: 这里的![]() 就称为SO(3)对应的李代数so(3)
就称为SO(3)对应的李代数so(3)
4.李代数(Lie Algebra):
每个李群都有与之对应的李代数。李代数描述李李群单位元附近的正切空间性质。
李代数由一个集合![]() 一个数域
一个数域![]() 和一个二元运算[,]组成。如果它们满足以下几条性质,称(V,F,[,])为一个李代数。
和一个二元运算[,]组成。如果它们满足以下几条性质,称(V,F,[,])为一个李代数。
二元运算[,]被称为李括号,直观上说李括号表达李两个元素的差异。
例子:三维空间向量+叉积运算构成李代数
其中:
同理,SE(3)也有李代数se(3):
5.指数映射和对数映射
指数映射反映李从李代数到李群的对应关系:![]() 、
、
但是![]() 是一个矩阵,对于矩阵,如何定义求指数运算呢?根据微积分中学过的知识,指数计算可以用泰勒展开来写成一个级数形式的样子:
是一个矩阵,对于矩阵,如何定义求指数运算呢?根据微积分中学过的知识,指数计算可以用泰勒展开来写成一个级数形式的样子:
由于![]() 是向量,所以可以将他的模长和方向分离出来,用角度乘单位向量来表示:
是向量,所以可以将他的模长和方向分离出来,用角度乘单位向量来表示:![]()
关于其中的单位向量a可以验证以下的性质:
由此进行泰勒展开:
结果即为:
这个结果与罗德里格斯公式是一致的,这说明so(3)的物理意义就是旋转向量。
反之,给定一个旋转矩阵时,也能求李代数:
下面给出se(3)到SE(3)的指数映射:
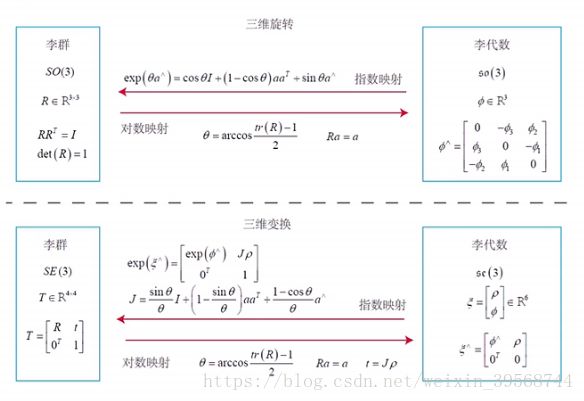
对两个李群总结一下:
6.李代数求导与扰动模型
首先slam的定位就是在对相机进行位姿估计,但李群中没有加法:因为![]() 这就导致导数在李群中无从定义,那么解决的办法是什么呢?一个基本的思想就是:利用李代数上加法定义李群元素的导数,并使用指数映射和对数映射完成变换关系。但这时就有一个基本的问题:当在李代数中作加法时,是否等价于在李群上做乘法?
这就导致导数在李群中无从定义,那么解决的办法是什么呢?一个基本的思想就是:利用李代数上加法定义李群元素的导数,并使用指数映射和对数映射完成变换关系。但这时就有一个基本的问题:当在李代数中作加法时,是否等价于在李群上做乘法?
在使用标量的情况下这个式子明显是成立的,但可惜的是这里的参数是矩阵,所以是不成立的,他多李一些东西。
完整的形式由BCH(Baker-Campbell=Hausdorff)公式给出,完整形式非常复杂,部分展开式如下(方括号为李括号)
当其中一个量为小量时,忽略其高阶项,BCH具有线性近似形式:
其中:
直观写法(以左乘为例)在李群上左乘小量时,李代数上的加法相差左雅可比的逆:
反之,李代数上进行小量加法时,相当于李群上左(右)乘一个带左(右)雅可比的量:
SE(3)比SO(3)更复杂:
通过BCH线性近似,可以定义李代数上的导数,考虑一个基本问题:旋转后的点关于旋转的导数,由于无法定义所以不严谨的记为: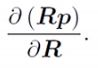
由于R没有加法,导数无从定义,存在两种解决的办法:
a.对R对应的李代数加上小量,求相对于小量的变化率(导数模型);
b.对R左乘或右乘一个小量,求相对于小量的李代数的变化率(扰动模型)
导数模型如下:
扰动模型更加简洁实用,如下:
SE(3)上的扰动模型: