判断点是否在凸多边形内
方法实际有很多,例如
(1)面积和判别法:判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形,相等则在多边形内部。
(2)夹角和判别法:判断目标点与所有边的夹角和是否为360度,为360度则在多边形内部。
(3)引射线法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。
这里我看到一种比较简单的方法,对于凸多边形有效,我记录下。、
1.原理
假设凸多边形顶点,按照顺时针顺序构成顶点数组verts:Point[],依次取两个顶点构成线段序列。
若点落在凸多边形内,则必有:该点在所有的线段序列的右侧或者左侧。
2.概念
右手坐标系
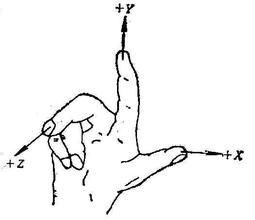
让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指能指向z轴的正方向,则称这个坐标系为右手直角坐标系。反之则是左手直角坐标系。
另一种通俗的理解:
伸出右手,让拇指和食指成“L”形,大拇指向右,食指向上,其余的手指指向前方,这样就建立了一个右手坐标系。其中,拇指、食指和其余手指分别代表x,y,z轴的正方向。
向量点积
向量叉积
这里我们可以用向量叉积,即叉乘做,我们这里可以如下图化简,化简完叉乘的式子就是
![]() ,这里如果这个式子小于0,则在左边,若大于0则在右边,由于是顺时针,所以如果点在多边形内部,应该大于0
,这里如果这个式子小于0,则在左边,若大于0则在右边,由于是顺时针,所以如果点在多边形内部,应该大于0
3.源码
// 是否顺时针
private static isClockwise(a: Point, b: Point, c: Point): boolean {
//取ab向量,ac向量,进行叉乘
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y) < 0;
}
private static isClockwiseMargin(a: Point, b: Point, c: Point): boolean {
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y) <= 0;
}
//verts,六边形的顶点,顺时针存储
private static inConvexPolygon(p: Point, verts: Point[]): boolean {
if (verts.length < 3) {
return false;
}
let iniResult = this.isClockwise(verts[0], verts[1], p);
for (let i = 1; i < verts.length; i++) {
let p1 = verts[i];
let p2 = null;
if (i == verts.length - 1) {
p2 = verts[0];
}
else {
p2 = verts[i + 1];
}
if (this.isClockwise(p1, p2, p) != iniResult) {
return false;
}
}
return true;
}
另一种来自googleInterview的实现:
https://yuanhsh.iteye.com/blog/2222040
// 是否顺时针
private static isClockwise(a: Point, b: Point, c: Point): boolean {
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y) < 0;
}
private static isClockwiseMargin(a: Point, b: Point, c: Point): boolean {
return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y) <= 0;
}
private static inConvexPolygon(p: Point, verts: Point[]): boolean {
if (verts.length < 3) {
return false;
}
if (this.isClockwise(verts[0], p, verts[1])) return false;
if (this.isClockwise(verts[verts.length - 1], p, verts[0])) return false;
let i = 2, j = verts.length - 1;
let line = -1;
while (i <= j) {
let mid = (i + j) >> 1;
if (this.isClockwiseMargin(verts[0], p, verts[mid])) {
line = mid;
j = mid - 1;
}
else {
i = mid + 1;
}
}
return this.isClockwise(verts[line], p, verts[line - 1]);
}
转自:https://blog.csdn.net/iningwei/article/details/86474042