DAG最长路

0. 引言

在图的专题的学习里面，我们讲述了如何求解AOE网的最长路径，但是求解的方法比较苦涩难懂，对初学者不太友好（当然，对我这种大一学了数据结构，大二学了算法，大三还是看不懂的人一样不友好惹）。而且很多问题都可以转换成求解DAG上的最长或最短路径问题。所以，求解DAG上的最长或最短路径问题很重要。

下面介绍一种更简便的方法。由于DAG最长路和最短路的思想是一致的，因此下面以最长路为例。

（通过本节的学习，你应该要知道如何求DAG的最长路和最短路(●ˇ∀ˇ●)）

本节着重解决两个问题：

1. 求整个DAG中的最长路径（即不固定起点或终点）；
2. 固定终点，求DAG的最长路径。

1. 求整个DAG中的最长路径（即不固定起点或终点）

先讨论第一个问题：给定一个DAG，怎样求解整个图的所有路径中权值之和最大的那条。

如图11-6所示，路径(B,D,F,I)就是该图的最长路径，长度为9。

问题1：如何定义状态？

令 dp[i]表示从i号顶点出发能获得的最长路径长度 。
我们知道一条路径一定是有起点的，那么DAG中最长的路径也肯定是有起点的，这样所有 dp[i] 的最大值就是整个DAG的最长路径长度。

问题2：如何求解dp数组？

注意到 dp[i] 表示从i号顶点出发能获得的最长路径长度，如果从i号顶点出发能到达顶点$j_1$、$j_2$、…、$j_k$，而$dp[j_1]$、$dp[j_2]$、…、$dp[j_k]$均未知，那么就有 dp[i] = max{dp[j]+length[i→j]|(i,j) ∈ E}，如下图所示：

由于动态规划有递推和递归两种实现方式，接下来我们分别来看一下：

解法1：递推——逆拓扑序列

可以按照逆拓扑序列的顺序来求解dp数组。
所谓逆拓扑排序应该就是记录的是 OutDegree 数组，而不是 InDegree 数组。最先将出度为0的点入队列。

解法2：递归——记忆化搜索

有没有办法不求出逆拓扑序列也能计算dp数组的方式呢？
当然，那就是记忆化搜索。

代码如下，其中使用邻接矩阵的方式来存储图：

int DP(int i){
	if(dp[i] > 0) return dp[i];	//dp[i]已计算得到
	//这里面包含了递归边界。
	for(int j=0;j<n;j++){	//遍历i的所有出边 
		if(G[i][j] != INF){
			dp[i] = max(dp[i],DP(j)+G[i][j]);
		}
	}
	return dp[i];	//返回计算完毕的dp[i] 
}

由于从出度为0的顶点出发的最长路径长度为0，因此边界为这些顶点的dp值为0.但具体实现时不妨对整个dp数组初始化为0，这样DP函数当前访问的顶点i的出度为0时就会返回dp[i]=0（以此作为dp的边界），而出度不是0的顶点则会递归求解，递归过程中遇到已经计算过的顶点则直接返回对应的dp值，于是从程序逻辑上按照了逆拓扑序列的顺序进行。

问题3：如何记录最长路径上的顶点？

回忆在Dijkstra算法中使用pre数组来保存每个顶点的前驱结点。事实上，可以把这种想法用到这里——开一个int型choice数组记录最长路径上顶点的后继结点。

注意：如果最终可能有多条最长路径，将choice数组改为vector类型的数组即可。

代码如下：

int DP(int i){
	if(dp[i] > 0 )  return dp[i];	//dp[i]已计算得到
	for(int j=0;j<n;j++){	//遍历i的所有出边 
		if(G[i][j] != INF){
			int temp = DP(j) + G[i][j];	//单独计算，防止if中调用
			if(temp > dp[i]){	//可以获得更长的路径 
				dp[i] = temp;	//覆盖dp[i]
				choice[i] = j;	//i号顶点的后继顶点是j 
			} 
		} 
	}
	return dp[i];	//返回计算完毕的dp[i] 
}

//调用printPath前需要先得到最大的dp[i],然后将i作为路径起点传入
void printPath(int i){
	printf("%d",i);
	while(choice[i] != -1){	//choice数组初始化为-1 
		i = choice[i];
		printf("->%d",i); 
	}
} 

⭐⭐⭐⭐⭐
对一般的动态规划问题而言，如果需要得到具体的最优方案，可以采用类似的方法，即记录每次决策所选择的策略，然后在dp数组计算完毕后根据具体情况进行递归或者迭代来获取方案。读者不妨思考一下，如何对前几个小节的问题求解最优方案。
⭐⭐⭐⭐⭐

更进一步，模仿字符串来定义路径序列的字典序：如果有两条路径$a_1$→$a_2$→…→$a_m$与$b_1$→$b_2$→…→$b_n$，且$a_1$=$b_1$、$a_2$=$b_2$、…、$a_k$=$b_k$、$a_{k+1}$<$b_{k+1}$，那么称路径序列$a_1$→$a_2$→…→$a_m$的字典序小于路径$b_1$→$b_2$→…→$b_n$。于是以此可以提出一个问题：如果DAG中有多条最长路径，如何选择字典序最小的那条？

很简单，只需要遍历i的邻接点的顺序从小到大即可 （事实上，上面的代码自动实现了这个功能(●ˇ∀ˇ●)）

---

至此，都是令dp[i]表示从i号顶点出发能获得的最长路径长度。那么，如果令dp[i]表示以i号结点结尾能获得的最长路径长度，又会有什么结果呢？

可以想象，只要把求解公式变为dp[i] = max{dp[j] + length[j→i]|(j,i)∈E}（相应的求解顺序变成了拓扑序），就可以同样得到最长路径长度，也可以设置choice数组求出具体方案，但却不能直接得到字典序最小的方案，这是为什么呢？

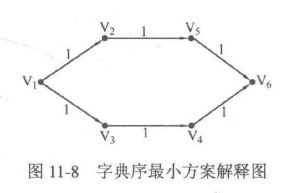
举个简单的例子，如图11-8所示，如果令dp[i]表示从i号顶点出发能获得的最长路径长度，且dp[2]和dp[3]已经计算得到，那么计算dp[1]的时候只需要从$V_2$和$V_3$中选择字典序较小的$V_2$即可；而如果令dp[i]表示以i号顶点结尾能获得的最长路径长度，且dp[4]和dp[5]已经计算得到，那么计算dp[6]时如果选择了字典序较小的$V_4$，则会导致错误的选择结果：理论上应当是$V_1$→$V_2$→$V_5$的字典序最小，可是却选择了$V_1$→$V_3$→$V_4$。

显然，由于字典序的大小总是先根据序列中较前的部分来判断，因此序列中越靠前的顶点，其dp值应当越后计算（对一般的序列型动态规划问题也是如此）。

2. 固定终点，求DAG的最长路径长度

在上面的讨论的基础上，接下来讨论本节开头的第二个问题：固定终点，求DAG的最长路径长度。例如在图11-6中，如果固定H为路径的终点，那么最长路径就会变成B→D→F→H。

有了上面的经验，应当能很容易想到这个延伸问题的解决方案。假设规定的终点为T，那么可以令dp[i]表示从i号顶点出发到达终点T能获得的最长路径长度。

1. 设置vis数组的原因：防止计算过的不能到达终点的点被重复计算。

int DP(int i){
	if(vis[i]) return dp[i];	//dp[i]已计算得到
	vis[i] = true;
	for(int j=0;j<n;j++){
		if(G[i][j] != INF){
			dp[i] = max(dp[i],DP(j) + G[i][j]);
		}
	}
	return dp[i];	//返回计算完毕的dp[i] 
}

至于如何记录方案以及如何选择字典序最小的方案，均与第一个问题相同，此处不再赘述。读者需要思考，如果令dp[i]表示以i号顶点结尾能获得的最长路径长度，应当如何处理？
事实上这样设置dp[i]会变得更容易解决问题，并且dp[T]就是结果，只不过仍然不方便处理字典序最小的情况。

3. 应用场景

至此，DAG最长路的两个关键问题都已经解决，最短路的做法与之完全相同。那么具体什么场景可以应用到呢？

3.1 关键路径

除了10.7.3节介绍的关键路径求解以外，可以把一些问题转换为DAG的最长路，例如经典的矩阵嵌套问题。

3.2 矩阵嵌套问题

矩形嵌套问题：给出n个矩阵的长和宽，定义矩阵的嵌套关系为：如果有两个矩形A和B，其中矩形A的长和宽分别为a、b，矩形B的长和宽分别为c、d，且满足a

这个例子就是典型的DAG最长路问题——将每个矩形都看成一个顶点，并将嵌套关系视为顶点之间的有向边，边权均为1，于是就可以转换为DAG最长路问题。

4. 反思

1. 需要理解：定义dp数组时，使用起点定义和终点定义这两种不同定义的区别。
2. 当要求最小字典序的时候要用起点定义法；
3. 机试不会考你裸的DAG，通常会给你不明显的DAG，然后需要你自己去把其中的物体转换成DAG的顶点，物体之间的关系转换成DAG的边，最值问题变成求DAG最长路径的问题。其实我们的LIS可以转换成DAG问题 ，只不过需要先构造成有向无环图罢了。
4. 只要是求最长的那种问题，都要思考是否可以使用DAG。

5. 题型训练

1. LeetCode 1048. Longest String Chain
   (这个题我没用DAG写，但是它其实是可以用DAG写的，它就是一个有向无环图。)
2. LIS
3. LeetCode 435. Non-overlapping Intervals

6. 参考文档

1. 算法笔记