对鸢尾花数据集和月亮数据集用LDA、k-means和SVM进行二分类可视化分析
一.鸢尾花数据集算法可视化
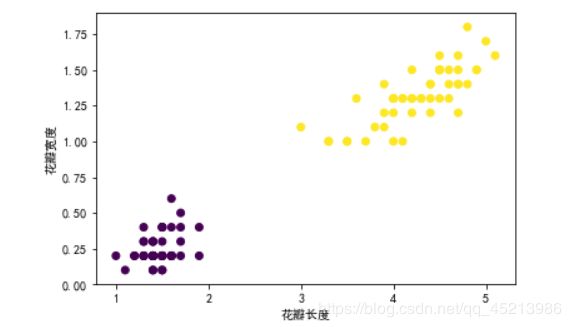
1.LDA对鸢尾花数据集聚类
代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
def LDA(X, y):
#根据y等于0或1分类
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
len1 = len(X1)
len2 = len(X2)
mju1 = np.mean(X1, axis=0)#求中心点
mju2 = np.mean(X2, axis=0)
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2=np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
a=mju1-mju2
a=(np.array([a])).T
#计算w
w=(np.dot(np.linalg.inv(Sw),a))
#计算投影直线
#k=w[1]/w[0]
#b=0;
#x=np.arange(0,5)
#yy=k*x+b
#plt.plot(x,yy)
X1_new =func(X1, w)
X2_new = func(X2, w)
y1_new = [1 for i in range(len1)]
y2_new = [2 for i in range(len2)]
return X1_new,X2_new,y1_new,y2_new
def func(x, w):
return np.dot((x), w)
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # 花瓣长度与花瓣宽度 petal length, petal width
y = iris["target"]
#print(y)
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
#print(Sw)
x1_new, X2_new, y1_new, y2_new = LDA(X, y)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.show()
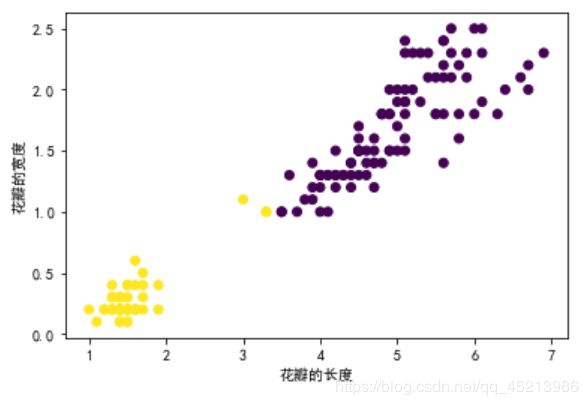
2.k-means对鸢尾花数据集聚类
代码:
from sklearn.cluster import KMeans
#加载数据集
lris_df = datasets.load_iris()
#print(lris_df)
#挑选第2列,花瓣的长度
x_axis = lris_df.data[:,2]
#print(x_axis)
#挑选第三列,花瓣的宽度
y_axis = lris_df.data[:,3]
#print(y_axis)
#这里已经知道了分2类,其他分类这里的参数需要调试
model = KMeans(n_clusters=2)
#训练模型
model.fit(lris_df.data)
prddicted_label= model.predict([[6.3, 3.3, 6, 2.5]])
all_predictions = model.predict(lris_df.data)
#plt.plot(a, b, "bs")
plt.xlabel('花瓣的长度')
plt.ylabel('花瓣的宽度')
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
#打印出来对150条数据的聚类散点图
plt.scatter(x_axis, y_axis, c=all_predictions)
plt.show()
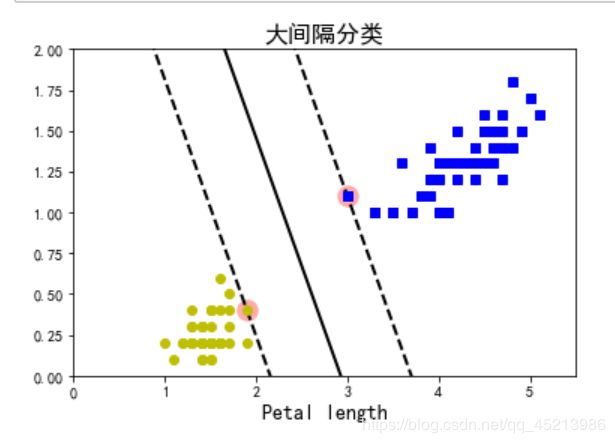
3.SVM对鸢尾花数据集聚类
代码:
from sklearn.svm import SVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # 花瓣长度与花瓣宽度 petal length, petal width
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
# 获取决策边界的w和b
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
# 画中间的粗线
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
# 计算间隔
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
# 获取支持向量
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
plt.title("大间隔分类", fontsize=16)
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()
二.月亮数据集算法可视化
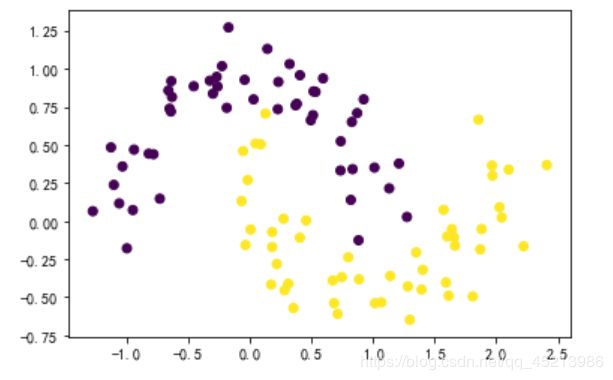
1.LDA对月亮数据集聚类
代码:
def LDA(X, y):
#根据y等于0或1分类
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
len1 = len(X1)
len2 = len(X2)
mju1 = np.mean(X1, axis=0)#求中心点
mju2 = np.mean(X2, axis=0)
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2=np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
a=mju1-mju2
a=(np.array([a])).T
w=(np.dot(np.linalg.inv(Sw),a))
X1_new =func(X1, w)
X2_new = func(X2, w)
y1_new = [1 for i in range(len1)]
y2_new = [2 for i in range(len2)]
def func(x, w):
return np.dot((x), w)
X, y = datasets.make_moons(n_samples=100, noise=0.15, random_state=42)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.show()
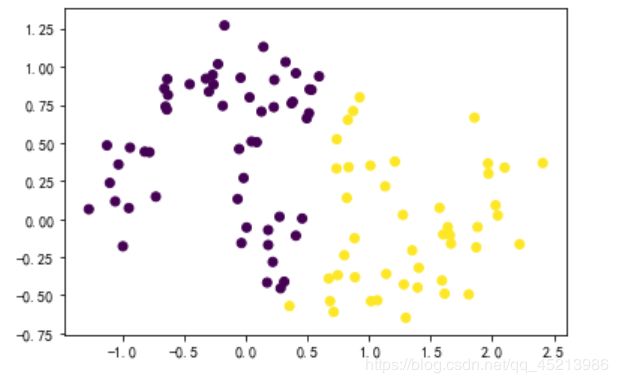
2.k-means对月亮数据集聚类
代码:
from sklearn.datasets import make_moons
from sklearn.cluster import KMeans
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
#X是一个100X2维度的,分别选取两列的数据
X1=X[:,0]
X2=X[:,1]
#这里已经知道了分2类,其他分类这里的参数需要调试
model = KMeans(n_clusters=2)
#训练模型
model.fit(X)
#print(z[50])
#选取行标为50的那条数据,进行预测
prddicted_label= model.predict([[-0.22452786,1.01733299]])
#预测全部100条数据
all_predictions = model.predict(X)
#plt.plot(a, b, "bs")
#打印聚类散点图
plt.scatter(X1, X2, c=all_predictions)
plt.show()
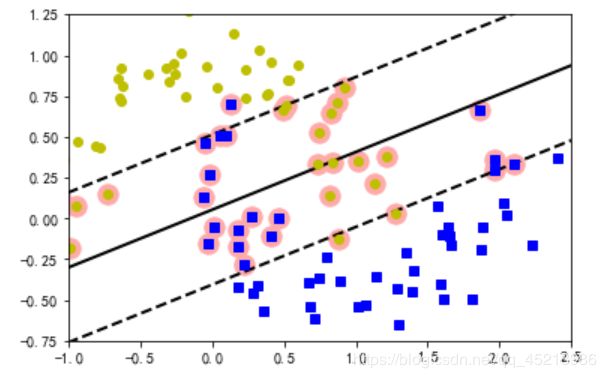
3.SVM对月亮数据集聚类
代码:
X, y = datasets.make_moons(n_samples=100, noise=0.15, random_state=42)
svm_clf = SVC(kernel="linear")
svm_clf.fit(X, y)
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
# 获取决策边界的w和b
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
x0 = np.linspace(xmin, xmax, 200)
# 画中间的粗线
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
# 计算间隔
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
# 获取支持向量
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
plot_svc_decision_boundary(svm_clf, -2, 3)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.axis([-1, 2.5, -0.75, 1.25])
plt.show()
三.SVM算法的优缺点
优点:
1、使用核函数可以向高维空间进行映射
2、使用核函数可以解决非线性的分类
3、分类思想很简单,就是将样本与决策面的间隔最大化
4、分类效果较好
缺点:
1、对大规模数据训练比较困难
2、无法直接支持多分类,但是可以使用间接的方法来做
参考链接,个人博客链接