插值算法

插值算法 什么时候用？

插值算法 是离散函数逼近的重要方法，在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值

插值算法 非常适合在题目给出离散数据时使用，用于补全数据，且样本数据较少的情况（即小于30）

演示插值法在实践中的用途

完成下图数据的插值（补全15周的数据），要求至少选取两种插值方法，并对1号池中的这些指标做出插值后图像

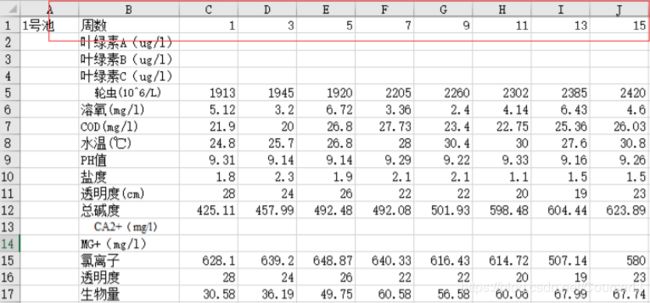
一、将数据导入 Matlab 中（注意不用加文字）

二、运行代码（代码在下面）
数学建模常用的插值法：三次埃尔米特插（Hermite）、三次样条插值法
恰巧这两种插值法在 Matlab 都有内置函数：pchip、spline
只需要导入数据，分别运行插值函数，并各自作图即可

运行结果如下：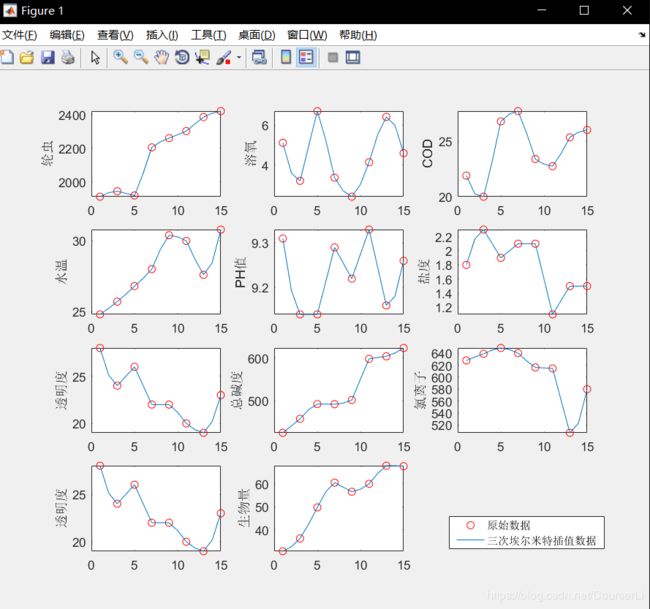

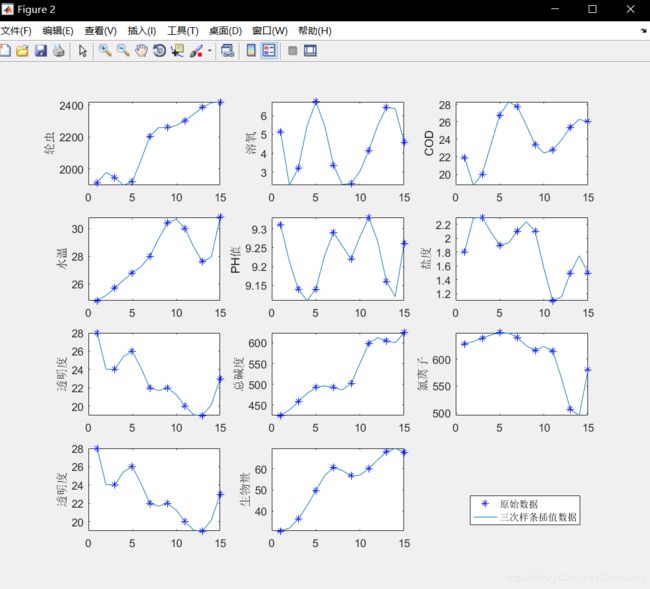
三次埃尔米特插值法 的数据

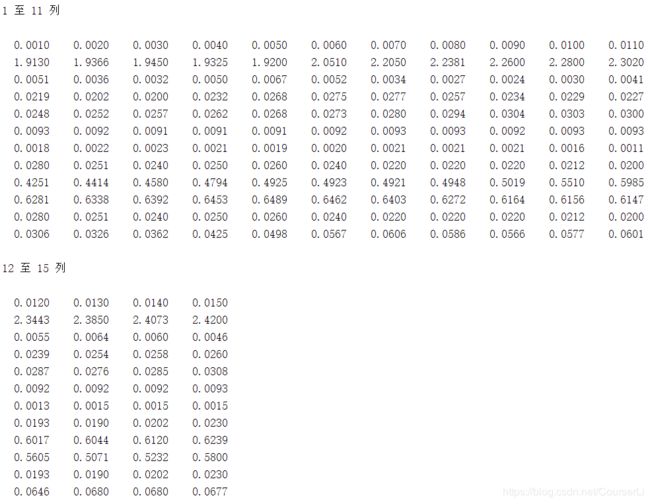
三次样条插值法 的数据

%% 预处理
load Z.mat		 % 导入数据表格 Z
x=Z(1,:); 		 % 第一行表示星期：1  3  5  7  9  11  13  15
[n,m]=size(Z);
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};
P=zeros(11,15);
Q=zeros(11,15);

%% 调用插值法
for i=2:n 			% 从第二行开始都是要进行插值的指标
    y=Z(i,:);		% 将每一行依次赋值给 y
    new_x=1:15;		% 要进行插值的 new_x
    
    % 调用三次埃尔米特插值函数
    p1=pchip(x,y,new_x);			% pchip
    figure(1);
    subplot(4,3,i-1);				% 将所有图依次变现在 4 * 3 的一幅大图上
    plot(x,y,'ro',new_x,p1,'-');	% 画出每次循环处理后的图像
    axis([0 15,-inf,inf])  			% 设置坐标轴的范围，这里设置横坐标轴 0-15，纵坐标不变化
    ylabel(ylab{i})					% y 轴标题
    P(i-1,:)=p1;					% 将每次插值之后的结果保存在 P 矩阵中   
    
    % 调用三次样条插值函数
    p2=spline(x,y,new_x);			% spline 使用原理同上
    figure(2);
    subplot(4,3,i-1);
    plot(x,y,'b*',new_x,p2,'-');
    axis([0 15,-inf,inf])
    ylabel(ylab{i})
    Q(i-1,:)=p2;					% 将每次插值之后的结果保存在 Q 矩阵中  
end

%% 显示插值法数据
legend('原始数据','三次埃尔米特插值数据','Location','SouthEast')
P = [1:15; P]
legend('原始数据','三次样条插值数据','Location','SouthEast')
Q = [1:15; Q]

切记不能直接用于论文中，要根据题目适当的修改，避免查重

关于使用插值法的补充

① 不要把 插值法 写进关键词中
国奖论文几乎没有把插值法放进关键词中的，因为插值法是作为一种方法，用于辅助，而不是一种模型，所以尽量不要放进关键词中

② 了解 插值法 的原理
目的是为了答辩时评委问道，但不用明白太深，理解原理 （会背） 即可

关于：三次
三次是指由分段三次拼接而成的曲线函数

关于：埃尔米特（Hermite）
对于函数 $f(x)$，当我们知道它在一些点处的函数值，而且还能知道它在这些点的导数值时，并且在这些点上的插值函数 $p(x)$ 的函数值和导数值同时满足与 $f(x)$ 的函数值和导数值相等的要求时，此时的问题就是 Hermite 插值问题，也称带有导数的插值问题

关于：样条插值
数学样条这个概念是指在连接点，也就是样点上必须要二阶连续可导，并从数学角度加以归纳得到的，利用样条插值方法得到的插值曲线光滑性好，但却不收敛；但三次样条插值法不仅可以达到函数的收敛性，还可以很好地保持数据光滑性和连续性

插值法的评估

三次埃尔米特插值法 的优点：
该方法,具有很强的适应性和可控性
三次样条插值法 的优点：
该方法不仅可以达到函数的收敛性，还可以很好地保持数据光滑性和连续性，减少信息量的损失
两者插值法 的缺点：
数据量对模型的精度存在一定的限制，若存在更多的数据，训练所得结果会更加贴近实际