- Codeforces Round 972 (Div. 2) A-C 题解
AKDreamer_HeXY
Codeforces比赛题解c++算法动态规划数据结构贪心算法
本来以为B2难度会1900什么的,结果感觉1200还没有,先做的B1,后悔了QwQ关于我现场没切出C这件事……现场排名:A.SimplePalindrome题意构造一个长度为nnn的字符串,只包含aeiou五种字母,需要使得构造出来的字符串所包含的回文子序列数量最小思路当n≤5n\le5n≤5时,只要555个字母不重复出现都是最优情况当n>5n>5n>5时,可以证明:把相同字母放在一起是最优情况:
- Codeforces Round 969 (Div. 2) C. Dora and C++ (裴蜀定理)
致碑前繁花
刷题记录c语言c++开发语言
什么?竟然是裴蜀定理。。。由于这里给出了a和b两个数,我们或许可以想到使用同样是需要给出两个定值的裴蜀定理,即:如果给定xxx和yyy,那么一定有ax+by=gcd(x,y)ax+by=gcd(x,y)ax+by=gcd(x,y)。所以在这时候我们就可以让输入的所有数都去对gcd(a,b)gcd(a,b)gcd(a,b)取模,这样就能够得到所有数的最简形式(可以当成是让所有数尽可能消去aaa和bb
- Codeforces Round #956 (Div. 2) C. Have Your Cake and Eat It Too
abTao_lx
c语言算法开发语言
CodeforcesRound#956(Div.2)C.HaveYourCakeandEatItToo题目大意:有长度为nnn的数组a,b,ca,b,ca,b,c,三个数组的和相同,把nnn分为三段非空连续段[la,ra],[lb,rb],[lc,rc][l_a,r_a],[l_b,r_b],[l_c,r_c][la,ra],[lb,rb],[lc,rc],互不重合。保证∑i=laraai,∑i=
- Codeforces Round #787 (Div. 3)个人题解
旋转卡题
算法贪心算法图论动态规划
CodeforcesRound#787(Div.3)个人题解文章目录CodeforcesRound#787(Div.3)个人题解A.FoodforAnimals题目大意思路参考代码B.MakeItIncreasing题目大意思路参考代码C.DetectiveTask题目大意思路参考代码D.VerticalPaths题目大意思路参考代码E.ReplaceWiththePrevious,Minimiz
- Codeforces Round 966 (Div. 3) ABCDEF
菜比乌斯反演
Codeforces算法c++数据结构
A题:PrimaryTask题意Dmitry写了t个整数,但是在写幂的时候写错了,将^符号给省略掉了。问哪几个是写幂时写错的思路写错的数符合10X,其中X(X>=2)是不含前导零的正整数,我们依此进行判断即可。代码inlinevoidsolve(){strings;cin>>s;intn=s.size();if(n='2'||n>3&&s[2]!='0')cout>n;vectorvis(n+2)
- 程序员进阶之算法练习(四十)Codeforces
落影loyinglin
正文题目1题目链接题目大意:在一维坐标轴上有三个点,坐标是a、b、c;现在需要移动这三个点的位置,使得三个点之间两两间隔大于d;每次只能移动一个点,每秒只能移动距离1;问最少需要多少秒,才能满足要求。输入:一行,四个数字,,,(1≤,,,≤10^9)输出:最少的秒数。Examplesinput5263output2题目解析:a、b、c之间没有关系,可以先排序,使得a=d的时候,ans=max(0,
- Codeforces Round 938 (Div. 3)
沫刃起
codeforces算法c++数据结构
A.YogurtSale#include#defineendl'\n'#defineintlonglongusingnamespacestd;intn,a,b;voidsolve(){cin>>n>>a>>b;if(2*a>t;while(t--){solve();}return0;}B.ProgressiveSquare#include#defineendl'\n'#defineintlongl
- 2023ICPC济南站训练补题
farawaytravelerchy
ACM-ICPC训练补题算法python
title:2023ICPC济南站VP补题记录(第48届)date:2024-01-1812:16:23mathjax:truetags:XCPCcategories:Algorithm文章目录2023ICPC济南站训练补题注:暂时更新vp时ac的4道题,其余题目之后持续更新[Problem-D-LargestDigit](https://codeforces.com/gym/104901/pro
- cf973Div3E
Colinnian
codeforces
https://codeforces.com/contest/2008/problem/Eusingll=longlong;voidsolve(){intn;std::cin>>n;std::strings;std::cin>>s;intans=n;//_____________________________//_____________________________//首先将奇数位置和偶数位
- Codeforces Round 969 (Div. 2 ABCDE题) 视频讲解
阿史大杯茶
Codeforces算法c++数据结构
A.Dora’sSetProblemStatementDorahasasetssscontainingintegers.Inthebeginning,shewillputallintegersin[l,r][l,r][l,r]intothesetsss.Thatis,anintegerxxxisinitiallycontainedinthesetifandonlyifl≤x≤rl\leqx\leq
- CF C. Candy Store
Jiu-yuan
算法
原题链接:Problem-C-Codeforces题意:多测,先给出n代表n种糖果,每种糖果分别给出数量和单价,可以将糖果平均分成若干袋,每一袋的的价格是一袋糖果数量×单价,对于每一种糖果都求出一袋的价格,对于每种糖果都需要用标签贴出一袋的价格,但是如果相邻的糖果价格相同,那么就可以用一个标签来代表价格,问最少使用几个标签。思路:如果一段糖果价格是一样的,那么设置价格为cost。因为每一袋糖果的价
- Codeforces Round 969 (Div. 2):A - Dora‘s Set题解C++,给自己陷入死胡同了,果然真理总是简洁朴素优美
醒了不起的盖茨比Z
c++算法leetcode动态规划c语言图论笔记
先说答案,有需要的大家看看:#includeusingnamespacestd;#defineendl'\n'intmain(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);intt,l,r;cin>>t;while(t--){cin>>l>>r;intab=r-l+1;//这一行数字的长度if((ab%4==3)&&r%2!=0)//奇数结尾会有
- 关于求数组中两部分是否相等问题可以考虑前缀和的思路
shadowcase
算法c++
当之后你不记得标题由何而来时,请回顾codeforcesround918(div4)的E题/*这道题的核心就是题干中等式的转化,然后利用前缀和。还要注意flag[0]=1不能漏,不然就都是yes了*/#includeusingnamespacestd;#definelllonglongconstintmaxn=2e5;constintmod=1e6+7;intmain(){ios::sync_wi
- codeforces round 748 题解 A~D2
刘心奶黄包qaq
算法算法c++
文章目录A.Elections题目大意思路AC代码B.MakeitDivisibleby25题目大意思路AC代码C.SaveMoreMice题目大意思路AC代码D1.AllareSame题目大意思路AC代码D2.HalfofSame题目大意思路AC代码A.ElectionsA.Elections题目大意有三个候选人,每个候选人都有一个初始票数,问每个候选人至少增加多少票才能绝对被选上。思路判断其中
- Codeforces Round 963 (Div. 2)
lskkkkkkkkkkkk
题解dp动态规划思维模拟数论
CodeforcesRound963(Div.2)A.QuestionMarks题意有一场考试一共4∗n4*n4∗n道题目,其中答案为A,B,C,D的题目各nnn道,现在你有一份考试的结果,由字母A,B,C,D组成,请问最多得到多少分。思路每种选项最多答对n道题目,我们统计每个选项的出现次数,和n取较小值,将结果加起来即可。代码#includeusingnamespacestd;#defineIO
- Codeforces Round 935 (Div. 3)
lskkkkkkkkkkkk
算法数据结构c++
题目链接A.SettingupCamp题意有一些屋子,每个屋子最多容纳三个人,有三种人,内向人必须一个人一个屋,外向人必须三个人同时一个屋子,综合人随意(一个两个三个都可)现在有aaa个内向人,bbb个外向人,ccc个综合人。问最少需要多少个屋子才能满足所有人的要求,如果无论如何都不能满足那么就输出-1思路我们很容易发现,对于内向人,不会导致输出-1.因为给他们一人一个屋子即可。对于综合人同样不会
- Codeforces Round 936 (Div. 2)
lskkkkkkkkkkkk
c++算法数据结构
CodeforcesRound936(Div.2)题目链接A.MedianofanArray题意给出一个数组aaa,每次操作可以让其中一个数增加一。问最少需要几次操作能改变中位数的值。长度为n的数组a的中位数表示为,令b是a排完序后的数组,那么b⌈n2⌉b_{\lceil\frac{n}{2}\rceil}b⌈2n⌉即为a的中位数。思路假设中位数为mmm,那么我们就需要让最终的中位数变为m+1m+
- CF 967 D. Longest Max Min Subsequence
Jiu-yuan
算法数据结构
原题链接:Problem-D-Codeforces题意:多测,每次给出长度为n的数组,要求找出没有重复元素的,最长的子序列,如果不止一个最长子序列,那么就选择字典序最小的,比较字典序的时候,如果这个元素的下标是奇数,那么就变成负数比较。思路:线段树+贪心,观察题意可知,最终的子序列肯定是正负相间的,那么对于奇数位置,这个数越大越好,对于偶数位置,这个数越小越好。那么就可以贪心的考虑这个问题,设置二
- [Codeforces 115E]Linear Kingdom Races
ddpx3313
c/c++
题目大意:有n块地,初始是荒地。你可以把某些荒地开垦(需要花费相应的价值\(a_i\)(正整数)),然后这些荒地就可以种田。现在有m年,每年要在l到r区间内种田,获得p(正整数)的价值(必须保证l~r都已经开荒,否则不能种田)。问最大收益。解题思路:DP。设F[i][j]表示前i块地,最后有连续的j块地已开荒的最大收益。则\(F[i+1][0]=max\{F[i][j]\}\)。不开荒,则中间断了
- Codeforces Round 917 (Div. 2)
Lanthanmum
算法
A.考虑有没有负数,偶数(把没有负数考虑进去了)就要改变一个数为0,为min,如果是奇数就不用考虑ー、_ィ│/////へ/ノ<|\\//ヽ_ノ(_/│////7|///>―r ̄ ̄`ー―_#include#include#include#include#include#include#include#include#include#include#include#include#include#de
- 【codeforces 115E】Linear Kingdom Races 题意&题解&代码(c++)
deritt
oi之路DERIT的博客专栏线段树-dp
**E.LinearKingdomRaces**timelimitpertest5secondsmemorylimitpertest256megabytesYouareacarraceorganizerandwouldliketoarrangesomeracesinLinearKingdom.LinearKingdomhasnconsecutiveroadsspanningfromlefttori
- E. Linear Kingdom Races
Lanthanmum
算法数据结构动态规划
https://codeforces.com/problemset/problem/115/E线段树优化dpO(n2)->O(nlogn)分析题意发现可以有暴力dpdp(i)是前i条路最大利润dp(i)=dp(i-1)不选第i条路dp(i)=max(dp(j)+val(j)-cost(j))选这i条路dp(i)=max(dp(i-1),max(dp(j)+val(j)-cost(j))显然右边值可
- 2024ccpc中国郑州
Pown_ShanYu
算法
题目链接:Dashboard-2024NationalInvitationalofCCPC(Zhengzhou),2024CCPCHenanProvincialCollegiateProgrammingContest-Codeforces文章目录F.优秀字符串J.排列与合数B.扫雷1A.OnceInMyLifeM.有效算法H.随机栈//Solve函数结合末尾模板F.优秀字符串题意:优秀字符串:长度
- Codeforces Round 967 (Div. 2) C题Guess The Tree
青衫酒145
算法
题目链接令1是根,我们可以一层一层的递推出去。容易知道询问a,b如果结果是c,那么c就是a,b路径上的中点。我们可以先让根1和其他n-1个点都询问一遍,如果返回值是1,那么这些点就是第二层,深度为2的点。我们发现一个c点会对应两层的深节点,比如一条链1234,如果询问13和14返回都会是2,那么我们就让2和34分别连一条边,表示3和4是可能和2直接连边的。然后因为第二层我们已经推出来有哪些点了,再
- Codeforces Round 938 (Div. 3)A-C,E-H
青衫酒145
c语言算法c++
题目链接A.YogurtSale贪心的选两个物品价格少的,若总个数为奇数再加是单个价格代码:#include#definelllonglongusingnamespacestd;voidsolve(){intn,a,b;cin>>n>>a>>b;intr=0;if(n&1){if(b>t;while(t--){solve();}return0;}B.ProgressiveSquare因为c,d大于
- Codeforces gym102423 - J One of Each(贪心 + 栈)
Happig丶
#
传送门题目大意给出nnn个数,仅包含[1,k][1,k][1,k]中的数,且至少含有kkk个不同的数。找到一个长度为kkk的子序列是kkk的一个排列且字典序最小。解题思路这个题算是比较难想的贪心了,而且要用栈维护。一开始用尺取发现维护不了,贪心的话自己又陷入了如下几个误区:如果从后向前贪心,显然是可以的,但是对于已经选过的数,无法得知前缀中待选的数是否能全部出现,即使bitsetbitsetbit
- CF 966 Div3 F. Color Rows and Columns
Jiu-yuan
算法
原题链接:Problem-F-Codeforces题意:多测,每组测试数据给出n和k,n代表有n个长方形,k代表需要的到k分,每个长方形都有宽和高,每次可以填涂一个格子,如果填满一列或者一行就可以获得一分,问达到k分最少需要填涂多少格子。赛时思路:背包dp+随机化,按照背包dp的思路来想,就是选择了某个长方形,如果填满这个长方形分数也不能到达k,那么就直接填满,如果大于等于k那么就用最小代价来填满
- Codeforces Round 966 (Div. 3) 前四题python题解
CodeNerd影
python开发语言
A.PrimaryTasktimelimitpertest1secondmemorylimitpertest256megabytesDmitrywrotedowntintegersontheboard,andthatisgood.Heissurethathelostanimportantintegernamongthem,andthatisbad.Theintegernnhadtheform10^
- Codeforces Round 933 (Div. 3) (A~E)
叶域
算法竞赛算法codeforcesc++
CodeforcesRound933(Div.3)(A~E)目录:ABCDEA题:RudolfandtheTicket标签:暴力枚举(bruteforce)数学(math)排序算法(sortings)双指针算法(twopointers)题目大意给一个长度为n的数组b,和一个长度为m的数组c,还有一个整数k。从b,c中各选一个数,问有多少种选法使这两个数小于等于k思路前缀和快速得出在b数组中小于等于
- Codeforces Round 927 (Div. 3)(A~E)
叶域
算法竞赛c++codeforces算法
CodeforcesRound927(Div.3)(A~E)目录:ABCDEA题:ThornsandCoins标签:动态规划(dp)贪心(greedy)实现问题,编程技巧,模拟(implementation)题目大意由n个连续单元组成的路径,每个单元可以是空的,含有荆棘,或者含有一枚硬币,在一次移动中,你可以沿着路径移动一个或两个单元,前提是目标单元不含有荆棘(并且属于路径)如果你移动到含有硬币的
- 解线性方程组
qiuwanchi
package gaodai.matrix;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
Scanner scanner = new Sc
- 在mysql内部存储代码
annan211
性能mysql存储过程触发器
在mysql内部存储代码
在mysql内部存储代码,既有优点也有缺点,而且有人倡导有人反对。
先看优点:
1 她在服务器内部执行,离数据最近,另外在服务器上执行还可以节省带宽和网络延迟。
2 这是一种代码重用。可以方便的统一业务规则,保证某些行为的一致性,所以也可以提供一定的安全性。
3 可以简化代码的维护和版本更新。
4 可以帮助提升安全,比如提供更细
- Android使用Asynchronous Http Client完成登录保存cookie的问题
hotsunshine
android
Asynchronous Http Client是android中非常好的异步请求工具
除了异步之外还有很多封装比如json的处理,cookie的处理
引用
Persistent Cookie Storage with PersistentCookieStore
This library also includes a PersistentCookieStore whi
- java面试题
Array_06
java面试
java面试题
第一,谈谈final, finally, finalize的区别。
final-修饰符(关键字)如果一个类被声明为final,意味着它不能再派生出新的子类,不能作为父类被继承。因此一个类不能既被声明为 abstract的,又被声明为final的。将变量或方法声明为final,可以保证它们在使用中不被改变。被声明为final的变量必须在声明时给定初值,而在以后的引用中只能
- 网站加速
oloz
网站加速
前序:本人菜鸟,此文研究总结来源于互联网上的资料,大牛请勿喷!本人虚心学习,多指教.
1、减小网页体积的大小,尽量采用div+css模式,尽量避免复杂的页面结构,能简约就简约。
2、采用Gzip对网页进行压缩;
GZIP最早由Jean-loup Gailly和Mark Adler创建,用于UNⅨ系统的文件压缩。我们在Linux中经常会用到后缀为.gz
- 正确书写单例模式
随意而生
java 设计模式 单例
单例模式算是设计模式中最容易理解,也是最容易手写代码的模式了吧。但是其中的坑却不少,所以也常作为面试题来考。本文主要对几种单例写法的整理,并分析其优缺点。很多都是一些老生常谈的问题,但如果你不知道如何创建一个线程安全的单例,不知道什么是双检锁,那这篇文章可能会帮助到你。
懒汉式,线程不安全
当被问到要实现一个单例模式时,很多人的第一反应是写出如下的代码,包括教科书上也是这样
- 单例模式
香水浓
java
懒汉 调用getInstance方法时实例化
public class Singleton {
private static Singleton instance;
private Singleton() {}
public static synchronized Singleton getInstance() {
if(null == ins
- 安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
AdyZhang
apachehttp server
安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
每次到这一步都很小心防它的端口冲突问题,结果,特意留出来的80端口就是不能用,烦。
解决方法确保几处:
1、停止IIS启动
2、把端口80改成其它 (譬如90,800,,,什么数字都好)
3、防火墙(关掉试试)
在运行处输入 cmd 回车,转到apa
- 如何在android 文件选择器中选择多个图片或者视频?
aijuans
android
我的android app有这样的需求,在进行照片和视频上传的时候,需要一次性的从照片/视频库选择多条进行上传
但是android原生态的sdk中,只能一个一个的进行选择和上传。
我想知道是否有其他的android上传库可以解决这个问题,提供一个多选的功能,可以使checkbox之类的,一次选择多个 处理方法
官方的图片选择器(但是不支持所有版本的androi,只支持API Level
- mysql中查询生日提醒的日期相关的sql
baalwolf
mysql
SELECT sysid,user_name,birthday,listid,userhead_50,CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')),CURDATE(), dayofyear( CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')))-dayofyear(
- MongoDB索引文件破坏后导致查询错误的问题
BigBird2012
mongodb
问题描述:
MongoDB在非正常情况下关闭时,可能会导致索引文件破坏,造成数据在更新时没有反映到索引上。
解决方案:
使用脚本,重建MongoDB所有表的索引。
var names = db.getCollectionNames();
for( var i in names ){
var name = names[i];
print(name);
- Javascript Promise
bijian1013
JavaScriptPromise
Parse JavaScript SDK现在提供了支持大多数异步方法的兼容jquery的Promises模式,那么这意味着什么呢,读完下文你就了解了。
一.认识Promises
“Promises”代表着在javascript程序里下一个伟大的范式,但是理解他们为什么如此伟大不是件简
- [Zookeeper学习笔记九]Zookeeper源代码分析之Zookeeper构造过程
bit1129
zookeeper
Zookeeper重载了几个构造函数,其中构造者可以提供参数最多,可定制性最多的构造函数是
public ZooKeeper(String connectString, int sessionTimeout, Watcher watcher, long sessionId, byte[] sessionPasswd, boolea
- 【Java命令三】jstack
bit1129
jstack
jstack是用于获得当前运行的Java程序所有的线程的运行情况(thread dump),不同于jmap用于获得memory dump
[hadoop@hadoop sbin]$ jstack
Usage:
jstack [-l] <pid>
(to connect to running process)
jstack -F
- jboss 5.1启停脚本 动静分离部署
ronin47
以前启动jboss,往各种xml配置文件,现只要运行一句脚本即可。start nohup sh /**/run.sh -c servicename -b ip -g clustername -u broatcast jboss.messaging.ServerPeerID=int -Djboss.service.binding.set=p
- UI之如何打磨设计能力?
brotherlamp
UIui教程ui自学ui资料ui视频
在越来越拥挤的初创企业世界里,视觉设计的重要性往往可以与杀手级用户体验比肩。在许多情况下,尤其对于 Web 初创企业而言,这两者都是不可或缺的。前不久我们在《右脑革命:别学编程了,学艺术吧》中也曾发出过重视设计的呼吁。如何才能提高初创企业的设计能力呢?以下是 9 位创始人的体会。
1.找到自己的方式
如果你是设计师,要想提高技能可以去设计博客和展示好设计的网站如D-lists或
- 三色旗算法
bylijinnan
java算法
import java.util.Arrays;
/**
问题:
假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,
您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳
子上进行这个动作,而且一次只能调换两个旗子。
网上的解法大多类似:
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来
- 警告:No configuration found for the specified action: \'s
chiangfai
configuration
1.index.jsp页面form标签未指定namespace属性。
<!--index.jsp代码-->
<%@taglib prefix="s" uri="/struts-tags"%>
...
<s:form action="submit" method="post"&g
- redis -- hash_max_zipmap_entries设置过大有问题
chenchao051
redishash
使用redis时为了使用hash追求更高的内存使用率,我们一般都用hash结构,并且有时候会把hash_max_zipmap_entries这个值设置的很大,很多资料也推荐设置到1000,默认设置为了512,但是这里有个坑
#define ZIPMAP_BIGLEN 254
#define ZIPMAP_END 255
/* Return th
- select into outfile access deny问题
daizj
mysqltxt导出数据到文件
本文转自:http://hatemysql.com/2010/06/29/select-into-outfile-access-deny%E9%97%AE%E9%A2%98/
为应用建立了rnd的帐号,专门为他们查询线上数据库用的,当然,只有他们上了生产网络以后才能连上数据库,安全方面我们还是很注意的,呵呵。
授权的语句如下:
grant select on armory.* to rn
- phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('This example should only be run from a Web Brows
- 美国电影超短200句
dcj3sjt126com
电影
1. I see. 我明白了。2. I quit! 我不干了!3. Let go! 放手!4. Me too. 我也是。5. My god! 天哪!6. No way! 不行!7. Come on. 来吧(赶快)8. Hold on. 等一等。9. I agree。 我同意。10. Not bad. 还不错。11. Not yet. 还没。12. See you. 再见。13. Shut up!
- Java访问远程服务
dyy_gusi
httpclientwebservicegetpost
随着webService的崛起,我们开始中会越来越多的使用到访问远程webService服务。当然对于不同的webService框架一般都有自己的client包供使用,但是如果使用webService框架自己的client包,那么必然需要在自己的代码中引入它的包,如果同时调运了多个不同框架的webService,那么就需要同时引入多个不同的clien
- Maven的settings.xml配置
geeksun
settings.xml
settings.xml是Maven的配置文件,下面解释一下其中的配置含义:
settings.xml存在于两个地方:
1.安装的地方:$M2_HOME/conf/settings.xml
2.用户的目录:${user.home}/.m2/settings.xml
前者又被叫做全局配置,后者被称为用户配置。如果两者都存在,它们的内容将被合并,并且用户范围的settings.xml优先。
- ubuntu的init与系统服务设置
hongtoushizi
ubuntu
转载自:
http://iysm.net/?p=178 init
Init是位于/sbin/init的一个程序,它是在linux下,在系统启动过程中,初始化所有的设备驱动程序和数据结构等之后,由内核启动的一个用户级程序,并由此init程序进而完成系统的启动过程。
ubuntu与传统的linux略有不同,使用upstart完成系统的启动,但表面上仍维持init程序的形式。
运行
- 跟我学Nginx+Lua开发目录贴
jinnianshilongnian
nginxlua
使用Nginx+Lua开发近一年的时间,学习和实践了一些Nginx+Lua开发的架构,为了让更多人使用Nginx+Lua架构开发,利用春节期间总结了一份基本的学习教程,希望对大家有用。也欢迎谈探讨学习一些经验。
目录
第一章 安装Nginx+Lua开发环境
第二章 Nginx+Lua开发入门
第三章 Redis/SSDB+Twemproxy安装与使用
第四章 L
- php位运算符注意事项
home198979
位运算PHP&
$a = $b = $c = 0;
$a & $b = 1;
$b | $c = 1
问a,b,c最终为多少?
当看到这题时,我犯了一个低级错误,误 以为位运算符会改变变量的值。所以得出结果是1 1 0
但是位运算符是不会改变变量的值的,例如:
$a=1;$b=2;
$a&$b;
这样a,b的值不会有任何改变
- Linux shell数组建立和使用技巧
pda158
linux
1.数组定义 [chengmo@centos5 ~]$ a=(1 2 3 4 5) [chengmo@centos5 ~]$ echo $a 1 一对括号表示是数组,数组元素用“空格”符号分割开。
2.数组读取与赋值 得到长度: [chengmo@centos5 ~]$ echo ${#a[@]} 5 用${#数组名[@或
- hotspot源码(JDK7)
ol_beta
javaHotSpotjvm
源码结构图,方便理解:
├─agent Serviceab
- Oracle基本事务和ForAll执行批量DML练习
vipbooks
oraclesql
基本事务的使用:
从账户一的余额中转100到账户二的余额中去,如果账户二不存在或账户一中的余额不足100则整笔交易回滚
select * from account;
-- 创建一张账户表
create table account(
-- 账户ID
id number(3) not null,
-- 账户名称
nam
 题解
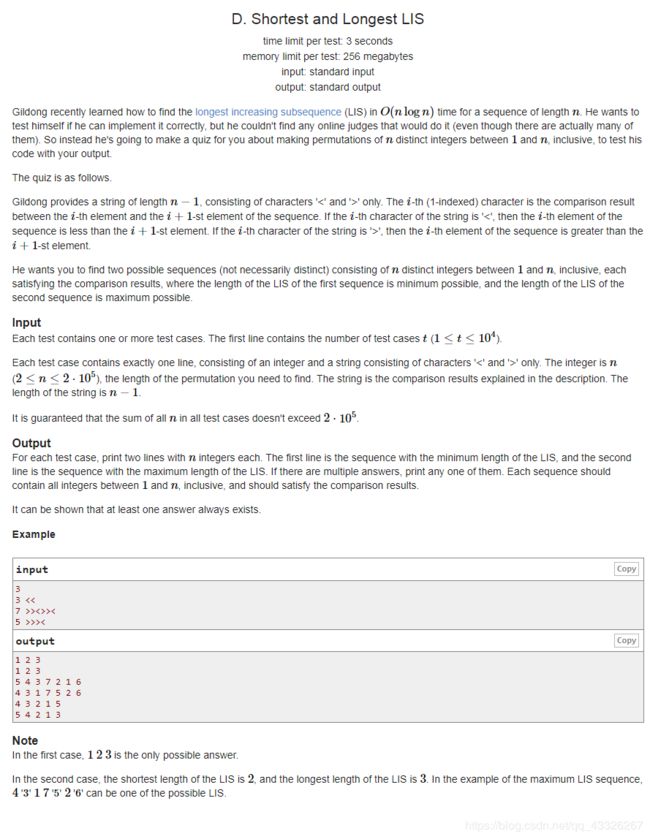
题解![]() ,反之小于。第一位我们默认为1。那么为了便于构造,我们肯定是尽量卡边缘,换言之,每一段连续的0和连续的1代表的数就是连续的。就比如序列1111,我们就可以放1234,序列0000,我们就放4321。所以,如果是构造最长,我们就让所有的1可以连起来。如果是最短,就不让每一段1连起来就可以了。
,反之小于。第一位我们默认为1。那么为了便于构造,我们肯定是尽量卡边缘,换言之,每一段连续的0和连续的1代表的数就是连续的。就比如序列1111,我们就可以放1234,序列0000,我们就放4321。所以,如果是构造最长,我们就让所有的1可以连起来。如果是最短,就不让每一段1连起来就可以了。