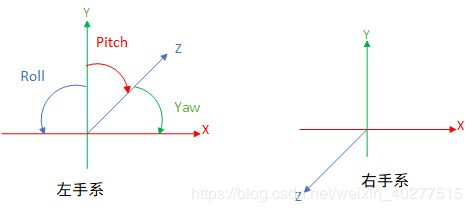
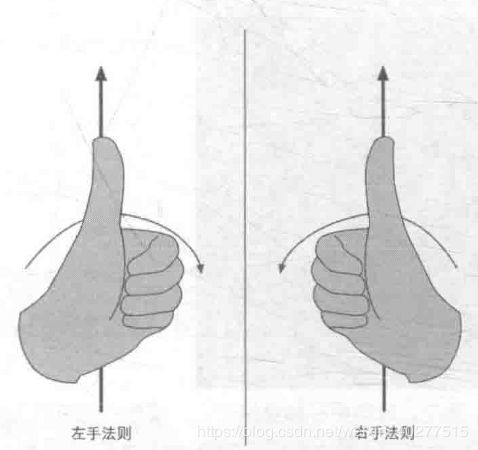
左右手坐标系的转换
文章目录
- 左手系与右手系的旋转正方向
- 点的转换
- 旋转的转换
- 旋转矩阵
- 四元数
- 结论
- X轴取反
- Y轴取反
- Z轴取反
本文描述了左右手坐标系的数据转换过程,其中包括点,平移,旋转(旋转矩阵,四元数)。以不同手系中点的转换出发,详细推导了旋转矩阵以及四元数的转换过程,并且在文末的结论中给出了三种情况下(X轴取反,Y轴取反,Z轴取反)的平移(点)和旋转的转换(旋转矩阵,四元数)。
参考:左右手坐标系的数据转换
左手系与右手系的旋转正方向
- 判断方法:大拇指指向旋转轴正方向,剩余四个手指弯曲方向为旋转正方向。可以看出左手系中旋转正方向是顺时针,右手系中旋转正方向是逆时针
点的转换
点在左右手系中的转换最简单,只需要将某一个轴分量取反。以Z轴取反为例,右手系中的点Pr(x,y,z)在左手系中转换为点Pl(x,y,-z),用矩阵表示为:
P l = [ x y − z ] = [ 1 0 0 0 1 0 0 0 − 1 ] [ x y z ] = S T P r P_l=\begin{bmatrix} x\\y\\-z\\\end{bmatrix} = \begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix} \begin{bmatrix}x \\y\\z\end{bmatrix}=S_TP_r Pl=⎣⎡xy−z⎦⎤=⎣⎡10001000−1⎦⎤⎣⎡xyz⎦⎤=STPr
点的转换矩阵为:
S T = [ 1 0 0 0 1 0 0 0 − 1 ] S_T= \begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix} ST=⎣⎡10001000−1⎦⎤
旋转的转换
旋转矩阵
假设一个右手系中的旋转矩阵为:
R r = [ r 00 r 01 r 02 r 10 r 11 r 12 r 20 r 21 r 22 ] R_r=\begin{bmatrix}r_{00}&r_{01}&r_{02}\\r_{10}&r_{11}&r_{12}\\r_{20}&r_{21}&r_{22}\end{bmatrix} Rr=⎣⎡r00r10r20r01r11r21r02r12r22⎦⎤
输入一个点Pr(x,y,z)经过该矩阵变换后输出点Pr’(x’,y’,z’):
P r ′ = [ x ′ y ′ z ′ ] = [ r 00 r 01 r 02 r 10 r 11 r 12 r 20 r 21 r 22 ] [ x y z ] = R r P r P'_r= \begin{bmatrix} x'\\y'\\z'\end{bmatrix}=\begin{bmatrix}r_{00}&r_{01}&r_{02}\\r_{10}&r_{11}&r_{12}\\r_{20}&r_{21}&r_{22}\end{bmatrix} \begin{bmatrix} x\\y\\z\end{bmatrix}=R_rP_r Pr′=⎣⎡x′y′z′⎦⎤=⎣⎡r00r10r20r01r11r21r02r12r22⎦⎤⎣⎡xyz⎦⎤=RrPr
在左手系中,输入和输出的Z轴分量都取反,于是在左手系中的变换为 P l = ( x , y , − z ) → ( x ′ , y ′ , − z ′ ) = P l ′ P_l=(x,y,-z)\rightarrow (x',y',-z')=P_l' Pl=(x,y,−z)→(x′,y′,−z′)=Pl′
又
P l ′ = S T P r ′ = S T R r P r = S T R r S T P l P_l'=S_TP_r'=S_TR_rP_r=S_TR_rS_TP_l Pl′=STPr′=STRrPr=STRrSTPl
因此,在左手系中的旋转矩阵变为:
R l = S T R r S T R_l=S_TR_rS_T Rl=STRrST
可以理解为在左手系中将该旋转拆分为三步:
- 将左手系中的点变换到右手系中
- 根据右手系中的旋转矩阵进行旋转
- 将旋转后的点变换到左手系中
将点转换矩阵带入计算:
R l = [ 1 0 0 0 1 0 0 0 − 1 ] [ r 00 r 01 r 02 r 10 r 11 r 12 r 20 r 21 r 22 ] [ 1 0 0 0 1 0 0 0 − 1 ] = [ r 00 r 01 − r 02 r 10 r 11 − r 12 − r 20 − r 21 r 22 ] R_l=\begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix} \begin{bmatrix}r_{00}&r_{01}&r_{02}\\r_{10}&r_{11}&r_{12}\\r_{20}&r_{21}&r_{22}\end{bmatrix} \begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix} =\begin{bmatrix}r_{00}&r_{01}&-r_{02}\\r_{10}&r_{11}&-r_{12}\\-r_{20}&-r_{21}&r_{22}\end{bmatrix} Rl=⎣⎡10001000−1⎦⎤⎣⎡r00r10r20r01r11r21r02r12r22⎦⎤⎣⎡10001000−1⎦⎤=⎣⎡r00r10−r20r01r11−r21−r02−r12r22⎦⎤
四元数
由旋转矩阵转四元数的转换公式可得:
q 0 l = 1 + t r ( R l ) 2 = q 0 q 1 l = − r 12 − ( − r 21 ) 4 q 0 = − r 12 − r 21 4 q 0 = − q 1 q 2 l = − r 20 − ( − r 02 ) 4 q 0 = − r 20 − r 02 4 q 0 = − q 2 q 3 l = r 01 − r 10 4 q 0 = q 3 q_{0l}=\frac{\sqrt{1+tr(R_l)}}{2}=q_0\\ q_{1l}=\frac{-r_{12}-(-r_{21})}{4q_0}=-\frac{r_{12}-r_{21}}{4q_0}=-q_1\\ q_{2l}=\frac{-r_{20}-(-r_{02})}{4q_0}=-\frac{r_{20}-r_{02}}{4q_0}=-q_2\\ q_{3l}=\frac{r_{01}-r_{10}}{4q_0}=q_3 q0l=21+tr(Rl)=q0q1l=4q0−r12−(−r21)=−4q0r12−r21=−q1q2l=4q0−r20−(−r02)=−4q0r20−r02=−q2q3l=4q0r01−r10=q3
结论
X轴取反
点转换矩阵:
S T = [ − 1 0 0 0 1 0 0 0 1 ] S_T= \begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\end{bmatrix} ST=⎣⎡−100010001⎦⎤
旋转矩阵:
[ r 00 − r 01 − r 02 − r 10 r 11 r 12 − r 20 r 21 r 22 ] \begin{bmatrix}r_{00}&-r_{01}&-r_{02}\\-r_{10}&r_{11}&r_{12}\\-r_{20}&r_{21}&r_{22}\end{bmatrix} \\ ⎣⎡r00−r10−r20−r01r11r21−r02r12r22⎦⎤
四元数:
q 0 l = q 0 q 1 l = q 1 q 2 l = − q 2 q 3 l = − q 3 q_{0l}=q_0\\ q_{1l}=q_1\\ q_{2l}=-q_2\\ q_{3l}=-q_3 q0l=q0q1l=q1q2l=−q2q3l=−q3
Y轴取反
点转换矩阵:
S T = [ 1 0 0 0 − 1 0 0 0 1 ] S_T= \begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\end{bmatrix} ST=⎣⎡1000−10001⎦⎤
旋转矩阵:
[ r 00 − r 01 r 02 − r 10 r 11 − r 12 r 20 − r 21 r 22 ] \begin{bmatrix}r_{00}&-r_{01}&r_{02}\\-r_{10}&r_{11}&-r_{12}\\r_{20}&-r_{21}&r_{22}\end{bmatrix} \\ ⎣⎡r00−r10r20−r01r11−r21r02−r12r22⎦⎤
四元数:
q 0 l = q 0 q 1 l = − q 1 q 2 l = q 2 q 3 l = − q 3 q_{0l}=q_0\\ q_{1l}=-q_1\\ q_{2l}=q_2\\ q_{3l}=-q_3 q0l=q0q1l=−q1q2l=q2q3l=−q3
Z轴取反
点转换矩阵:
S T = [ 1 0 0 0 1 0 0 0 − 1 ] S_T= \begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix} ST=⎣⎡10001000−1⎦⎤
旋转矩阵:
[ r 00 r 01 − r 02 r 10 r 11 − r 12 − r 20 − r 21 r 22 ] \begin{bmatrix}r_{00}&r_{01}&-r_{02}\\r_{10}&r_{11}&-r_{12}\\-r_{20}&-r_{21}&r_{22}\end{bmatrix} \\ ⎣⎡r00r10−r20r01r11−r21−r02−r12r22⎦⎤
四元数:
q 0 l = q 0 q 1 l = − q 1 q 2 l = − q 2 q 3 l = q 3 q_{0l}=q_0\\ q_{1l}=-q_1\\ q_{2l}=-q_2\\ q_{3l}=q_3 q0l=q0q1l=−q1q2l=−q2q3l=q3