Kalman滤波
来自：https://www.cnblogs.com/ycwang16/p/5999034.html
虽然Kalman滤波器已经被广泛使用，也有很多的教程，但我们在Bayes滤波器的框架上，来深入理解Kalman滤波器的设计，对理解采用Gaussian模型来近似状态分布的多高斯滤波器(Guassian Multi-Hyperthesis-Filter)等都有帮助。
一. 背景知识回顾 \textbf{一. 背景知识回顾} 一. 背景知识回顾
1.1 Bayes滤波
首先回顾一下Bayes滤波. Bayes滤波分为两步：1.状态预测 、 2.状态更新
-
状态预测，基于状态转移模型：
b e l ‾ ( x t ) = ∫ p ( x t ∣ u t , x t − 1 ) b e l ( x t − 1 ) d x t − 1 \overline {bel} ({x_t}) = \int {p({x_t}|{u_t},{x_{t - 1}})} \;bel({x_{t - 1}})\;d{x_{t - 1}} bel(xt)=∫p(xt∣ut,xt−1)bel(xt−1)dxt−1 -
状态更新，基于新的观测
b e l ( x t ) = η p ( z t ∣ x t ) b e l ‾ ( x t ) bel({x_t}) = \;\eta \,p({z_t}|{x_t})\,\overline {bel} ({x_t}) bel(xt)=ηp(zt∣xt)bel(xt)
我们可以看到，我们的目的是计算 x t x_t xt的后验概率，如果 b e l ( x t ) bel(x_t) bel(xt)是任意分布，我们需要在 x t x_t xt的所有可能取值点上，计算该取值的概率，这在计算上是难于实现的。这一计算问题可以有多种方法来近似，比如利用采样的方法，就是后面要讲的粒子滤波和无迹Kalman滤波。
这节要说的近似方法是，当假设 b e l ( x t ) bel(x_t) bel(xt)服从Gauss分布，那么我们只需要分布的均值和方差就可以完全描述 b e l ( x t ) bel(x_t) bel(xt),而无需在 x t x_t xt的每个可能取值点上进行概率计算。这也是用高斯分布来近似 b e l ( x t ) bel(x_t) bel(xt)的好处，因为我们在每一个时刻，只需要计算均值 μ t \mu_t μt和方差 Σ t \Sigma_t Σt这两个数值，就可以对 b e l ( x t ) bel(x_t) bel(xt)完全描述，所以我们就可以推导出这两个数值的递推公式，从而在每个时刻由这两个数值的递推公式完全获得状态估计，这就是The Kalman Filter的基本思想。
1.2 正态分布(Guassian Distribution)
然后我们再回顾一下正态分布的基础知识。正态分布是一种特殊的概率分布，分布的形态完全由二阶矩决定。一元高斯分布表述如下：
p ( x ) ∼ N ( μ , σ 2 ) : p ( x ) = 1 2 π σ e − 1 2 ( x − μ ) 2 σ 2 \begin{array}{l} p(x)\sim N(\mu ,{\sigma ^2}):\\ p(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{1}{2}\frac{{{{(x - \mu )}^2}}}{{{\sigma ^2}}}}} \end{array} p(x)∼N(μ,σ2):p(x)=2πσ1e−21σ2(x−μ)2
其中，一阶矩为均值 μ \mu μ表示期望值，二阶矩为方差 σ \sigma σ 表示分布的不确定程度。
多元高斯分布的表达式为： p ( x ) ∼ N ( μ , Σ ) : p ( x ) = 1 ( 2 π ) d / 2 ∣ Σ ∣ 1 / 2 e − 1 2 ( x − μ ) t Σ − 1 ( x − μ ) \begin{array}{l} p({\bf{x}})\sim {\rm N}({\bf{\mu }},{\bf{\Sigma }}):\\ p({\bf{x}}) = \frac{1}{{{{(2\pi )}^{d/2}}{{\left| {\bf{\Sigma }} \right|}^{1/2}}}}{e^{ - \frac{1}{2}{{({\bf{x}} - {\bf{\mu }})}^t}{{\bf{\Sigma }}^{ - 1}}({\bf{x}} - {\bf{\mu }})}} \end{array} p(x)∼N(μ,Σ):p(x)=(2π)d/2∣Σ∣1/21e−21(x−μ)tΣ−1(x−μ)
一阶矩为均值 μ \mu μ表示期望值，二阶矩为方差 Σ \Sigma Σ 表示分布的不确定程度。
1.3 正态分布的特点
在线性变换下，一旦高斯，代代高斯。
首先，高斯变量线性变换后，仍为高斯分布，均值和方差如下：
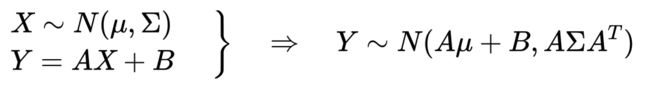然后，两个高斯变量线性组合，仍为高斯分布，均值和方差如下：
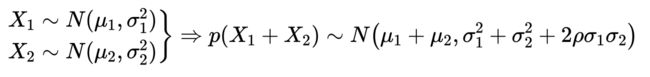最后，两个相互独立的高斯变量的乘积，仍然为高斯分布，均值和方差如下：
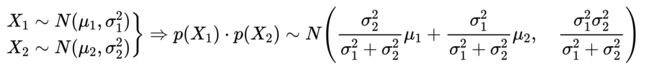
正因为高斯分布有这些特点，所以，在Bayes滤波公式中的随机变量的加法、乘法，可以用解析的公式计算均值和方差，这使得Bayes滤波的整个计算过程非常简便，即Kalman滤波器的迭代过程。
二. Kalman滤波 \textbf{二. Kalman滤波} 二. Kalman滤波
2.1 Kalman滤波的模型假设
Kalman滤波所解决的问题，是对一个动态变化的系统的状态跟踪的问题，基本的模型假设包括：1）系统的状态方程是线性的；2）观测方程是线性的；3）过程噪声符合零均值高斯分布；4）观测噪声符合零均值高斯分布；从而，一直在线性变化的空间中操作高斯分布，状态的概率密度符合高斯分布。
- 状态方程
x t = A t x t − 1 + B t u t + ε t {x_t} = {A_t}{x_{t - 1}} + {B_t}{u_t} + {\varepsilon _t} xt=Atxt−1+Btut+εt
- 观测方程
z t = H t x t + δ t {z_t} = {H_t}{x_t} + {\delta _t} zt=Htxt+δt
其中过程噪声 ϵ t \epsilon_t ϵt假设符合零均值高斯分布；观测噪声 δ t \delta_t δt假设符合零均值高斯分布。对于上述模型，我们可以用如下参数描述整个问题：
2.2 Kalman滤波器的模型
-
x t x_t xt, n n n维向量，表示t时刻观测状态的均值.
-
P t P_t Pt, n × n n\times n n×n方差矩阵，表示 t t t时刻被观测的 n n n个状态的方差.
-
u t u_t ut, l l l维向量，表示 t t t时刻的输入
-
z t z_t zt, m m m维向量，表示 t t t时刻的观测
-
A t A_t At, n × n n\times n n×n矩阵，表示状态从 t − 1 t-1 t−1到 t t t在没有输入影响时转移方式
-
B t B_t Bt, n × n n\times n n×n矩阵 表示 u t u_t ut如何影响 x t x_t xt
-
H t H_t Ht, m × n m\times n m×n表示状态 x t x_t xt如何被转换为观测 z t z_t zt
-
R t R_t Rt, n × n n\times n n×n矩阵，表示过程噪声 ϵ t \epsilon_t ϵt 的方差矩阵
-
Q t Q_t Qt, m × m m\times m m×m矩阵,表示观测噪声 ϵ t \epsilon_t ϵt 的方差矩阵
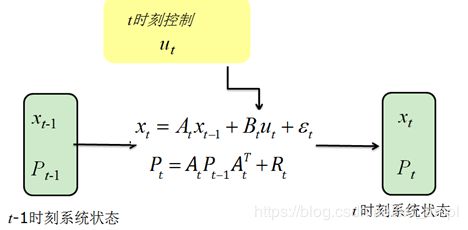
上图给出了在没有观测，仅有输入 u t u_t ut时，状态变量的均值和方差从 t − 1 t−1 t−1到 t t t的转移方式，可见均值和方差的计算，完全是基于高斯分布的线性变化的方法来算的。
上图给出了Kalman滤波所解决的问题，即在获得 t t t时刻的输入和观测的情况下，如何更新 x t x_t xt的均值和方差的问题。当然 u t u_t ut和 z t z_t zt也并不是每一个时刻都需要同时获得，就像贝叶斯滤波一样，可以在获得 u t u_t ut时就做一次状态预测，在获得 z t z_t zt时做一次状态更新.
2.3 Kalman滤波算法
Kalman滤波整体算法如下:
⋅ \boldsymbol{\cdot} ⋅ 第一行基于转移矩阵和控制输入，预测 t t t时刻的状态.
⋅ \boldsymbol{\cdot} ⋅ 第二行是预测方差矩阵.
⋅ \boldsymbol{\cdot} ⋅ 第三行计算Kalman增益， K t \boldsymbol{K_t} Kt
⋅ \boldsymbol{\cdot} ⋅ 第四行基于观测的新息进行状态更新
⋅ \boldsymbol{\cdot} ⋅ 第五行计算更新状态的方差矩阵。
可以看到算法的所有的精妙之处都在于第三行和第四行。我们可以这样来理解：
-
( H t P ‾ t H t T + Q t ) ({H_t}{\overline P _t}H_t^T + {Q_t}) (HtPtHtT+Qt)代表对状态进行观测时，观测的不确定程度，它与Kalman增益 K t \boldsymbol{K_t} Kt成反比，表示观测的可能噪声越大的时候，Kalman增益 K t \boldsymbol{K_t} Kt越小。
-
再看第四行， x t x_t xt的更新是在 x ˉ t \bar{x}_t xˉt上加一个 K t \boldsymbol{K_t} Kt乘以 ( z t − H t x ‾ t ) ({z_t} - {H_t}{\overline x _t}) (zt−Htxt). ( z t − H t x ‾ t ) ({z_t} - {H_t}{\overline x _t}) (zt−Htxt)代表的是预测的值与观测之间的差异，这个差异当预测和观测都比较接近于真实值时比较小。当观测不准，或者预测不准时都会比较大。而前面的乘子 K t \boldsymbol{K_t} Kt是在观测噪声大的时候比较小，所以整个 K t ( z t − H t x ‾ t ) \boldsymbol{K_t}({z_t} - {H_t}{\overline x _t}) Kt(zt−Htxt)这个修正量，表示利用观测对预测结果的修正量。
⋅ \qquad \cdot ⋅ 当观测噪声比较小，预测误差比较大时修正幅度比较大
⋅ \qquad \cdot ⋅ 当观测噪声比较小预测误差比较小的时候，或者观测噪声比较大的时候，修正误差的幅度也比较小，从而起到了一种平滑的作用。
- 利用较准确的观测修正预测误差，不准确的观测修正量也较小，所以在误差较大的时候能快速修正，而在误差较小时能逐渐收敛。
2.4 Kalman滤波算法的推导 \textbf{2.4 Kalman滤波算法的推导} 2.4 Kalman滤波算法的推导
这里我们用Bayes公式，给出Kalman Filter是如何导出的。
- 系统的初始状态是：
b e l ( x 0 ) = N ( μ 0 , P 0 ) bel({x_0}) = N\left( {{\mu _0},{P_0}} \right) bel(x0)=N(μ0,P0)
- 预测过程的推导
状态转移模型是线性函数
x t = A t x t − 1 + B t u t + ε t {x_t} = {A_t}{x_{t - 1}} + {B_t}{u_t} + {\varepsilon _t} xt=Atxt−1+Btut+εt
所以，由 x t − 1 x_{t−1} xt−1到 x t x_t xt状态转移的条件概率为:
p ( x t ∣ u t , x t − 1 ) = N ( A t x t − 1 + B t u t , R t ) p({x_t}|{u_t},{x_{t - 1}}) = N\left( {{A_t}{x_{t - 1}} + {B_t}{u_t},{R_t}} \right) p(xt∣ut,xt−1)=N(Atxt−1+Btut,Rt)
回顾Bayes公式，计算预测状态的分布，需要考虑所有可能的 x t − 1 x_{t−1} xt−1
b e l ‾ ( x t ) = ∫ p ( x t ∣ u t , x t − 1 ) b e l ( x t − 1 ) d x t − 1 \overline {bel} ({x_t}) = \int {p({x_t}|{u_t},{x_{t - 1}})} {\rm{ }}bel({x_{t - 1}})\;d{x_{t - 1}} bel(xt)=∫p(xt∣ut,xt−1)bel(xt−1)dxt−1
这正是计算两个高斯分布的卷积的过程，参考文献[2]：
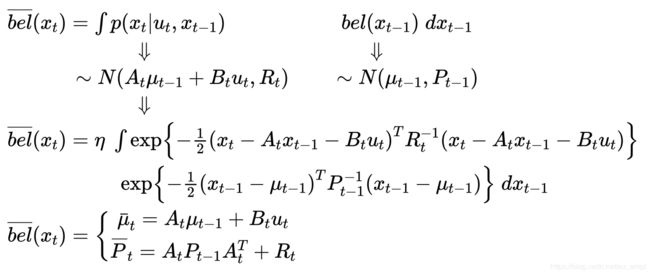
所以Kalman滤波器的预测过程，正是基于两个高斯分布的卷积计算得到的解析表达式。
3. 观测更新过程的推导
观测方程也是线性方程，并且噪声是高斯噪声
z t = H t x t + δ t {z_t} = {H_t}{x_t} + {\delta _t} zt=Htxt+δt
所以 p ( z t ∣ x t ) p(z_t|x_t) p(zt∣xt)的条件概率是高斯分布的线性变换计算：
p ( z t ∣ x t ) = N ( H t x t , Q t ) p({z_t}|{x_t}) = N\left( {{H_t}{x_t},{Q_t}} \right) p(zt∣xt)=N(Htxt,Qt)
再考虑贝叶斯公式的状态更新步骤
b e l ( x t ) = η p ( z t ∣ x t ) b e l ‾ ( x t ) bel({x_t}) = \,\quad \eta \quad \,p({z_t}|{x_t})\overline {bel} ({x_t}) bel(xt)=ηp(zt∣xt)bel(xt)
这正是两个高斯分布的乘积的问题，参考文献[2]
b e l ( x t ) = η p ( z t ∣ x t ) b e l ‾ ( x t ) ⇓ ⇓ ∼ N ( z t ; H t x t , Q t ) ∼ N ( x t ; μ ‾ t , P ‾ t ) ⇓ b e l ( x t ) = η exp { − 1 2 ( z t − H t x t ) T Q t − 1 ( z t − H t x t ) } exp { − 1 2 ( x t − μ ˉ t ) T P ˉ t − 1 ( x t − μ ˉ t ) } \begin{array}{l} bel({x_t}) = \,\quad \eta \quad \,p({z_t}|{x_t})\quad \quad \quad \quad \quad \quad \overline {bel} ({x_t})\\ \quad \quad \quad \quad \quad \quad \quad \quad \Downarrow \quad \quad \quad \quad \quad \quad \quad \quad \Downarrow \\ \quad \quad \quad \quad \quad \sim N\left( {{z_t};{H_t}{x_t},{Q_t}} \right)\quad \quad \sim N\left( {{x_t};{{\overline \mu }_t},{{\overline P }_t}} \right)\\ \quad \quad \quad \quad \quad \quad \quad \quad \Downarrow \\ bel({x_t}) = \eta \;\exp \left\{ { - \frac{1}{2}{{({z_t} - {H_t}{x_t})}^T}Q_t^{ - 1}({z_t} - {H_t}{x_t})} \right\}\exp \left\{ { - \frac{1}{2}{{({x_t} - {{\bar \mu }_t})}^T}\bar P_t^{ - 1}({x_t} - {{\bar \mu }_t})} \right\}\\ \end{array} bel(xt)=ηp(zt∣xt)bel(xt)⇓⇓∼N(zt;Htxt,Qt)∼N(xt;μt,Pt)⇓bel(xt)=ηexp{−21(zt−Htxt)TQt−1(zt−Htxt)}exp{−21(xt−μˉt)TPˉt−1(xt−μˉt)}
所以，基于求高斯变量乘积的分布的方法，可以导出结果仍然是高斯分布，用它的二阶矩表示:
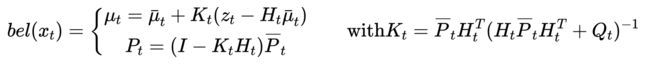
所以状态更新中的Kalman增益，均值和方差的更新公式，都是这样导出的。
Kalman滤波的算法特点
-
Kalman滤波计算快速，计算复杂度为 O ( m 2.376 + n 2 ) O(m^{2.376}+n^2) O(m2.376+n2)，其中 m m m是观测的维数； n n n是状态的个数。
-
对于线性系统，零均值高斯噪声的系统，Kalman是理论上无偏的，最优滤波器。
-
Kalman滤波在实际使用中，要注意参数 R R R和 Q Q Q的调节，这两者实际上是相对的，表示更相信观测还是更相信预测。具体使用时， R R R可以根据过程噪声的幅度决定，然后 Q Q Q可以相对 R R R来给定。当更相信观测时，把 Q Q Q调小，不相信观测时，把 Q Q Q调大。
-
Q Q Q越大，表示越不相信观测，这是系统状态越容易收敛，对观测的变化响应越慢。 Q Q Q越小，表示越相信观测，这时对观测的变化响应快，但是越不容易收敛。
https://www.cnblogs.com/ycwang16/p/5999034.html
参考文献
[1]. Sebastian Thrun, Wolfram Burgard, Dieter Fox, Probabilistic Robotics, 2002, The MIT Press.
[2]. P.A. Bromiley, Products and Convolutions of Gaussian Probability Density Functions, University of Manchester