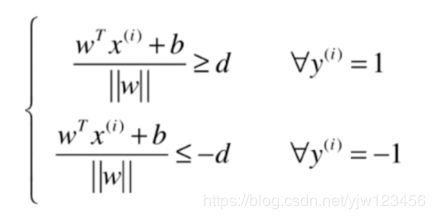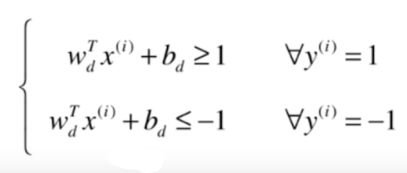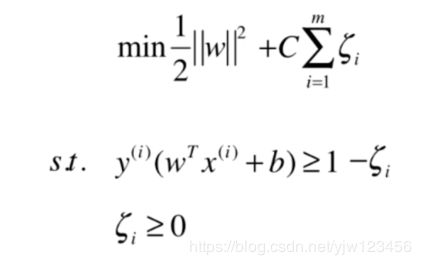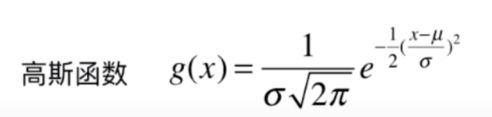机器学习入门——支持向量机图文介绍(附代码)

支持向量机(Support Vector Machine)

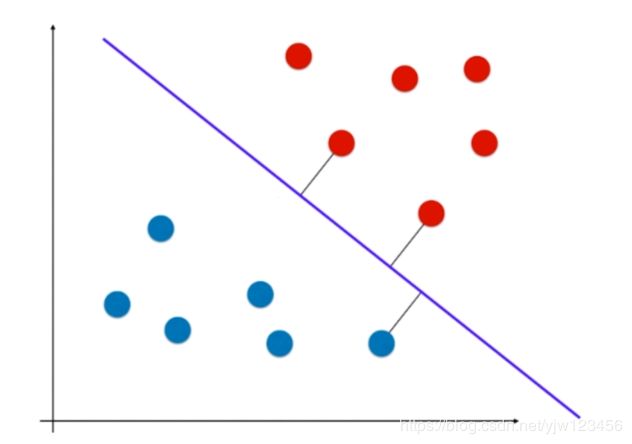
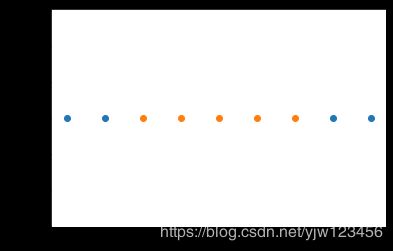
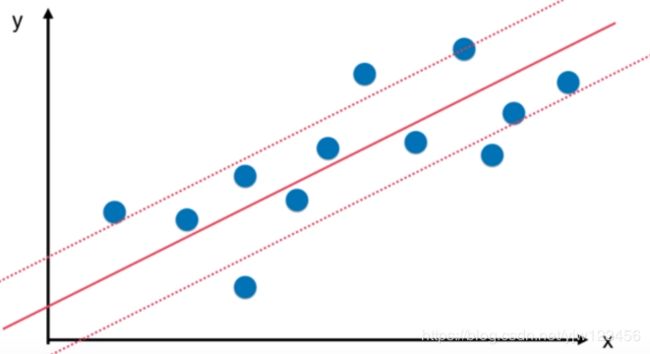
在感知机中，我们介绍过，假设存在这样的两类点，我们可以学得一条决策边界将它们分开，比如是条这样的直线：

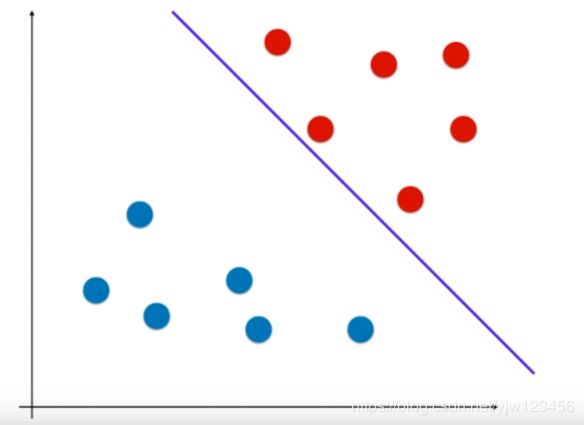
但是得到的决策边界不唯一，根据选择训练集数据的顺序可以得到不同的决策边界：

但是这两条决策边界的泛化能力都不好，为什么这么说呢，因为这两条线都离某个类别的点太近了，很可能测试集中未知的点会被错误的分类。

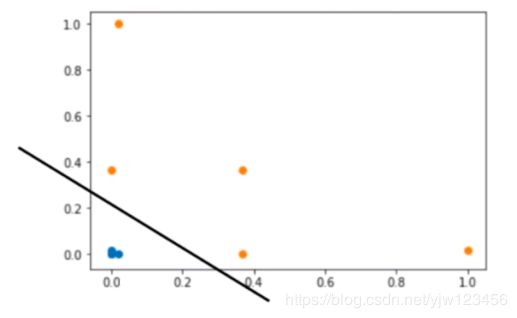
那么什么样的决策边界才是最好的呢？

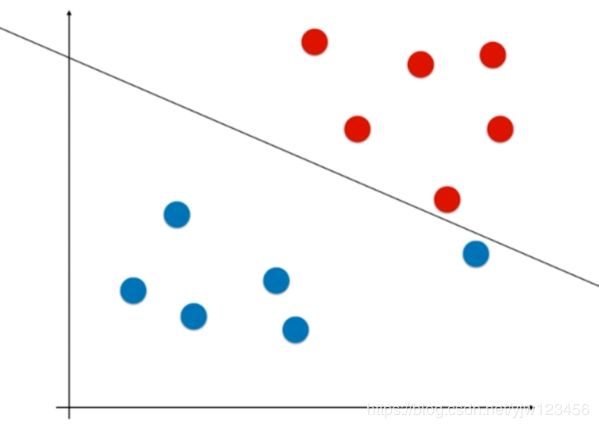
这就是一条比较好的决策边界，它离红色样本点和蓝色样本点一样远。在两个类别中，离决策边界最近的那些点都尽可能的远。红色样本有两个点，蓝色样本有一个点，这三个点到决策边界的距离是所有样本点中最近的，且距离是相等的。

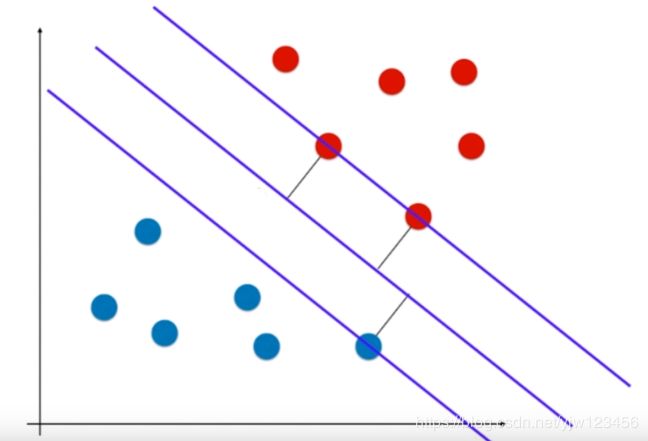
这三个点定义出了两条和决策边界平行的线。这两条平行线之间没有任何的样本点。这就是支持向量机的思想。

SVM尝试找到中间那条最优的决策边界，这个决策边界距离两个类别最近的样本最远。

这些最近的样本点就是支持向量，这也是为什么叫支持向量机。

这两条平行线离决策边界的距离相等，记为$d$，margin就是$2d$。

SVM就是要最大化margin。

上面我们讲的都是假设样本点是线性可分的情况，就是存在一条直线(平面)能将这些样本划分。这样的算法通常又称为Hard Margin SVM。

但是实际情况中，很多数据是线性不可分的，这时SVM可以通过改进得到Soft Margin SVM。

最大化margin

那如何通过数学的方式表达这个margin呢。上面我们说过$margin=2d$，SVM要最大化margin，也就是要最大化d。所以我们需要找到d的表达式。

这个d就是点到直线的距离，在感知机中我们已经介绍过了。

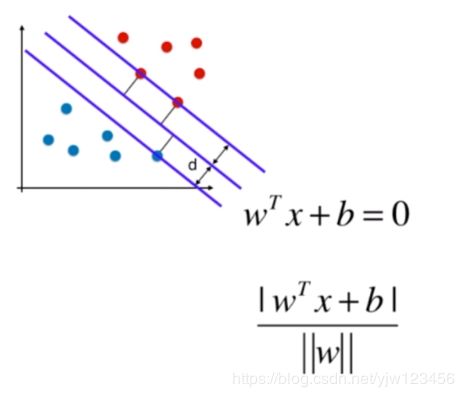
假设我们要求的决策边界由$w^{T}x+b=0$表示，距离公式如上。

对于这两类样本点，和感知机一样，分别用$+1,-1$表示。

也就有：

对于属于类别$+1$的样本点，都有距离大于等于$d$；对于$-1$的点，都有距离小于等于$-d$。

我们可以对上式进行一个变形，把两边都除以$d$：

$||w||$是一个标量,$d$也是一个标量，我们可想象把$w^T$每个元素和$b$都除以分母$||w||d$这个标量，我们用新的字母来表示除以之后的结果：

此时与决策边界平行的这两条直线分别就是$w_d^{T}x+b_d=1$和$w_d^{T}x+b_d=-1$。

对于中间决策边界，我们也可以除以$||w||d$这个标量，它的右侧等于$0$，为了简便，此时我们去掉下标$d$，还是用$w,b$来表示它们。

现在的式子如上。右边是个分段函数，我们可以用一个式子描述：

$$y^i(w^T{x}^i+b)\ge 1$$

可以代入$y^i$去验证看看。

此时对于任意支持向量$x$，我们最大化d，就是最大化下面这个式子：

$$max\frac{w^{T}x+b}{||w||}$$

而对于支持向量，它的结果要么等于$1$，要么等于$-1$。上面取绝对值后就是$1$，上式可以简写成：

$$max\frac{1}{||w||}=min||w||$$

为了方便求导，通常写成
$$min\frac{1}{2}||w|{|}^2$$

整个支持向量机的最优化问题就变成了，在条件

$$y^i(w^T{x}^i+b)\ge 1$$
的情况下，最优化

$$min\frac{1}{2}||w|{|}^2$$

这是有条件的最优化问题，具体的求解比较复杂。这里就不展开了。

Soft Margin SVM

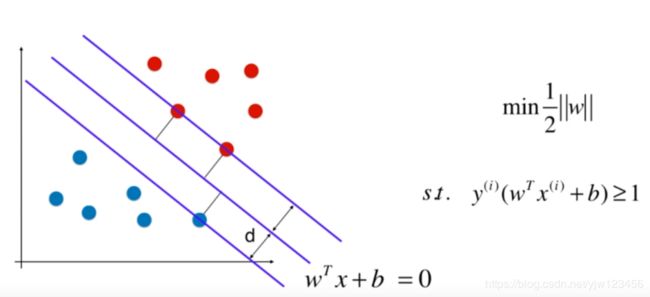
在Hard Margin SVM 中本质就是求解一个这样有条件最小化问题。但是如果某类的样本点分布比较奇怪，如

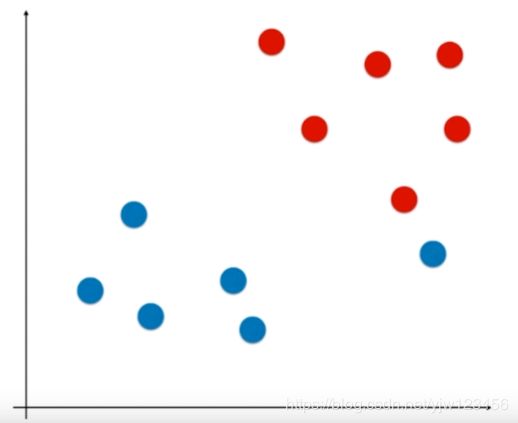
此时Hard Margin SVM要做的是找出一条直线分开这两种类别：

虽然它正确的分开了蓝色样本和红色样本，但是离红色样本太近的。对于大多数的蓝色样本点都集中在左下角位置，只有一个outlier在右边的位置。很可能这个outlier是错误的点。哪怕它是正确的点，它也不能代表一般的点。

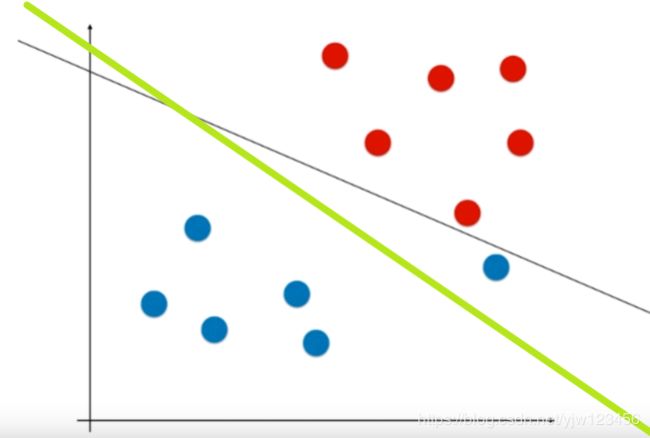
很可能绿色这个决策边界才是比较好的，虽然它错误的分类了outlier的点，但是可能在真实情况下表现的更好。也就是泛化能力更强。

所以我们的SVM算法要有一定的容错能力，在一些情况下可以把某些点进行错误的分类，尽量保证泛化能力较高。

这种SVM就叫Soft Margin SVM，我们上面说Hard Margin SVM的条件是

$$y^i(w^T{x}^i+b)\ge 1$$

它的意思是对于margin区域里，必须是任何数据点都没有的。

现在我们宽松个条件，这个宽松量记为${\zeta }_i$

把条件宽松为：

$$y^i(w^T{x}^i+b)\ge 1-{\zeta }_i$$

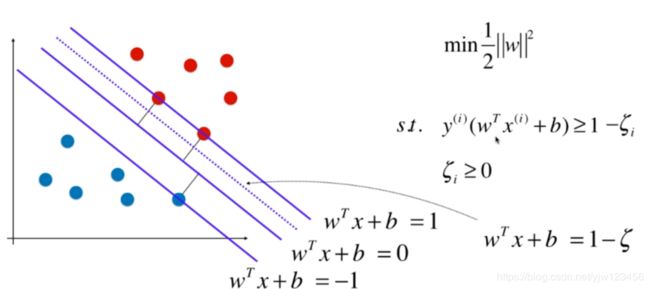
也就是说，宽松条件后，样本点可以出现在虚线与平行于决策边界的直线之间。上面是$w^{T}x+b=1$与$w^{T}x+b=1-\zeta$之间。

同时，这个$\zeta \ge 0$

为了防止$\zeta$设的过大，我们需要对最小化的式子做一个限制，增加一个正则项：

$$min\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\zeta }_i$$

这就是Soft Margin SVM完整的式子：

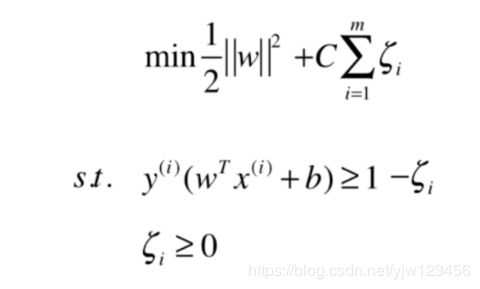
这里增加了一个超参数$C$来控制正则项的重要程度。$C$越小容错空间越大。

我们通过代码来理解一下：

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()

X = iris.data
y = iris.target

X = X [y<2,:2] #只取y<2的类别，也就是0 1 并且只取前两个特征
y = y[y<2] # 只取y<2的类别

# 分别画出类别0和1的点
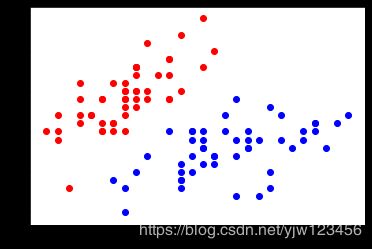
plt.scatter(X[y==0,0],X[y==0,1],color='red') 
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

# 标准化
standardScaler = StandardScaler()

standardScaler.fit(X) #计算训练数据的均值和方差
X_standard = standardScaler.transform(X) #再用scaler中的均值和方差来转换X，使X标准化

svc = LinearSVC(C=1e9) #线性SVM分类器
svc.fit(X_standard,y) # 训练svm

下图是未经标准化的原始数据点分布

训练好了之后，我们绘制这个决策边界:

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


# 绘制决策边界
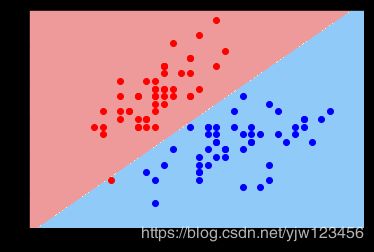
plot_decision_boundary(svc,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

上面说了$C$是控制正则项的重要程度，这里我们再次实例化一个svc，并传入一个较小的$C$。

svc2 = LinearSVC(C=0.01)
svc2.fit(X_standard,y)
plot_decision_boundary(svc2,axis=[-3,3,-3,3]) # x,y轴都在-3到3之间
# 绘制原始数据
plt.scatter(X_standard[y==0,0],X_standard[y==0,1],color='red') 
plt.scatter(X_standard[y==1,0],X_standard[y==1,1],color='blue')
plt.show()

可以很明显的看到和第一个决策边界的不同，在这个决策边界汇总，有一个红点是分类错误的。

$C$越小容错空间越大。

我们可以通过svc.coef_来获取学习到的权重系数,svc.intercept_获取偏差。

使用多项式特征和核函数

接下来我们看下如何处理非线性的数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

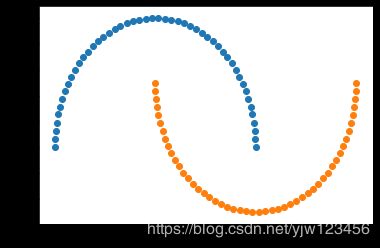
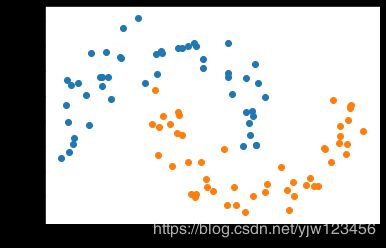
X, y = datasets.make_moons() #使用生成的数据
print(X.shape) # (100,2)
print(y.shape) # (100,)

接下来绘制下生成的数据

plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

生成的数据像月亮，这就是它函数名称的由来。但是生成的数据集太规范了，我们增加一些噪声点。

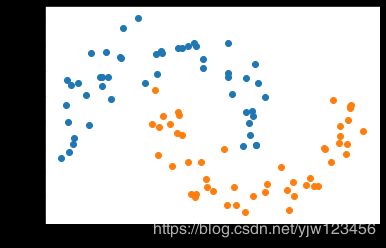
X, y = datasets.make_moons(noise=0.15,random_state=777) #随机生成噪声点，random_state是随机种子，noise是方差

plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

我们接下来通过多项式特征的SVM来对它进行分类。

from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),#生成多项式
        ("std_scaler",StandardScaler()),#标准化
        ("linearSVC",LinearSVC(C=C))#最后生成svm
    ])

这里我们引入了管道，它可以将许多算法模型串联起来，比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。

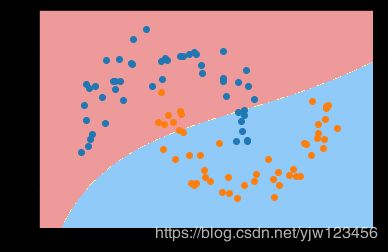
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X,y)

plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

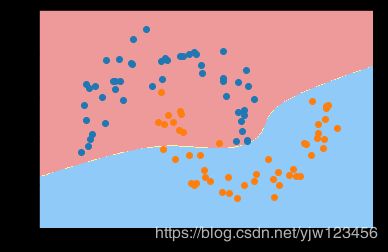
我们可以看到，生成的边界不再是线性的直线了。

我们还可以使用核技巧来对数据进行处理，使其维度提升，使原本线性不可分的数据，在高维空间变成线性可分的。再用线性SVM来进行处理。

from sklearn.svm import SVC

def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("kernelSVC",SVC(kernel="poly")) # poly代表多项式特征
    ])

poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)

plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

可以看到这种方式也生成了一个非线性的边界。

这里SVC(kernel="poly")有个参数是kernel，就是核函数。下面介绍下核函数。

核函数

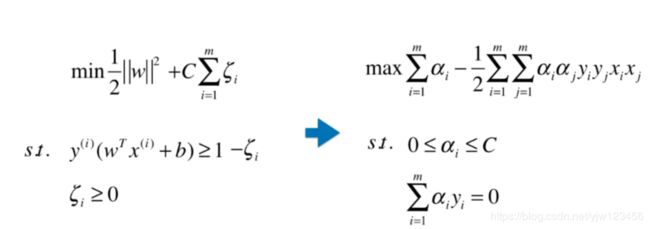
我们知道SVM的本质是求解这样一个最优化问题。

我们通过对偶形式可以将它转换一下：

上面后面的$x_i{x}_j$，我们将它们转换成多项式的特征:

最后变成要求解

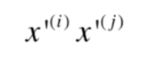
如果有这样一个函数，可以不需要分别转换$x^i,x^j$之后再相乘，而直接计算出最后的结果

那么我们的式子可以这样表示：

这个函数是存在的，它就是核函数。这也是使用核函数的技巧，所以有时你会听到核技巧这个概念。

在(二次)多项式核函数中，它的定义是这样的：

$K(x,y)=(x\cdot y+1{)}^2$

这两个向量的点乘可以写成求和的形式

展开后如上。其实这个式子就可以看出若干项相乘再相加。

相当于原来的$x$变成了这样(包含了二次项)

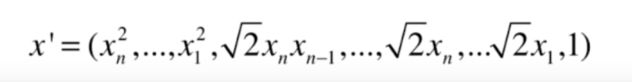
$y$也根据这个规则变成了$y^{\prime }$，这两新的向量相乘再相加，结果就是

整个过程可以不用弄的这么复杂，我们可以直接用原来的式子$K(x,y)=(x\cdot y+1{)}^2$进行计算，这就是核技巧，大大降低了计算的复杂度。

如果是多项式(大于二项)，它的式子就是这样的：

$$K(x,y)=(x\cdot y+c{)}^d$$

这个$d$就是上面程序中degree的值。这里的$c$是另外一个超参数。

我们也可以用核函数来表示原来的线性SVM，此时的核函数很简单，就是$K(x,y)=x\cdot y$。

除了多项式核函数，还有很多不同的核函数，其中最有名的就是RBF核函数(高斯核函数)。

RBF核函数

它的式子如下：

$$K(x,y)=e^{-\gamma ||x-y|{|}^2}$$

这里的$\gamma$也是超参数。

我们看下高斯函数的式子，发现高斯核函数和高斯函数很像。

高斯核函数也叫RBF核(Radia Basis Function Kernel)。

高斯核函数的本质是将每个样本点映射到一个无穷多维度的特征空间中。

核函数都是依靠升维使得原本线性不可分的数据变得线性可分。

在多项式特征中，假如原本的数据是$x$的话，我们把原来的数据都变成$x^2$，这样就变得线性可分了。

原本的数据，是一维的，它是线性不可分的，我们无法只画一条直线将它们分开。

接下来进行升维：

把它们都变成$x^2$，现在就变成了线性可分的，我们可以画一条直线来分开它们：

高斯核本质也是做这样的事情。这里为了简单，我们固定$y$为$l_1,l_2$。

它的升维式子比较复杂，我们用代码来模拟一下：

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-4,5,1)#生成测试数据
y = np.array((x >= -2 ) & (x <= 2),dtype='int')

plt.scatter(x[y==0],[0]*len(x[y==0]))# x取y=0的点, y取0，有多少个x，就有多少个y
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

接下来使用高斯核函数，看如何将一个一维的数据映射到二维的空间。

# 高斯核函数
def gaussian(x,l):
    gamma = 1.0
    return np.exp(-gamma * (x -l)**2)

l1,l2 = -1,1
X_new = np.empty((len(x),2)) #len(x) ,2
for i,data in enumerate(x):
    X_new[i,0] = gaussian(data,l1)
    X_new[i,1] = gaussian(data,l2)
    
plt.scatter(X_new[y==0,0],X_new[y==0,1])
plt.scatter(X_new[y==1,0],X_new[y==1,1])
plt.show()

对于这样的二维数据显然是线性可分的：

这里我们为了简单固定了$y$，其实实际上的核函数是下面这样的：

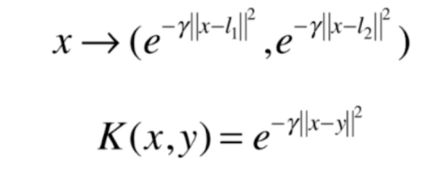
高斯核函数将$m\times n$的数据映射成了$m\times m$的数据，原本只有$n$个维度的数据，经过高斯核之后变成了$m$维度，如果$m$非常大的话，就映射成了一个非常高维的空间点。

如果我们的样本点是无穷多个的，那么它就会映射出无穷维的数据(如果向量$y$每个维度的值都不同的话)。但是通常我们的样本再多也是有限的，因此最终得到的是有限维的映射。

当我们初始的样本数据维度较高，但是样本数量不多时($m<n$)，我们可以使用高斯核来进行处理。最典型的应用领域是自然语言处理，在自然语言处理中，通常我们会构造一个非常高维的样本空间，但是我们的样本数量是不太多的。

超参数$\gamma$

在高斯函数中，$\sigma$越大，分布就越胖。

而核函数中的 $\gamma$类似于 $\frac{1}{2{\sigma }^2}$。

所以，$\gamma$越大，高斯分布越窄；$\gamma$越小，高斯分布越宽。

接下来用代码来演示下$\gamma$的取值对结果的影响。

首先是生成我们的数据:

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X,y = datasets.make_moons(noise=0.15,random_state=777)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

接下来定义一个RBF核的SVM：

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline

def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

svc = RBFKernelSVC()
svc.fit(X,y)

plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1]) 
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

这是我们设置$\gamma =1.0$时所得到的决策边界。我们调整下它的值再试下：

svc = RBFKernelSVC(100)

其他代码不变：

$\gamma$取值越大，就是高斯分布的钟形图越窄，这里相当于每个样本点都形成了钟形图。很明显这样是过拟合的。

我们再设一下$\gamma$

svc = RBFKernelSVC(10)

再调小一点:

svc = RBFKernelSVC(0.1)

此时它是欠拟合的。

因此，我们可以看出$\gamma$值相当于在调整模型的复杂度。

SVM解决回归问题

我们回归问题的本质是找到这样一条线能尽可能的拟合我们的数据点。

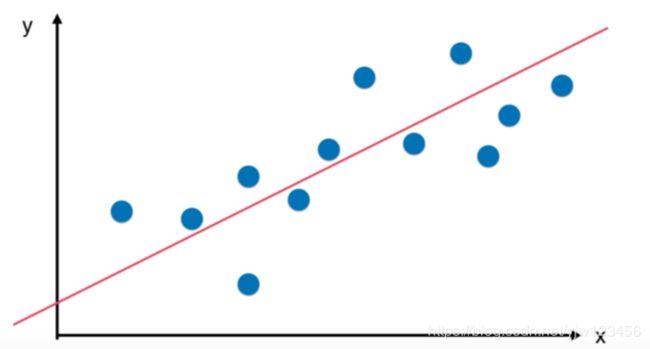
对于SVM来说，对于拟合的定义是指定margin值，期望在margin范围里包含的数据点越多越好。

此时，我们取中间的这条直线作为回归的结果。这和解决分类问题是一个相反的思路。

下面我们看下代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target

from sklearn.model_selection import train_test_split

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=777) # 把数据集拆分成训练数据和测试数据

from sklearn.svm import LinearSVR 
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler

def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('linearSVR',LinearSVR(epsilon=epsilon))
    ])

svr = StandardLinearSVR()
svr.fit(X_train,y_train)

svr.score(X_test,y_test) #0.6989278257702748

参考

1.Python3入门机器学习