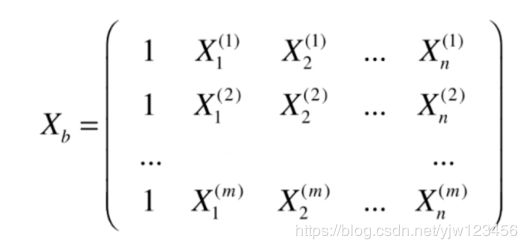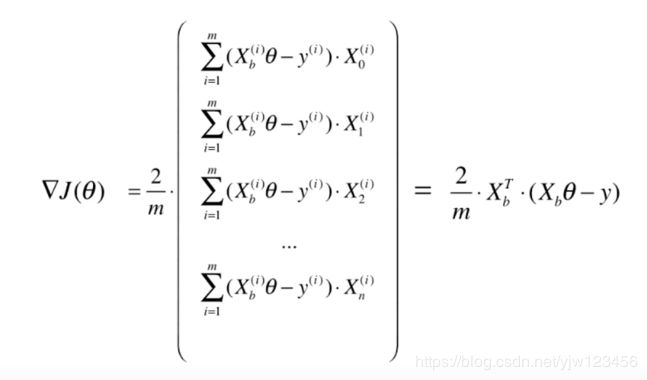机器学习入门——梯度下降算法详解
引言
本文介绍机器学习中非常重要的一个优化算法——梯度下降法。它不是一个机器学习算法,但是它是能帮助机器学习算法进行训练的算法。梯度下降法是基于搜索的最优化方法,它的作用是优化一个损失函数。
提示:本文略长,阅读前可以准备一杯咖啡放旁边。
在机器学习领域,熟练的掌握梯度法来求解目标函数的最优解是一个非常重要的事情。
梯度下降法
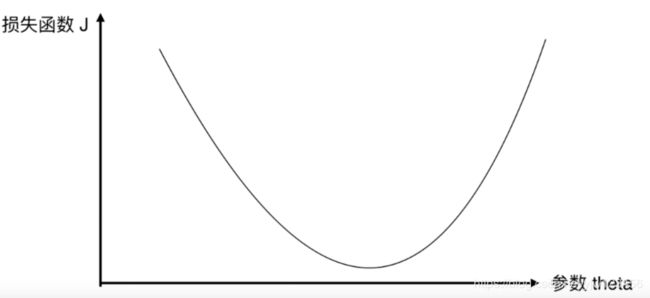
梯度下降法是用来最小化我们的损失函数的。这里我们有一个参数与损失函数值的图像。
对于我们最小化损失函数这个任务来说,相当于是在这样一个坐标系中找到使得损失函数最小的参数。同样的,这里我们假设参数只有一个,以便在二维平面中展示它。
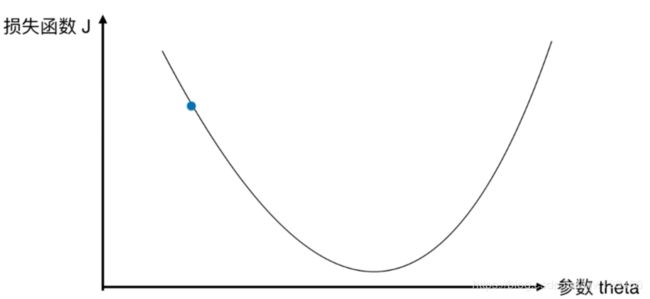
对于损失函数J来说,每取一个参数值,相应的就会有个损失J。
我们知道如果这一点,它的导数不为零,那么它肯定不在极值点上,这里我们说的导数是 d J d θ \frac{dJ}{d\theta} dθdJ。
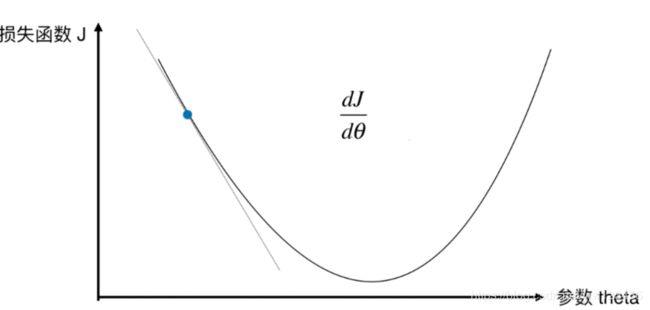
在直线方程中,导数就代表斜率;而在曲线方程中,导数代表的是该点处切线的斜率。
换一个角度来理解导数的话,代表当参数变化时,J相应的变化程度。要注意导数的正负,上图蓝点的导数为负值,当参数增加时,J是减少的。
这就说明导数可以代码J增加的方向。因为该点处的导数是负值,所以J增加的方向应该是参数减少的方向。
如果我们希望找到J的最小值,我们希望这个点能对应J减少的方向移动。所以就应该向导数的负方向移动,因此这里取负号。
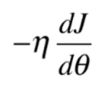
通常我们还要设置一个移动的步长,这个步长记为 η \eta η。通常 η \eta η取一个较小的值,比如取 0.1 0.1 0.1,那么这里参数就要减去 0.1 0.1 0.1乘以 d J d θ \frac{dJ}{d\theta} dθdJ。
这点我们的导数是负值,乘以一个 − 0.1 -0.1 −0.1就得到了正值,因此我们的J减少,参数会增大。
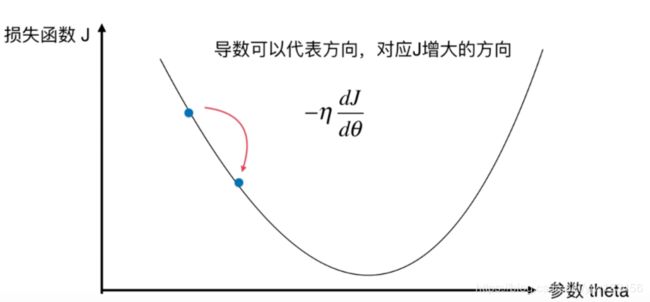
我们在新的点再求一下导数,发现该点的导数仍然是负值。那我们再尝试把参数变化(增加) − η -\eta −η乘 d J d θ \frac{dJ}{d\theta} dθdJ这么多。
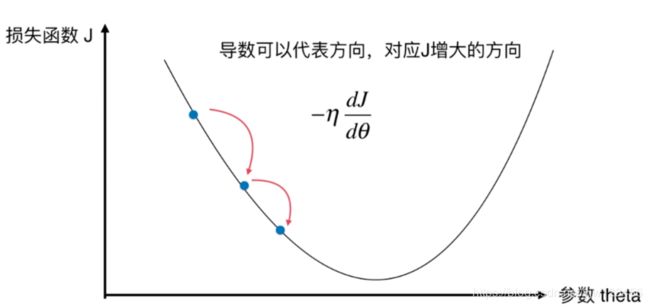
我们继续这个过程,直到导数等于零。说明我们的J处于一个极小值。从我们的图示可以看到,这个点时逐渐下降的,这也是该方法叫梯度下降法的原因。
那为什么叫梯度呢,我们这个例子中用的是一维的图像,如果我们有两个参数
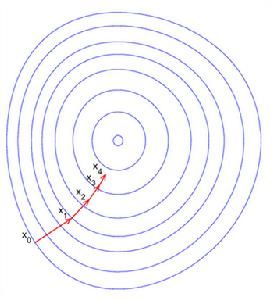
如上图,我们要在这两个参数上分别求导,最终得到的方向就是梯度。
我们回到上面的导数。此时假设我们的初始点在右边。
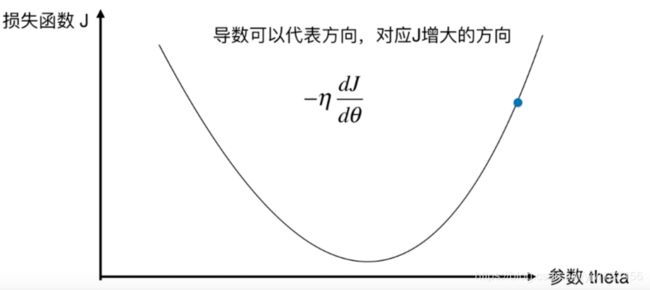
该点的导数是大于零的,我们要找到J的最小值,此时就要使得J的值变小,而导数代表的是J增大的方向,所以我们要向导数的负方向走。
所以 − η d J d θ -\eta \frac{d J}{d \theta} −ηdθdJ这个式子依然成立。
我们还是减去 η \eta η乘以 d J d θ \frac{d J}{d \theta} dθdJ,由于此时导数是大于零的,参数就会变小。该点因此会向左边移动。
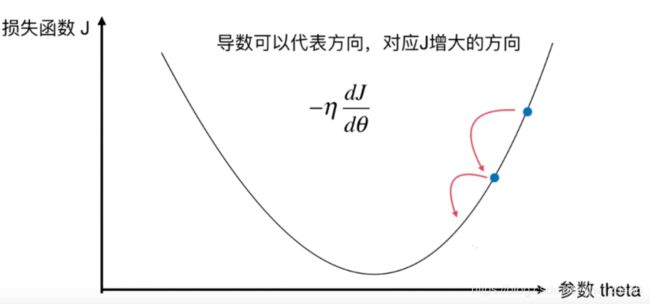
来到新点后,重复同样的过程还是继续向左移动。
如果把损失函数的图像想象成一个碗,我们在碗壁上放一个球,不管怎么放,这个球都会滚动碗底。
梯度下降法就是模拟球滚落的过程,直到球滚到碗底,我们就说找到了损失函数J最小值的位置。
滚动的速度由 η \eta η来决定,我们通常称这个 η \eta η为学习率(learning rate)。
学习率的取值是很重要的;它是梯度下降法的一个超参数;学习率的取值影响获得最优解的速度;如果取值不合适(取值过大),甚至无法得到最优解。
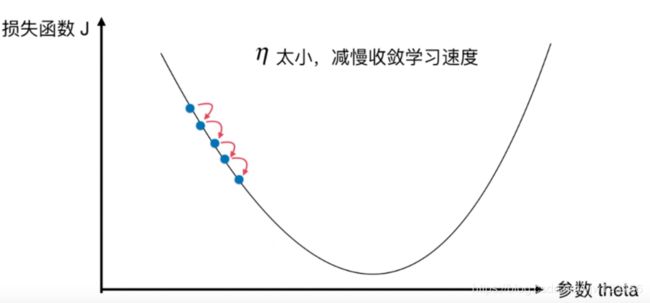
如果 η \eta η太小,每次移动的步长就小,滚动的就慢,这会影响我们整个算法得到最终的最优解的速度,也就是收敛的速度。
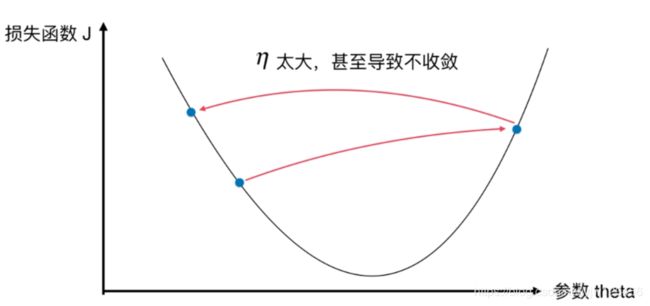
反之,如果 η \eta η过大,移动的步长太大,很有直接几步就蹦出去了,导致无法收敛。
但是,并不是所有的函数都有唯一的极值点。
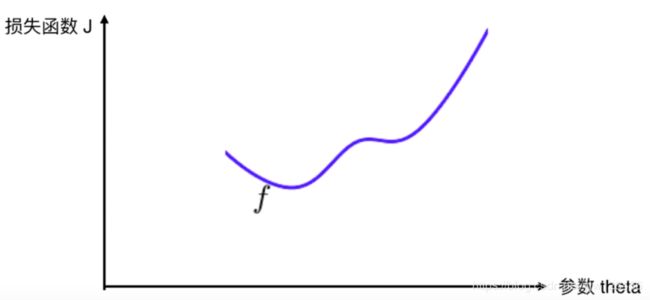
比如这个函数,它有两个极小值,左边的是最小值,右边的是局部最小值。这两个极小值的位置导数都为零。
假如我们使用梯度下降法来求解这个损失函数J,如果从最右边的红点出发
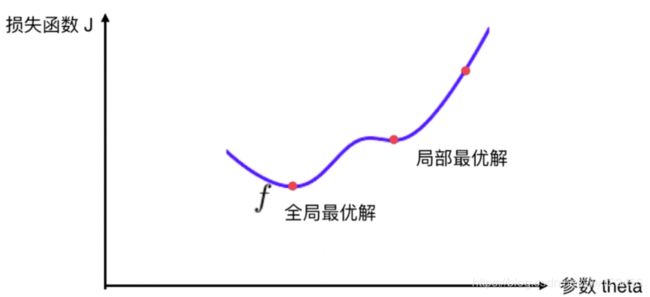
很有可能找到的最优解是局部最优解,而不是全局最优解。
对于这个问题的解决方案通常是:
- 随机初始化点多次运行
如果我们初始点的位置是在左边,那么就很有可能找到全局最优解。
所以梯度下降法的初始点也是一个超参数。

不过在线性回归中我们的损失函数是具有唯一最优解的。
可视化梯度下降法
首先画出我们自定义的损失函数图像:
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1,6,141) #从-1到6之间等间距生成140个点
plot_y = (plot_x - 2.5)**2 - 1 #我们的损失函数
plt.plot(plot_x,plot_y)
plt.show()
我们要先计算梯度函数对参数 x x x的导数,就是求
d ( ( x − 2.5 ) 2 − 1 ) d x = 2 ( x − 2.5 ) \frac{d((x - 2.5)^2 - 1)}{d x} = 2(x -2.5) dxd((x−2.5)2−1)=2(x−2.5)
def dJ(theta):
return 2 * (theta - 2.5)
然后表示一下损失函数:
def J(theta):
return (theta - 2.5)**2 - 1
下面就能开始模拟梯度下降法了。
我们初始化 θ = 0 \theta = 0 θ=0
theta = 0.0
eta = 0.1 #初始化学习率
epsilon = 1e-8 #10⁻⁸ ,表示一个很小的数,如果损失函数的差值小于这个很小的数,我们就认为导数等于零了
while True: #先用死循环,后面会改成迭代次数
gradient = dJ(theta) # 先求出梯度
last_theta = theta #保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
if abs(J(theta) - J(last_theta)) < epsilon:
break
print(theta) # 2.499891109642585
print(J(theta)) # -0.99999998814289
这里定义了一个epsilon,用来判断导数是否等于0,因为计算机无法准确判断浮点数0.00000000的相等。当这次计算出来的损失函数的值减去上次的小于epsilon,我们就认为导数是等于0的,整个梯度下降过程就可以停止了。
得到的theta=2.499891109642585,由数学知识我们知道,在 θ = 2.5 \theta = 2.5 θ=2.5处导数值为0。得到的结果也逼近这个数了(可以调小epsilon的值让结果更加逼近)。
下面重点来了,我们可视化上面这个过程,来看一下我们的学习率是如何影响梯度下降法的。
因此我们要改下代码,记录下每次求到的theta。
theta = 0.0
theta_history =[theta]
eta = 0.1 #初始化学习率
epsilon = 1e-8 #10⁻⁸ ,表示一个很小的数,如果损失函数的差值小于这个很小的数,我们就认为导数等于零了
while True: #先用死循环,后面会改成迭代次数
gradient = dJ(theta) # 先求出梯度
last_theta = theta #保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
theta_history.append(theta)
if abs(J(theta) - J(last_theta)) < epsilon:
break
plt.plot(plot_x,J(plot_x))# 绘制出损失函数的曲线
plt.plot(np.array(theta_history),J(np.array(theta_history)),'r+') #绘制theta,x轴传入theta值,y轴是对应的J(theta)
plt.show()
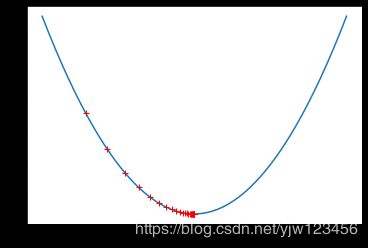
我们可以看到,梯度下降法从 θ = 0 \theta = 0 θ=0的点出发,一步一步落到损失函数最小值的位置。
并且可以看到刚开始步伐较大,因为刚开始的导数的绝对值(曲线很陡)很大,越到后面导数的绝对值(曲线平缓)越小,所以步伐就越小。
直到最后我们根据abs(J(theta) - J(last_theta)) < epsilon判断出最后走的这一步代来我们损失函数值上的差距小于我们设定的epsilon,我们就停止整个算法。
len(theta_history)#46
从theta_history中可以看到我们只经过45(还有一个是初始值)次查找就得到了最小值。
接下来我们改变我们的学习率eta值来看看不同的效果,我们提高代码的复用率,我们把上面梯度下降的代码封装成一个函数:
def gradient_descent(initial_theta,eta,epsilon=1e-8):
theta = initial_theta
theta_history.append(theta) #theta_history成了一个全局变量
while True: #先用死循环,后面会改成迭代次数
gradient = dJ(theta) # 先求出梯度
last_theta = theta #保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
theta_history.append(theta)
if abs(J(theta) - J(last_theta)) < epsilon:
print(len(theta_history) - 1) #打印计算次数
break
def plot_theta_history():
plt.plot(plot_x,J(plot_x))# 绘制出损失函数的曲线
plt.plot(np.array(theta_history),J(np.array(theta_history)),color='red',marker='+') #绘制theta
plt.show()
下面我先将eta设定为一个较小的值:
theta_history = [] #初始化全局变量
gradient_descent(initial_theta=0.0,eta=0.01)#为了看得清楚,这里显示标明了参数
plot_theta_history()
打印出来的迭代次数是423,图像如下:
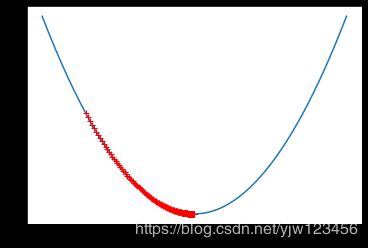
可以看到,我们的学习率变下, 步长变小,需要的迭代次数要多。从图上看图像上的点更加密集。这样会花费更多的时间。
我们再来看下,eta取值变大会发生什么。
theta_history = [] #初始化全局变量
gradient_descent(initial_theta=0.0,eta=0.8)#为了看得清楚,这里显示标明了参数
plot_theta_history()
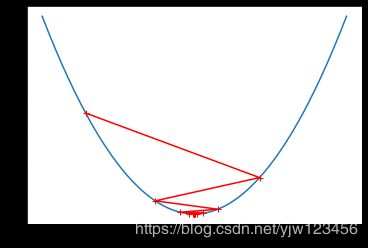
可以看到,此时步伐过大,前面几步直接跳到另一边了,但还不是太大,最终还是收敛得到最小值了。这是否也告诉我们只要能得到最小值,不一样要从一边慢慢的下去?
如果我们再设大一点会怎样呢?
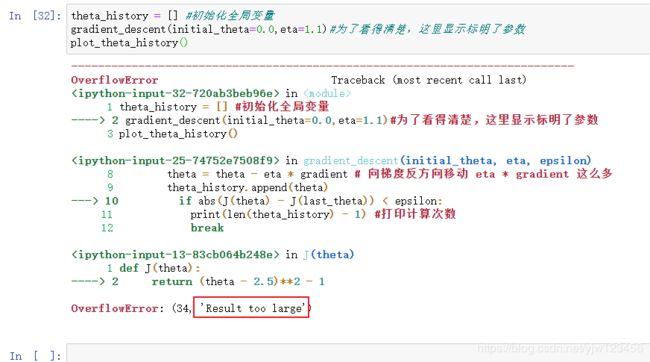
我们设成了1.1,程序直接报错了,因为步伐太大了,这次就没上次那么幸运了,每次都向上跳到另一边,使得损失值不停的增加,由于又是一个死循环,死循环结束的条件还是损失值很小的情况。因此我们要改下我们的代码,可以加个try catch或者设定一个迭代次数:
def J(theta):
try:
return (theta - 2.5)**2 - 1
except:
return float('inf')#返回浮点数的最大值
其实就是在求损失函数值的时候过大,这里我们先改下求损失值的函数,当抛异常时,直接返回浮点数最大值。
这样我们的程序就不会抛出异常了,但是我们的程序将是一个死循环,因为关键点在于循环跳出条件一直无法满足。
在python中abs(J(theta) - J(last_theta)) < epsilon ,如果是无穷大减去无穷大的话,会返回nan(也可以在返回nan的时候跳出循环),并且下面的条件不会满足,因此跑到天荒地老,这段代码也不会结束,除非停水停电。
因此,经过上面的分析,我们不能写成无限循环的形式,一般会设定一个迭代次数:
def gradient_descent(initial_theta,eta,epsilon=1e-8,n_iters = 1e4):
theta = initial_theta
theta_history.append(theta)
i_iter = 0
while i_iter < n_iters: #限定迭代次数
gradient = dJ(theta) # 先求出梯度
last_theta = theta #保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
theta_history.append(theta)
if abs(J(theta) - J(last_theta)) < epsilon:
print(len(theta_history) - 1) #打印计算次数
break
i_iter += 1
这样我们的代码是能终止的,但是此时得到的结果是无法绘制的,因为有无穷大的值:
theta_history = [] #初始化全局变量
gradient_descent(initial_theta=0.0,eta=1.1,n_iters=3)#为了看得清楚,这里显示标明了参数
plot_theta_history()
所以,学习率的取值很重要,过小和过大都不行。
多元线性回归中的梯度下降
在上篇文章中,我们使用了正规方程解来求解多元线性回归的损失函数最小值,并且我们说过正规方程解的弊端。接下来我们就用梯度下降法来求解看。
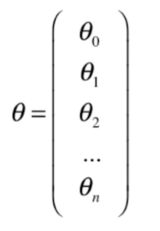
在多元线性回归中,我们的参数有多个,一般用一个向量来表示。上次我们对单个参数 θ \theta θ求导可以写成 d J d θ \frac{dJ}{d\theta} dθdJ,在多元线性回归中我们要写成 ∇ J \nabla J ∇J,这就是梯度,表示对 θ \theta θ向量(还是用 θ \theta θ表示,只不过此时成了向量了 θ = ( θ 0 , θ 1 , ⋯ , θ n \theta =( \theta_0,\theta_1,\cdots,\theta_n θ=(θ0,θ1,⋯,θn)中的 n + 1 n+1 n+1个元素同时求偏导。
∇ J = ( ∂ J ∂ θ 0 , ∂ J ∂ θ 1 , ⋯ , ∂ J ∂ θ n ) \nabla J = (\frac{\partial J}{\partial \theta_0},\frac{\partial J}{\partial \theta_1},\cdots,\frac{\partial J}{\partial \theta_n}) ∇J=(∂θ0∂J,∂θ1∂J,⋯,∂θn∂J)
此时梯度表示J增大最快的方向。
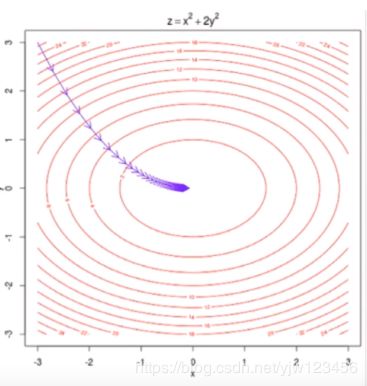
这里对有两个参数的梯度下降法进行了可视化,这一圈一圈的都是等高线。沿着梯度方向的反方向下降的最快。图像中心点达到最小值。
下面我们就来进行推导。
我们的目标是使这个损失函数尽可能小:
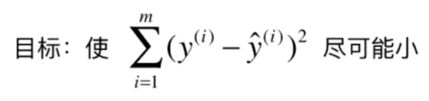
这里的 y ^ i \hat y^i y^i是:
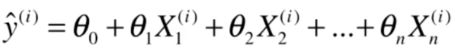
代入上式得:
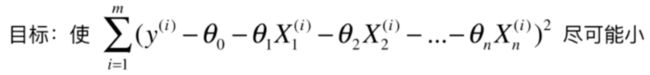
也就是上面的函数就是我们的损失函数 J J J。
此时梯度 ∇ J ( θ ) \nabla J(\theta) ∇J(θ)就是使 J J J对 θ \theta θ的每个维度求偏导,可以写成:
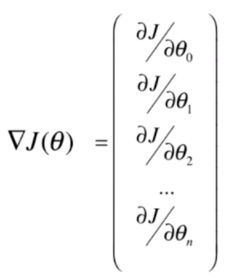
注意这里的 θ 0 \theta_0 θ0其实就是偏置 b b b,对它求偏导就得 − 1 -1 −1。这里我们的 X b X_b Xb是:
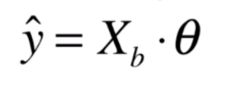
这样我们的梯度就可以写成:
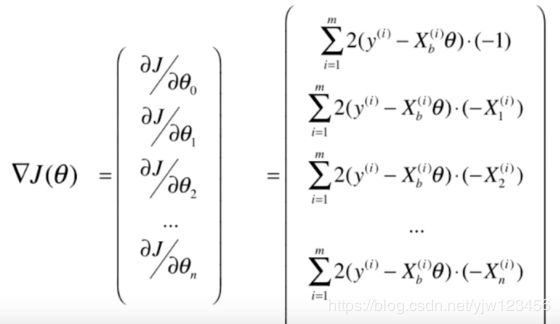
接下来我们整理下上式,我们把求和符号里面的 2 2 2提出来,同时把小括号里面的符号乘到左边括号里面去:

这里还注意到,这里有个求和符号,意味着梯度的大小是与样本数量 m m m有关的,样本数量越大,梯度也就越大。这样显然是不合理的,因此,我们让整个梯度值都除以一个 m m m:

这样相当于把我们的损失函数前面也乘了一个 1 m \frac{1}{m} m1:
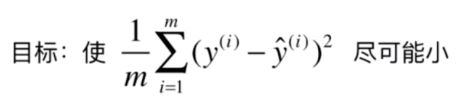
其实这个值就是预测值与真值的MSE:
![]()
有些资料里面 J ( θ ) J(\theta) J(θ)是这样的
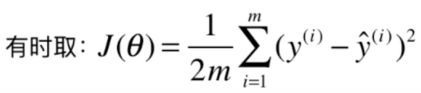
多乘了一个 1 2 \frac{1}{2} 21,其实就是为了越掉上面的系数 2 2 2。
接下来我们通过代码实现下线性回归中的梯度下降法。
通过代码实现线性回归中的梯度下降法
我们先用一个模拟数据来实现下:
import numpy as np
import matplotlib.pyplot as plt
x = 2 * np.random.random(size = 100)
y = x * 3. + 4. + np.random.normal(size=100)
X = x.reshape(-1,1) #把向量x转成矩阵
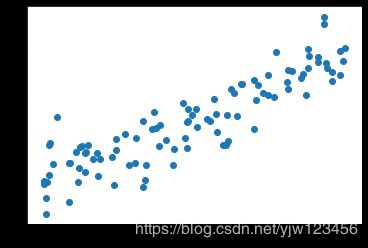
plt.scatter(x,y)
plt.show()
下面我们使用梯度下降法来训练我们的线性回归模型,求得一条拟合直线。
1 m ∑ i = 1 m ( y i − X b i ⋅ θ ) 2 \frac{1}{m} \sum_{i=1}^m ( y^i - X_b^i \cdot \theta)^2 m1i=1∑m(yi−Xbi⋅θ)2
我们还是先来定义损失函数把,公式如上,我们通过代码实现(这里是通过向量化的方式实现的):
def J(theta,X_b,y):
try:
return np.sum((y - X_b.dot(theta))**2) / len(X_b) #
except:
return float('inf')
(y - X_b.dot(theta))**2)我们来看下这个式子中的矩阵的行列数
y(mx1) - X_b ( mx(n+1) ) x theta( (n+1)x1) 得到的是mx1的向量,然后把这个向量每个元素求平方,再求均值得到的是一个标量,没问题。

接下来实现dJ,因为这个式子比 J J J的式子复杂多了,我们先用循环的方式实现:
def dJ(theta,X_b,y):
res = np.empty(len(theta)) #顶一个一个全为0 长度为 len(theta)的向量
res[0] = np.sum(X_b.dot(theta) - y)#特殊处理下 theta_0 ,剩下的n项都有一样的模式
for i in range(1,len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:,i]) #X_b[:,i]是每个样本都取出第i个特征
return res * 2 / len(X_b)
我们还是看下上面代码中每个式子的行列数,利用线代的知识理解一下:
先看下特殊处理的res[0]:X_b.dot(theta) - y 这个式子中是X_b( mx(n+1) ) x theta( (n+1)x1 )) - y( m x 1) 和上面J一样,得到的也是一个向量,求和后得到一个标量。
再看res[i] : (X_b.dot(theta) - y).dot(X_b[:,i]) 中 左边的括号和上面分析过的是一样得到的是一个mx1的向量,我们再看下X_b[:,i]
这里X_b[:,i]是每个样本都取出第i个特征,如果i=1则是下面这样:

从这里可以看到,X_b[:,i]是一个mx1的列向量。
要注意的是我们的 X b X_b Xb表示的是矩阵,J和dJ这两个函数中的X_b也是矩阵。
接下来改写下我们计算梯度的函数,相应地增加X_b,y,同时去掉theta_history,因为在多个维度中,我们也不好绘制图像了。res[i] = (X_b.dot(theta) - y).dot(X_b[:,i]) 这里相当于是两个列向量进行了点乘,即每个元素对应值相乘并相加,最后得到的是一个标量。因此这里是不需要加np.sum()的,加了结果也一样。
下面来验证下两个列向量的点乘结果:

好了,接下来我们修改下梯度下降代码的实现:
def gradient_descent(X_b,y,initial_theta,eta,epsilon=1e-8,n_iters = 1e4):
theta = initial_theta
i_iter = 0
while i_iter < n_iters: #限定迭代次数
gradient = dJ(theta,X_b,y) # 先求出梯度
last_theta = theta #保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
if abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < epsilon:
break
i_iter += 1
return theta #返回计算的结果
现在就可以用我们写的梯度下降法来求线性回归中损失函数的最小值了:
X_b = np.hstack([np.ones((len(X),1)),X]) #先构造我们的X_b
initial_theta = np.zeros(X_b.shape[1]) # theta是个向量
eta = 0.01
theta = gradient_descent(X_b,y,initial_theta,eta) # array([3.9212767 , 3.04245467])
可以看到结果是很接近真实值4,3的
为了把梯度下降的代码添加到我们的线性回归类中,我们先把上面的过程整合到一个函数中:
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
'''
使用梯度下降法进行训练
'''
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dJ(theta, X_b, y):
res = np.empty(len(theta)) # 顶一个一个全为0 长度为 len(theta)的向量
res[0] = np.sum(X_b.dot(theta) - y) # 特殊处理下 theta_0 ,剩下的n项都有一样的模式
for i in range(1, len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:, i]) # X_b[:,i]是每个样本都取出第i个特征
return res * 2 / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta, epsilon=1e-8, n_iters=1e4):
theta = initial_theta
i_iter = 0
while i_iter < n_iters: # 限定迭代次数
gradient = dJ(theta, X_b, y) # 先求出梯度
last_theta = theta # 保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 先构造我们的X_b
initial_theta = np.zeros(X_b.shape[1]) # theta是个向量
self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters=n_iters)
# 分开保存
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
现在线性回归类的完整代码为:
import numpy as np
from sklearn.metrics import r2_score
class LinearRegression:
def __init(self):
self.coef_ = None # 系数
self.interception_ = None # 截距
self._theta = None
def fit_normal(self, X_train, y_train):
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 构造X_b X_train加上 虚构的都等于1的列
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train) # 通过正规方程解求得theta
# 分开保存
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
'''
使用梯度下降法进行训练
'''
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dJ(theta, X_b, y):
res = np.empty(len(theta)) # 顶一个一个全为0 长度为 len(theta)的向量
res[0] = np.sum(X_b.dot(theta) - y) # 特殊处理下 theta_0 ,剩下的n项都有一样的模式
for i in range(1, len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:, i]) # X_b[:,i]是每个样本都取出第i个特征
return res * 2 / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta, epsilon=1e-8, n_iters=1e4):
theta = initial_theta
i_iter = 0
while i_iter < n_iters: # 限定迭代次数
gradient = dJ(theta, X_b, y) # 先求出梯度
last_theta = theta # 保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 先构造我们的X_b
initial_theta = np.zeros(X_b.shape[1]) # theta是个向量
self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters)
# 分开保存
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression(coef_=%s,interception_=%s)" % (self.coef_, self.interception_)
下面我们以上面的X,y来测试一下这个类:
lin_reg = LinearRegression()
lin_reg.fit_gd(X,y)
向量化梯度下降法
上小节我们实现的梯度下降法是通过循环的。

向量化的过程主要集中在求梯度的过程。对于这个式子,我们能否进行向量化,把它们转换为矩阵运算呢。
我们看下这个式子,除了第0项其他项都可以看成是向量点乘的形式。
因此我们把第0项进行统一,让它乘以 X 0 i = 1 X^i_0=1 X0i=1。
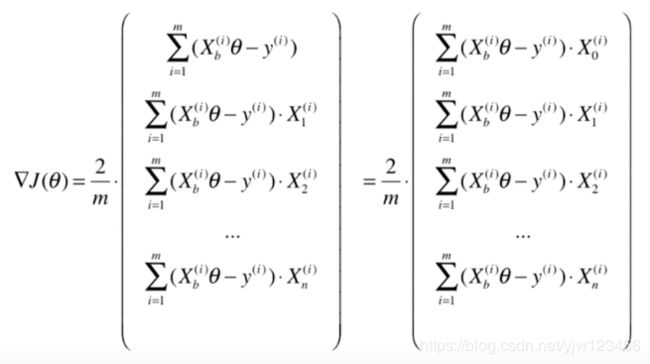
下面我们需要对上图右边的式子进行向量化处理。
其实我们在上小节计算每一项的过程中已经一定程度的向量化了每一项的式子。
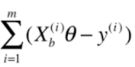
对了该项来说,我们先把它展开,但不进行求和,得到一个1xm的行向量:
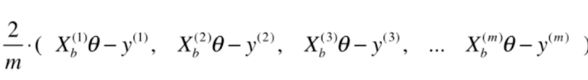
我们再把 X X X展开得到了一个mx(n+1)的矩阵:
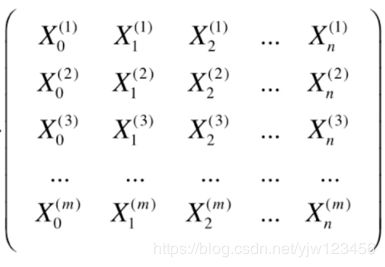
整个式子就是(1xm) x (mx(n+1))得到 1 x (n+1)的行向量,这个行向量中每个维度就是 J J J对每个参数求偏导的值。
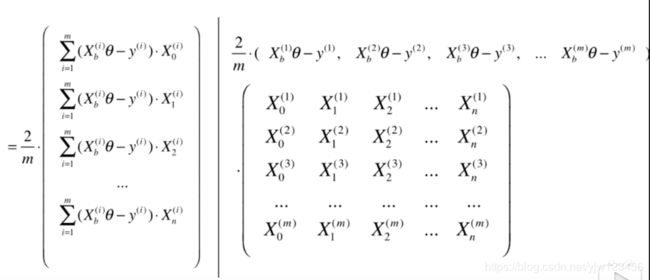
这样我们就把整个过程写成了一个向量和一个矩阵进行运算的形式。
所以最终可以写成:
2 m ⋅ ( X b θ − y ) T ⋅ X b \frac{2}{m} \cdot (X_b \theta - y)^T \cdot X_b m2⋅(Xbθ−y)T⋅Xb
X_b( mx(n+1) ) x θ( (n+1)x1 ) - y(m x 1)) 是m x 1的列向量,图上是行向量的形式,因为我们加了个转置变成列向量1 x m。 而X_b( m x (n+1) ) 。这样我们得到的结果就是 1 x (n+1)的行向量,而我们的梯度其实是(n+1) x 1的列向量。
虽然numpy的表示是不区分行列的,但是为了严谨起见,我们最好还是将最后的式子转换为列向量。也很简单,把整个结果加个转置即可:
( 2 m ⋅ ( X b θ − y ) T ⋅ X b ) T = 2 m ⋅ X b T ⋅ ( X b θ − y ) (\frac{2}{m}\cdot(X_b \theta - y)^T \cdot X_b)^T = \frac{2}{m} \cdot X_b^T \cdot (X_b \theta - y) (m2⋅(Xbθ−y)T⋅Xb)T=m2⋅XbT⋅(Xbθ−y)
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2.0 / len(y)
记得把dJ替换一下。我们来验证一下:

下面我们把我们写的线性回归类用在波士顿房价上。
import numpy as np
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
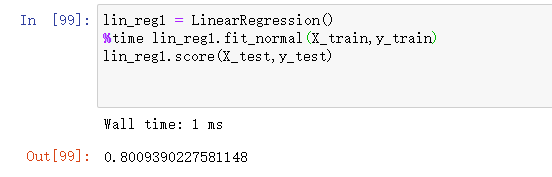
先用上篇文章介绍的正规方程方法来计算下:
lin_reg1 = LinearRegression()
%time lin_reg1.fit_normal(X_train,y_train)
lin_reg1.score(X_test,y_test)
接下来使用梯度下降法:
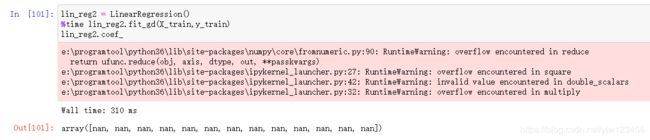
可以看到有一些警告,并且学到的参数都是nan,哪里出问题了呢
用我们自己造的数据来测试没问题,用了真实数据就有问题。那么我们就来看下真实数据长什么样的:
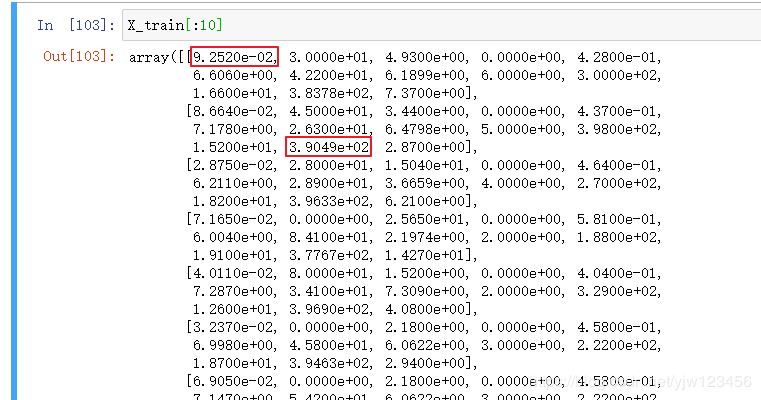
可以看到,每个数据的规模是不一样的,有些是 390 390 390左右,有些只有 0.09 0.09 0.09。
面对这样的数据,我们最终求得的梯度很有可能也是非常大的。我们默认的eta还是太大,为了验证这个假设,我们将eta的值设小一点。
这样我们能计算出来了,但是时间消耗和调用score得到的结果都不理想:
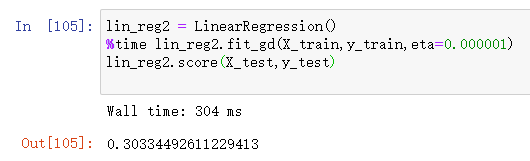
抛开时间消耗不说,我们找到的 θ \theta θ不是使损失函数值最小的那个 θ \theta θ。
这次可能是因为学习率太小导致的。
其实解决的方式很简单,对数据进行归一化即可。
当我们的正规方程法是不需要进行归一化的,这也是这种方法的一个好处。
当我们使用梯度下降法时,由于我们有学习率这个超参数,如果每个维度的数值规模相差很大的话,将会影响梯度的结果,那么这个步长就有可能对某个维度来说太大了,对另一个维度来说又太小了。
如果我们将数据进行归一化,那么这个问题就解决了。接下来我们进行归一化:
from sklearn.preprocessing import StandardScaler
st = StandardScaler()
st.fit(X_train)
X_train_standard = st.transform(X_train)
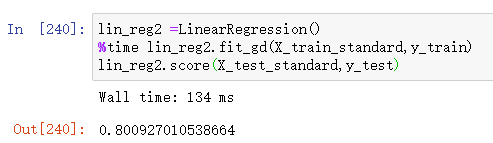
lin_reg3 = LinearRegression()
%time lin_reg3.fit_gd(X_train_standard,y_train)
X_test_standard = st.transform(X_test)
lin_reg3.score(X_test_standard,y_test) #0.800927010538664
得到的结果和使用正规方程的结果差不多。说明我们已经求得了损失函数的最小值。
从消耗时间来看,使用梯度下降法这里耗时虽然不多,但也是远超正规方程的。那么使用梯度下降法到底有什么优势呢?
这里我们模拟一个样本数和特征很多的数据:
m = 1000
n = 10000 #处理图像时的维度通常都会比这大
big_X = np.random.normal(size=(m,n))
true_theta = np.random.uniform(0.0,100.0,size = n + 1)
big_y = big_X.dot(true_theta[1:]) +true_theta[0] + np.random.normal(0.,10.,size=m)
对于这份数据,我们先使用正规方程去解,看它耗时多少:
big_reg1 = LinearRegression()
%time big_reg1.fit_normal(big_X,big_y)
可以看到耗时19秒左右。
我们再用梯度下降的方法来解,由于这里生成的数据是正态分布的,本身就是归一化的,这不需要进行归一化了:
big_reg2 = LinearRegression()
%time big_reg2.fit_gd(big_X,big_y)
因此正规方程的解法处理大矩阵时是没有什么优势的。
细心的同学可能会发现,我们样本的数量是小于特征的数量的。我们现在的梯度下降法在计算公式时,需要每个样本都来参与计算,这样当样本量很大时,我们计算梯度会变成更慢。对于这个问题,可以用随机梯度下降法来改进。
随机梯度下降法
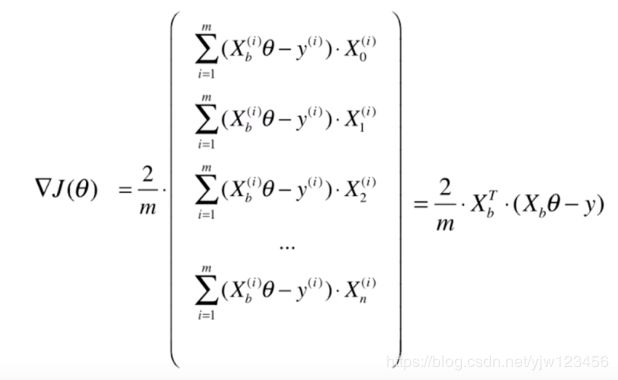
我们上面求梯度下降法时是用到了所有的样本的(总样本数为m)。从上面的公式也可以看出来,我们对所有的样本进行计算。这样的梯度下降法称为批量梯度下降法(Batch Gradient Descent)。
如果样本量非常大时,计算梯度本身也是很耗时的。基于这个问题,一种显然的改进方案是每次更新梯度时并不需要看完所有的样本。夸张一点的话,我们每次只看一个样本,这种方法称为随机梯度下降法(Stochastic Gradient Descent)
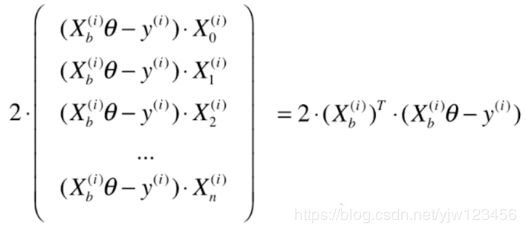
这里的 X i X^i Xi就是我们随机选取的一个样本,公式也就简化为如上。我们基于这个公式给出的方向进行搜索(此时的搜索方向不是梯度的方向了)会有怎么的效果呢。
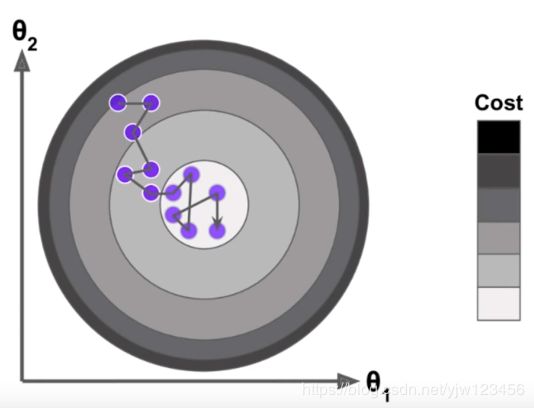
随机梯度下降法的搜索过程如上图所示,由于随机梯度下降法无法保证得到的方向一定是损失函数减小的方向,更不能保证是减小最快的方向,所以我们的搜索路径形成了这样的一种趋势。也就是它具有随机的特点,但是实验结论告诉我们,它最终依然可能到达最小值的附近。
当样本数很大时,用精度换取时间是有意义的。
在随机梯度下降法中,学习率的取值很重要。如果我们已经来到了最小值中心的位置了,但是随机的过程不够好,如果学习率是一个固定值的话,有可能会跳出最小值的区域。
所以在实际的随机梯度下降法中,我们期望我们的学习率是逐渐递减的。我们可以设计一个函数,让学习率随着迭代次数的增加而变小。
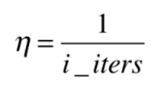
最简单的方法就是迭代次数的倒数。但是当我们的学习率较小的时候,这个函数会导致学习率下降过快。所以通常我们会增加一个常数 b b b:
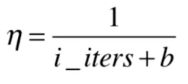
这个常数可以取50,当我们的循环次数从0上升到2的时候,我们的学习率只会下降2%左右,这样可以缓解我们在初始迭代的时候下降过快。
在分子的位置,我们也设一个常数 a a a:
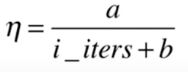
a , b a,b a,b都是超参数,这样 a a a会比 1 1 1灵活一些,我们可以手动调整。
实际上这种逐渐递减的思路就是模拟退火的思想。比如说打造钢铁时火焰的温度是由高到底逐渐冷却的,这个冷却的函数是和时间相关的,所以很多时候可以用与时间有关的 t 0 , t 1 t_0,t_1 t0,t1来表示上式:
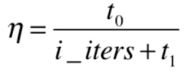
下面我们通过代码来实现随机梯度下降法。
我们首先改一下dJ:
def dJ_sgd(theta, X_b_i, y_i):
"""X_b_i 只是一个样本 y_i也只是一个数值"""
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2.0
因为我们每次只传一个样本和它对应的预测值进去了。
接下来实现随机梯度下降法主要过程:
def sgd(X_b,y,initial_theta,n_iters):
t0 =5
t1 = 50
# 学习率函数
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b)) #随机一个索引
gradient = dJ_sgd(theta,X_b[rand_i],y[rand_i])
theta = theta - learning_rate(cur_iter) * gradient #每次的随机率都是递减的
return theta
因为搜索方向是随机的,哪怕两次损失值相差很少,也不一定代表到达了最小值。因此我们去掉了这个判断,改成通过迭代次数来控制退出。
下面我们来测试一下,首先准备数据:
m = 100000
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 4.0 * x + 3.0 + np.random.normal(0,3,size=m)
然后测试一下:
%%time
X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b,y,initial_theta,n_iters=len(X_b)//3)# 这里设置的循环次数为样本个数除以3
theta
这里设置的循环次数为样本个数除以3,意思是比批量梯度下降法一次计算的样本个数都要少,我们看下结果如何:
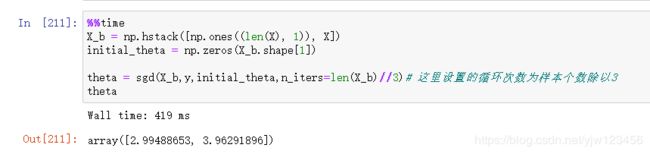
哇,结果不错,时间419ms算不算多呢,我们先把这个算法封装到我们的类中,再与批量梯度算法对比一下。
在我们之前的类中增加:
def fit_sgd(self, X_train, y_train, initial_theta, n_iters, t0=5, t1=50):
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters, t0, t1):
# 学习率函数
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b)) # 随机一个索引
gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter) * gradient # 每次的随机率都是递减的
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
测试:
m = 1000000 #用10W结果不明显,我改成了100W
x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 4.0 * x + 3.0 + np.random.normal(0,3,size=m)

可以看到,最终求得的最小值参数差不多,但是时间相差还是蛮大的。
sklearn中的随机梯度下降法
在介绍sklearn中的随机梯度下降法前,先用真实数据来测试一下我们的类。
在上节中为了显示随机梯度下降法的优势,故意将迭代次数设置为样本总数除以3,这种方式其实是不科学的。更加科学的方式是至少看一遍所有的样本。
为什么要看一遍所有样本,可能你的模型没看到的样本刚好是关键的那些样本,那么此时你的模型就很可能是欠拟合的了。
那么此时,迭代次数具体取多少就不是那么容易定了,因为要看一遍所有的样本,如果样本数过大,而迭代次数过少,显然是看不完的。
所以通常在随机梯度下降法中,迭代次数描述的成了要看几轮样本(一轮就可以看完所有样本)。一般这个次数可以默认设成5。
这里所谓的洗牌其实就是乱序排序,通常在洗牌时要保证别人无法猜到洗牌后的顺序(伪随机数根据时间种子可以推断出来),因此洗牌算法一般不是简单的随机。
现在问题是要保证能看完所有的样本,因此我们的随机索引的取法也要改变,常用的做法是对整个样本点索引值进行一次洗牌操作,然后根据洗牌后的索引顺序进行遍历。
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters, t0, t1):
# 学习率函数
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b) #整个样本数
for cur_iter in range(n_iters): #外层循环代表要看几轮
indexes = np.random.permutation(m) #对索引进行洗牌操作
for i,rand_i in enumerate(indexes): # i 代表这一轮中第几次遍历, rand_i是随机索引
gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter * m + i) * gradient # 每次的随机率都是递减的,cur_iter从0开始,现在要这么计算了
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
最终改造好的随机梯度下降法如上所示。这里还是再贴一次完整的代码吧:
import numpy as np
from sklearn.metrics import r2_score
class LinearRegression:
def __init(self):
self.coef_ = None # 系数
self.interception_ = None # 截距
self._theta = None
def fit_normal(self, X_train, y_train):
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 构造X_b X_train加上 虚构的都等于1的列
self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train) # 通过正规方程解求得theta
# 分开保存
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
def sgd(X_b, y, initial_theta, n_iters, t0, t1):
# 学习率函数
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b) #整个样本数
for cur_iter in range(n_iters): #外层循环代表要看几轮
indexes = np.random.permutation(m) #对索引进行洗牌操作
for i,rand_i in enumerate(indexes): # i 代表这一轮中第几次遍历, rand_i是随机索引
gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter * m + i) * gradient # 每次的随机率都是递减的,cur_iter从0开始,现在要这么计算了
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.random.randn(X_b.shape[1])
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
'''
使用梯度下降法进行训练
'''
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2.0 / len(y)
def gradient_descent(X_b, y, initial_theta, eta, epsilon=1e-8, n_iters=1e4):
theta = initial_theta
i_iter = 0
while i_iter < n_iters: # 限定迭代次数
gradient = dJ(theta, X_b, y) # 先求出梯度
last_theta = theta # 保存之前的theta
theta = theta - eta * gradient # 向梯度反方向移动 eta * gradient 这么多
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
i_iter += 1
return theta
X_b = np.hstack([np.ones((len(X_train), 1)), X_train]) # 先构造我们的X_b
initial_theta = np.zeros(X_b.shape[1]) # theta是个向量
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters=n_iters)
# 分开保存
self.interception_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
def predict(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return X_b.dot(self._theta)
def score(self, X_test, y_test):
y_predict = self.predict(X_test)
return r2_score(y_test, y_predict)
def __repr__(self):
return "LinearRegression(coef_=%s,interception_=%s)" % (self.coef_, self.interception_)
因为改了代码,我们现在模拟数据上测试:

这次耗时还是快了一倍左右,随机梯度下降法总共看了2轮样本。
接下来用真实数据进行测试:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 加载波士顿房价数据
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
# 归一化
st = StandardScaler()
st.fit(X_train)
X_train_standard = st.transform(X_train)
X_test_standard = st.transform(X_test)
接下来先用随机梯度下降法:
lin_reg =LinearRegression()
%time lin_reg.fit_sgd(X_train_standard,y_train,n_iters=2)
lin_reg.score(X_test_standard,y_test)
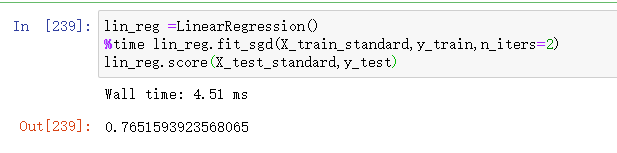
这个分数之前有0.8左右,显然只看两轮达到的效果不是很好,因此我们增加轮数看看效果会不会更好。
再用批量梯度下降法试一次:
lin_reg2 =LinearRegression()
%time lin_reg2.fit_gd(X_train_standard,y_train)
lin_reg2.score(X_test_standard,y_test)
接下来我们看下sklearn中的随机梯度下降法。
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor()
%time sgd_reg.fit(X_train_standard,y_train)
sgd_reg.score(X_test_standard,y_test)
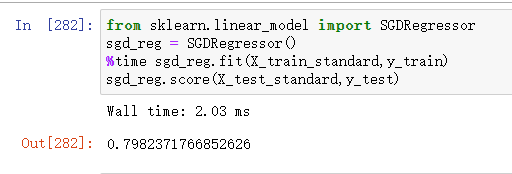
可以看到,哪怕只是使用默认的参数,得到的效果和耗时都是很好的。sklearn为我们优化了不少啊。
参考
1.Python3入门机器学习
- 上一篇:机器学习入门——线性回归详细分析
- 下一篇:机器学习入门——详解主成分分析