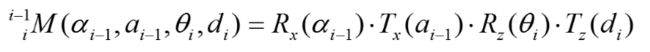学习笔记之——Jacobian matrix（雅可比矩阵）

在《斯坦福大学公开课——机器人学》视频课程中一开始就提到了Jacobian matrix的重要性。为此写下本学习笔记介绍雅可比矩阵。本博客的内容来自于网络的各种资料的总结，已经给出参考引用。本文仅作本人学习记录用。

 

目录

定义

机器人关节（Joint）之间的坐标变换（Transform）

Jacobian Matrix 在运动学中的意义

Jacobian Matrix 在正运动学中的应用

Jacobian Transpose 在力和力矩中的应用

参考资料

---

 

定义

在向量微积分中，雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数。

在向量分析中，雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。

在代数几何中，代数曲线的雅可比行列式表示雅可比簇：伴随该曲线的一个代数群，曲线可以嵌入其中。

 

假设某函数从映到， 其雅可比矩阵是从到的线性映射，其重要意义在于它表现了一个多变数向量函数的最佳线性逼近。因此，雅可比矩阵类似于单变数函数的导数。

 

假设是一个从n维欧氏空间映射到到m维欧氏空间的函数。这个函数由m个实函数组成：。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵，这个矩阵就是所谓的雅可比矩阵：

此矩阵用符号表示为：，或者

这个矩阵的第 i行是由梯度函数的转置表示的如果p是中的一点，F在 p点可微分，根据高等微积分，是在这点的导数。在此情况下，这个线性映射即F在点p附近的最优线性逼近，也就是说当x足够靠近点p时，有

 

总结一下，雅可比矩阵可以理解为：

若在n维欧式空间中的一个向量映射成m维欧式空间中的另一个向量的对应法则为F，F由m个实函数组成，即：

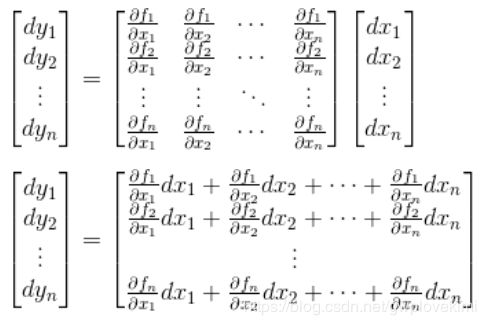
那么雅可比矩阵是一个m×n矩阵：

其中，雅克比矩阵就是这个变换对应的偏导而组成的矩阵。输入向量x = (x1, ... , xn)，输出向量y = (y1, ..., ym)，

如果p是中的一个点，F在p点可微分，根据数学分析，雅可比矩阵是在这点的导数。在此情况下，这个线性映射即F在点p附近的最优线性逼近，也就是说当 x足够靠近点 p时，我们有

当m = n时，矩阵就会变成一个方阵，F就变成从n维欧式空间到n维欧式空间的映射，方阵的行列式就是雅可比行列式。上式移项得：

即：

和 是向量，n维空间的向量，那么微分的话，就是相等的了：

其中： 

即：

将上述向量写成基于正交的单位向量的形式：

行列式的绝对值表示微元的体积，左侧行列式一定为正，体积不可能为负，右侧行列式加绝对值

将公共因数提出

即，此微元的体积为:

 

机器人关节（Joint）之间的坐标变换（Transform）

之前博客《ROS学习笔记之——ROS之tf变换》已经介绍过机器人的tf编码，这里再对其理论进行描述，从而有利于下面介绍雅克比矩阵在正运动学中的推导和应用

对于人体动画来说，坐标变化是非常简单的，只要在当前关节乘上该节点旋转矩阵和子节点偏移矩阵，就可以完成父节点到子节点的坐标变换。其中变换矩阵（Transform）为M=R·Toffset。但是机器人的坐标变换就没有那么简单了，机器人相比人要复杂，主要体现在两个方面：（1）人的关节是一个球形结构，具有三个自由度；而机器人的关节一般只有一个自由度，所以用机器人模拟人的手腕需要三个关节。（2）人关节之间是由手臂连起来的，在转动的过程中两个关节之间的距离是不会变的；而机器人的关节之间连接情况比较复杂。

坐标变换分为两步：1、选取D-H参数；2、建立关节的笛卡尔坐标系

先介绍一下D-H参数（Denavit-Hartenberg Parameters）。如下图所示

这是两个旋转关节分别绕Axis i-1和Axis i进行旋转，其位置分别是1和2。这里可以看出，两个关节不是直接连在一起的，而且两个关节之间的连杆的长度也可能是不固定的或者说不是直线。这就不能像人体动画中直接乘上旋转矩阵和偏移矩阵来进行坐标变换。这看起来相当复杂，但是由于D-H参数的出现，这导致坐标变换变得相当直观简单。这里我们结合上图介绍一下D-H参数一共有哪几种，都是什么涵义：

1. αi-1，Axis i-1和Axis i之间的夹角。
2. ai-1，Axis i-1和Axis i之间的距离。
3. θi，ai-1和ai之间的的夹角。（这里ai指得是Axis i和Axis i+1之间的距离）
4. di，ai-1和ai之间的的距离。（可以理解为ai-1和ai分别与Axis i交点之间的距离，因为ai-1和ai分别与Axis i垂直）

αi-1和ai-1用来描述连杆的性质，而θi和di用来描述连杆之间的连接状态。

接下来建立关节的笛卡尔坐标系。所建立的坐标系如下图所示。建立坐标系首先要确定原点，观察可以得到，原点选在Axis i-1和ai-1的交点位置是最好的。这样我们z轴就可以沿着Axis i-1，而x轴也可以沿着ai-1。然后确定y轴，其肯定等于x轴和z轴的叉乘，也就是y轴的位置已经是确定了，方向可以根据右手坐标系确定。这里提一点，αi-1可以看做两个z轴的夹角，ai-1可以看做两个z轴的距离，θi可以看做两个x轴的夹角，di可以看座是两个x轴的距离。

最后就可以进行坐标变换了。坐标变换主要分为4个环节（如下图所示）：

1. 将Axis i-1绕ai-1轴（x轴）旋转αi-1。（因为ai-1分别垂直于Axis i-1和Axis i）
2. 将Axis i-1沿ai-1轴（x轴）方向平移ai-1。
3. 将Axis i-1绕Axis i轴（z轴）旋转θi。（因为Axis i分别垂直于ai-1和ai）
4. 将Axis i-1沿Axis i轴（z轴）方向平移di。

这样就将Axis i-1转换成了Axis i。再根据这四个变换可以得到Axis i-1转换成Axis i的旋转矩阵M。具体公式如下：

 

Jacobian Matrix 在运动学中的意义

先假设已知的先验知识，如：机械臂是由一些关节（Joint）连接的，一直从基座（base）连接到末端执行器（End-Effector）。如下图所示，关节一般只有一个自由度（要么是旋转，要么是平移），末端执行器有六个自由度。那么如何通过每一个关节的自由度求出末端执行器的角速度和线速度呢？。这里在引入瞬时动力学的概念。即：任意关节运动，末端执行器也会跟着运动，如果时间足够小的话，可以看作关节和末端执行器都是瞬时变化的。那么问题也就转变成找ΔQ（关节的变化）和ΔX（末端执行器的变化）之间的关系。

对于旋转关节（revolute）一般讨论的是角度的变化，对于平移关节（prismatic）一般讨论的是距离的变化。这里为了统一表示，我们将角度和距离统称为通道量，记为q。同时，我们将目标状态（就是指末端执行器的角速度和线速度）记为向量组X={x1，x2，x3，x4，x5，x6}。X中的每一个元素都是由q求出来的，记为x=f(q)。这样可以得到一组等式：（下面等式类似于上文介绍雅可比矩阵时，提及到的：若在n维欧式空间中的一个向量映射成m维欧式空间中的另一个向量的对应法则为F）

对上式进行扩展，对X中的每一项进行全微分，等式的右边对所有的q进行偏导。展开式如下 ：

其中，右边的矩阵就是本博文前面所提到的Jacobian matrix。Jacobian matrix的行等于X中的项数m，也就是末端执行器的自由度个数，而矩阵的列等于Q中的项目数，也就是关节的个数。简写为下面：

雅克比主要联系的是ΔQ（关节的变化）和ΔX（末端执行器的变化），是瞬时运动学的重要组成部分。这就是为什么雅克比矩阵在运动学中如此的重要！

在机器人学中，雅克比矩阵主要是用来求末端执行器的角速度和线速度（ΔX），ΔQ和ΔX在微分的情况下是可以用来表示速度的。在逆运动学中，则可以通过利用末端执行器的自由度反算每个节点的自由度，也即：只要将ΔX乘以雅克比矩阵的逆就可以得到Q的变化了。

 

Jacobian Matrix 在正运动学中的应用

运动主要是计算位置信息和速度信息的变化。所以对于机械臂来说，最终想得到的也就是末端执行器的位置和速度。本节中介绍一下，采用正运动学求末端执行器的线速度和角速度。关节分为旋转关节和平移关节，那么这两种关节分别对线速度和角速度的影响如下图所示

平移关节对末端执行器的角速度是没有影响的；平移关节沿自身的Z轴移动，对末端执行器的线速度提供一个Z轴方向的分速度。旋转关节对末端执行器的角速度也是提供一个分量，角速度分量的方向也是沿Z轴的。而对于旋转关节对末端执行器的线速度的影响为——Ωi和Pin的叉乘的结果等于vp。这也就是旋转关节对于末端执行器线速度的影响。

接下来通过雅可比矩阵来看看每个关键对于末端执行器线速度和角速度的影响

Vi和Ωi可表示为，这两个量就是通道量乘上其方向向量：

根据Vi和Ωi，可以写出末端执行器的角速度和线速度的公式如下：

这里，ε有两个值0和1，当ε表示的是平移矩阵的时候值为1，表示的是旋转矩阵的时候值为0。这样就得到线速度和角速度的公式，而根据上一节描述，线速度和角速度可以看作微分的形式，进而再次引入Jacobian matrix，扩展公式有：

这样就得到了末端执行器的角速度和线速度跟各关节通道q之间的关系。那么整个Jacobian matrix则是

利用雅可比矩阵，就可以得到了通道q和末端执行器的线速度v以及角速度ω之间的关系

 

Jacobian Transpose 在力和力矩中的应用

雅克比矩阵可以由给出的关节速度求解末端执行器的速度，除此之外，雅克比矩阵还可以体现末端执行器上施加的力和关节上施加的力矩之间的关系。

首先介绍两个基本的原理

• 虚功原理：对于一个物体，只需要考虑主动力，不用管所有的内力，因为内力是由结构产生的，这种力并不能使物体产生移动。而对于一个静态平衡的系统，所有外力的作用，经过虚位移，所作的虚功，总和等于零。
• 叉乘矩阵：叉乘前面的向量可以转化成一个矩阵，我们称这个矩阵为叉乘矩阵，可以看出这是一个反对称矩阵。其最重要的性质就是。

如下图所示，可以类似线速度和角速度的关系，用叉乘的方式表示出力和力矩之间的关系。

根据叉乘矩阵的性质，可以做进一步推导，就可以得到两个机器人最基础的公式，具体如下：

根据虚功原理，对末端执行器进行虚位移，由于虚功总和为0，有：

这样就可以通过雅克比矩阵的转置把力和力矩联系在一起。

 

参考资料

https://baike.baidu.com/item/%E9%9B%85%E5%8F%AF%E6%AF%94%E7%9F%A9%E9%98%B5/10753754?fromtitle=%E9%9B%85%E5%85%8B%E6%AF%94%E7%9F%A9%E9%98%B5&fromid=5726542&fr=aladdin

https://www.cnblogs.com/caster99/p/4725914.html?utm_source=tuicool&utm_medium=referral

https://www.cnblogs.com/caster99/p/4717358.html

https://www.cnblogs.com/caster99/p/4703033.html

https://www.cnblogs.com/caster99/p/4733988.html

https://www.cnblogs.com/rswss/p/11440144.html

https://www.zhihu.com/question/22586361

https://www.bilibili.com/video/av4506104?t=836