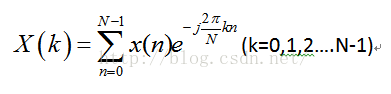数字信号处理②之从傅里叶系数到DFT

---

• 数字信号处理系列博客：

• 数字信号处理之信号的合成、分解、相关性及傅里叶系数的计算

• 数字信号处理之从傅里叶系数到DFT

---

---

一、前言

• 信号与系统课程学了一遍傅里叶变换，数字信号处理课程学了一遍离散傅里叶变换和快速傅里叶变换，但是现在谈到傅里叶变换也未能够一语道出他的本质和精髓，我觉得对于这个在数字信号处理领域有着元老地位的傅里叶变换仅仅是了解是不够的，因为我发现在进行很多数字信号处理时这个理论往往很有用，能够突破常规思维另辟独特的解决方法，本文将以最简单的思维方式去讨论如何从傅里叶系数推导到DFT。

---

二、对合成信号进行各次谐波分析

• 从上一篇文章我们知道，欲求一个信号中某种频率的分量，只要将这个信号与欲求频率的信号作相关，即相乘求积分就能够得到这个信号中欲求频率所占的分量。

（一）合成信号

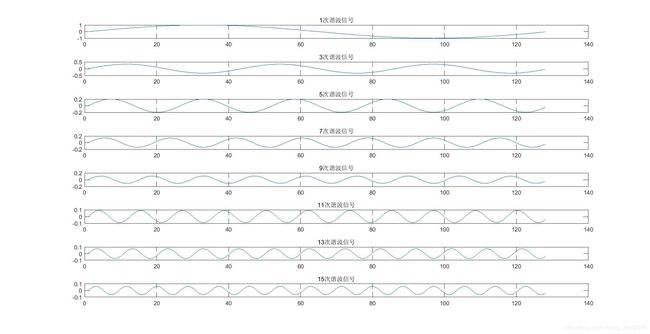
• 在上一篇文章中，我们通过正弦波奇次谐波的叠加合成了方波，这一次为了使结果更明显同时也为了计算方便，我们将谐波增加到15次，看起来感觉更像方波了，同时使用for循环替代了原来的操作，看起来更简便

M=15;%谐波次数
sine=zeros(M,N);%各次谐波存放的矩阵
square=zeros(1,N);%存放合成方波
figure(1);
for i=1:2:M
    sine(i,:)=sin(2*pi*i*f*t)/i;%生成i次谐波
    square=sine(i,:)+square;%将谐波叠加
    subplot(M,1,i);
    plot(sine(i,:));
    title(sprintf('%d次谐波信号',i));
end
clear i;%清除临时变量i
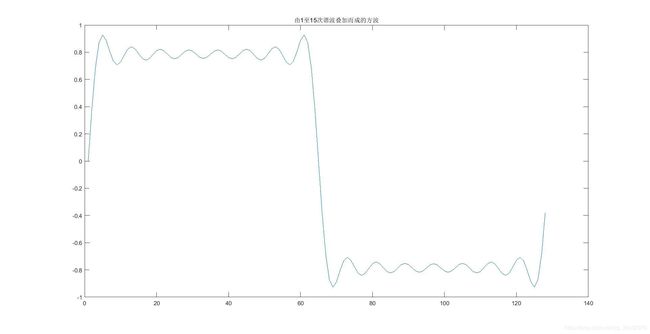
figure(2);
plot(square);
title(sprintf('由1至%d次谐波叠加而成的方波',M));

（二）使用复指数代替正弦余弦

• 由欧拉公式

• 可以知道，cos(wt)和sin(wt)两个相关函数可以用指数e的形式来代替，这样可以简化运算

（三）用指数信号与合成信号作相关进行各次谐波分析

• 将合成信号与相关函数相乘

y_dft(1,:)  =  dft_exp(f,0*w,t);
y_dft(2,:)  =  dft_exp(f,1*w,t);
y_dft(3,:)  =  dft_exp(f,2*w,t);
y_dft(4,:)  =  dft_exp(f,3*w,t);
y_dft(5,:)  =  dft_exp(f,4*w,t);
y_dft(6,:)  =  dft_exp(f,5*w,t);
y_dft(7,:)  =  dft_exp(f,6*w,t);
y_dft(8,:)  =  dft_exp(f,7*w,t);
y_dft(9,:)  =  dft_exp(f,8*w,t);
y_dft(10,:) =  dft_exp(f,9*w,t);
y_dft(11,:) =  dft_exp(f,10*w,t);
y_dft(12,:) =  dft_exp(f,11*w,t);
y_dft(13,:) =  dft_exp(f,12*w,t);
y_dft(14,:) =  dft_exp(f,13*w,t);
y_dft(15,:) =  dft_exp(f,14*w,t);
y_dft(16,:) =  dft_exp(f,15*w,t);

• 求和

Y_DFT(1)  = sum_len(y_dft(1,:) ,N)/N;
Y_DFT(2)  = sum_len(y_dft(2,:) ,N)/N;
Y_DFT(3)  = sum_len(y_dft(3,:) ,N)/N;
Y_DFT(4)  = sum_len(y_dft(4,:) ,N)/N;
Y_DFT(5)  = sum_len(y_dft(5,:) ,N)/N;
Y_DFT(6)  = sum_len(y_dft(6,:) ,N)/N;
Y_DFT(7)  = sum_len(y_dft(7,:) ,N)/N;
Y_DFT(8)  = sum_len(y_dft(8,:) ,N)/N;
Y_DFT(9)  = sum_len(y_dft(9,:) ,N)/N;
Y_DFT(10) = sum_len(y_dft(10,:),N)/N;
Y_DFT(11) = sum_len(y_dft(11,:),N)/N;
Y_DFT(12) = sum_len(y_dft(12,:),N)/N;
Y_DFT(13) = sum_len(y_dft(13,:),N)/N;
Y_DFT(14) = sum_len(y_dft(14,:),N)/N;
Y_DFT(15) = sum_len(y_dft(15,:),N)/N;
Y_DFT(16) = sum_len(y_dft(16,:),N)/N;

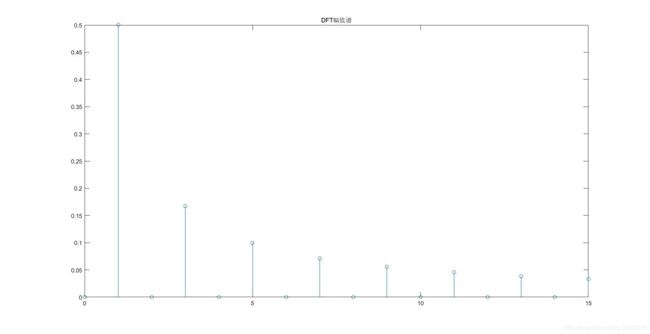
stem(0:15,abs(Y_DFT));
title('DFT幅值谱');

• 可以看到1、3、5、7、9、11、13、15次谐波的幅值，和叠加前的幅值是一样的，而0、2、4、6、8、10、12、14次谐波因为合成信号时并没有输入，所以其值都为零
• 接下来看一下相位谱

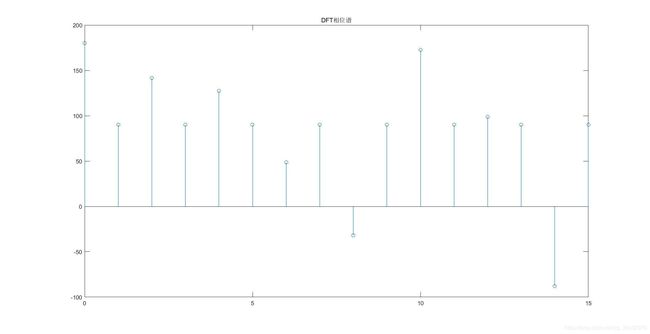
stem(0:15,angle(Y_DFT)*180/pi);
title('DFT相位谱');

• 可以看到1、3、5、7、9、11、13、15次谐波的相位都是90度，与输入信号相位相同，而0、2、4、6、8、10、12、14次谐波因为输入为零，所以输出的信号实部和虚部都趋近于零，对它求相位其实是没有意义的

回到顶部

---

三、从傅里叶系数到DFT

（一）FT、DTFT、DFT

• FT（Fourier transform）是傅里叶变换，他是将连续的时域信号变换到连续的频域信号的工具，但是应为时域和频域都是连续的信号，而数字系统只能够处理离散的信号，所以FT无法在数字系统中使用。
• DTFT（Discrete Time Fourier Transform）离散时间傅里叶变换，它是将连续的时域信号通过采样进行离散化后，再变换到频域的工具，但是频域信号依然是连续的，数字系统无法处理。
• DFT（Discrete Fourier Transform）离散傅里叶变换，它是将将连续的时域信号通过采样进行离散化后，变换到频域信号，再将频域信号通过采样进行离散化，得到离散的频域信号，因为其时域信号和频域信号都是离散的，可以很方便计算机进行计算，所以相对于前两者它是在数字系统中运用最广的。

（二）从傅里叶系数到DFT

• 仔细观察DFT的公式，然后回忆前面我们进行的步骤

  • k=1时，将x(n)这个序列与e^(-2πkn/N)相乘，然后求积分
  • k=3时，
  • k=5时，
    …
    

• 仔细一想，会发现k=1时对应1次谐波，k=3时对应3次谐波，k=5、7、9…

• 其实我们之前作的就是DFT，只不过是我们知道了原信号中有哪些频率分量，所以我们只要要用什么频率去作相关，而对于DFT，我们并不知道原信号中含有那些频率分量，所以我们需要更多的频率都拿来做相关，但是这个频率到底需要多少呢？于是我们规定一个间隔，每个多少进行一次采样，只要保证我们这个间隔足够小，我们就能分别出原信号中的相差足够小的频率分量，这个间隔，就叫做频谱分辨率。

• 关于频谱分辨率，你会发祥它不仅与DFT的点数有关，还与采样率有关，只要记住

$$频谱分辨率=采样率÷采样点数$$

• 前面我们分析过了，DFT就是对原信号进行信号的相关，也就是对原信号乘以一个欲知频率的复指数信号然后求和求均值。为了保证足够的分辨率并且方便进行频谱分析，我们将采样点数设置成128，基波频率设置成1Hz，采样率设置成128Hz，那么频谱分辨率就是128Hz÷128=1Hz。为了得到完整的DFT频谱，我们用频率为[0:1:127]（最小值是0，最大值是127，步进1，标准的matlab写法）的复指数信号去与原信号作相关。

y_dft=zeros(N,N);%合成信号与相关信号相乘后存放到这里
for i=0:N-1
    y_dft(i+1,:)  =  dft_exp(square,i*f,t);
end

• 求和

Y_DFT=zeros(1,N);%DFT频谱
for i=0:N-1
    Y_DFT(:,i+1)  = sum_len(y_dft(i+1,:) ,N)/N;
end

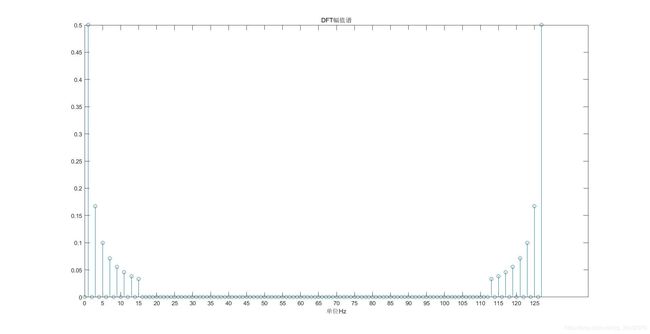
• 画出幅度谱

stem(0:N-1,abs(Y_DFT));
set(gca,'XTick',0:10:N-1);
title('DFT幅值谱');

• 可以看到各次谐波的分量值，正好是之前输入的值
• 关于右边为什么会有一个对称的频谱，这个其实用最简单的思维来理解就是这样的，由于我们设置的采样率只有128Hz，根据奈奎斯特采样定理，我们能够采样的最大不失真信号的频率就是128÷2=64Hz，也就是说从64Hz到127Hz的频谱是由于采样时产生的失真引入的，所以实际上这部分频谱并没有意义，也就是说我们只需要关心0到64Hz的频谱就行了，同时我们的频谱域就限制在了64Hz

---

最后

• 本文仅仅是以最简单的思维方式来讨论它的本质及实现，但在实际应用过程中还有很多地方需要注意，例如栅栏效应、频谱泄露、频域混叠、窗函数等等。
• 关于FFT（fast Fourier transform），它本质上就是DFT，只不过它根据DFT运算过程中旋转因子的奇、偶、虚、实、对称等特性，简化了计算量
• 关于DFT，它的作用就是将时域信号转换到频域信号，给人们提供了另一种独特的方式去观察信号，与其说它是一种工具，不如说它是人们的第三只眼睛，让人们拥有更强大的能力去观察世界。
• 最后送上一句，纸上得来终觉浅，绝知此事要躬行。

---

声明：本文仅作为个人技术交流，所述如有不当之处，欢迎读者批评指正！
转载请注明出处：https://blog.csdn.net/qq_39432978/article/details/89411438

---

回到顶部