数论学习笔记

引用自

https://www.cnblogs.com/zyf3855923/category/1167779.html

1.素数唯一分解定理

单个素数判定方法：枚举所有小于数，看是否它能整除其他自然数，但实际上只需要枚举根号次。

代码实现

bool Is_prime(int n)
{
    for(int i=2;i*i<=n;++i)
    {
        if(n%i==0) return false;
    }
    return true;
}

暴力复杂度

两种筛法

• 埃氏筛：做法其实很简单，首先将2到n范围内的整数写下来，其中2是最小的素数。将表中所有的2的倍数划去，表中剩下的最小的数字就是3，他不能被更小的数整除，所以3是素数。再将表中所有的3的倍数划去……以此类推，如果表中剩余的最小的数是m，那么m就是素数。然后将表中所有m的倍数划去，像这样反复操作，就能依次枚举n以内的素数，这样的时间复杂度是O(nloglogn)。

代码实现

#include 
#include 
using namespace std;
const int N=1000005;
int prime[N];
bool vis[N];
int cnt;
void judgeprime(int n)
{
    for(int i=2;i*i<=n;i++)
    {
        if(!vis[i]) prime[cnt++]=i;
        for(int k=i+i;k<=n;k+=i)
            vis[k]=true;
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    judgeprime(n);
    for(int i=2;i

• 欧拉筛：欧拉筛法的基本思想 ：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。其他复杂度（O(n)）.
  代码实现

#include 
#include 
using namespace std;
int n;
int prime[10000005];
bool vis[10000005];
int cnt;
void primejudge(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]) prime[cnt++]=i;
        for(int k=0;k

-米勒罗宾素数检测法：基于随机算法，可以在O(logn)内判断一个数是否是素数，但存在一定的误差。（1e18内认为无误差）
代码实现

#include 
#define maxn 10005
using namespace std;
typedef long long LL;
const int inf= 1e9;
struct Miller_Rabin
{
    LL prime[6] = {2, 3, 5, 233, 331};
    LL qmul(LL x, LL y, LL mod) {
        return x*y%mod;
        return (x * y - (long long)(x / (long double)mod * y + 1e-3) *mod + mod) % mod;
    }
    LL qpow(LL a, LL n, LL mod) {
        LL ret = 1;
        while(n) {
            if(n & 1) ret = qmul(ret, a, mod);
            a = qmul(a, a, mod);
            n >>= 1;
        }
        return ret;
    }
    bool check(LL p) {
        if (p < 2) return 0;
        if (p != 2 && p % 2 == 0) return 0;
        LL s = p - 1;
        while (!(s & 1)) s >>= 1;
        for (int i = 0; i < 5; ++i) {
            if (p == prime[i]) return 1;
            LL t = s, m = qpow(prime[i], s, p);
            while (t != p - 1 && m != 1 && m != p - 1) {
                m = qmul(m, m, p);
                t <<= 1;
            }
            if (m != p - 1 && !(t & 1)) return 0;
        }
        return 1;
    }
}Mi;

唯一分解定理

唯一分解定理，也叫算术基本定理，指的是任意n>=2,都可以分解为

其中为质数。
其包括两个断言：
断言1：数n可以以某种方式分解成素数乘积。
断言2：仅有一种这样的因数分解。（除因数排重外）
其可化简为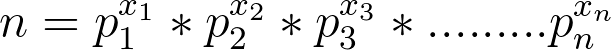
实现方法1：

#include 
#define maxn 10005
using namespace std;
int main()
{

    int n,i=0;
    int cnt=0;
    int a[maxn]={0};//存储其所有因子
    scanf("%d",&n);
    for(i=2;i<=n;i++)
    {
        while(n%i==0)
        {
            a[cnt++]=i;
            n/=i;
        }
    }
    for(i=0;i

实现方法2：

我们要的其实是n的所有素数因子，所以我们只要预先用欧拉筛打个素数表，遍历的时候就只用遍历素数了，这样可以快一点，并且可以处理1e12以内的数。

#include 
typedef long long ll;
using namespace std;
int prime[10000005];
int a[1000005];
bool vis[10000005];
int cnt=0;
void primejudge(int n)
{
    memset(vis,false,sizeof(vis));
    vis[1]=true;
    int i,j;
    for(i=2;i<=n;i++)
    {
        if(!vis[i]) prime[cnt++]=i;
        for(j=0;j

应用1:计算因子有多少个。设f(x)表示x的因子数，则f(a)=(1+x1)(1+x2)(1+x3)…(1+xn)，将上代码改造一下，就可以求得f(a).

同余

如果m整除a-b，我们就说a与b模m同余，并记之为 ，例如 我们有
若 ，则有
若 ，则
若 ，则
注意：用数除同余式并非总是可能的，换句话说 并不能得出

逆元

逆元的定义（摘自离散数学课本）：设一个代数系统 ，这里是定义在A上的一个二元运算，e是A中关于运算的幺元。如果对于A中的每个元素a存在着A中的某个元素b，使得ba=e，那么称b为a的左逆元，如果ab=e成立，那么称b为a的右逆元，如果一个元素b，它既是a的左逆元又是a的右逆元，那么称b是a的一个逆元。
我们在ACM中只需要了解这个：如果p是一个质数，a<=p,如果
那么x就是a的逆元，记作
这样定义后 ，也就是我们把除法转换成了乘法
计算逆元？

• 方法1：费马小定理
  定理内容：设p是素数，a是任意整数且 ，则
  如何用它求逆元？
  ，则 ，即
  可以使用快速幂求解
  快速幂的代码实现

ll qpow(ll k,ll n,ll mod)
{
    ll ans=1;
    while(n>0)
    {
        if(n%2!=0) ans=ans*k%mod;
        k=k*k%mod;
        n/=2; 
    }
    return ans;
}
ll inv(ll n,ll mod)
{
    return qpow(n,mod-2,mod);
}

欧拉函数

欧拉函数是小于x的整数中与x互质的数的个数，一般用φ(x)表示。特殊的，φ(1)=1。
性质：
（1）欧拉公式：若gcd(a,m)=1（最大公约数）,则
（2）若n是素数，则
（3）

• 方法2：扩展欧几里得定理
  欧几里得有个非常强的定理，即gcd(a,b)=gcd(b,a mod b)。
  扩展欧几里得算法的功能就更强大了，它可以用来求二元一次方程的通解，即ax+by=c的通解，还可以用来求乘法逆元。
  若有 ax ≡ 1 （mod m），则称 x 为a关于m的乘法逆元，等价式 a * x+m * y = 1
  这就也是个二元一次方程了，可以用扩展欧几里得算法实现。扩展欧几里得算法的功能就更强大了，它可以用来求二元一次方程的通解，还可以用来求乘法逆元。
  在此顺便简介一下乘法逆元：
  若有 ax ≡ 1 （mod m），则称 x 为a关于m的乘法逆元，等价式 a * x+m * y = 1
  这就也是个二元一次方程了，ExGcd可搞。

设二元一次方程为a * x+b * y=c ，则该方程有解的条件是gcd(a,b)|c
我们先考虑a * x+b * y=gcd(a,b) 的情况，当b=0时,gcd(a,b)=a，此时有等式a*x=a，则此时x=1，设y=0。
设a * x1+b * y1=gcd(a,b),b * x2+(a%b) * y2=gcd(b,a%b) ，则由于有gcd(a,b)=gcd(b,a%b)
，有 a * x1+b * y1=b * x2+(a%b)*y2 ，又由于有
，带入整理
则得到迭代做法：

扩展欧几里得算法及证明

中国剩余定理

浅谈中国剩余定理
我们先来看这样一道题目：

树王种了一棵treap，她现在决定把这棵treap改造为一棵无旋多叉triep，于是她摘下了treap的所有节点，发现如果她把节点3个3个一打包，会剩下2个节点。如果她把节点5个5个一打包，会剩下3个节点，如果把节点7个7个一打包，会剩下2个节点，求这棵treap最少有多少节点？

简化后题目就是，已知x%3=2,x%5=3,x%7=2，求x最小值？

如何解决呢？我们设k1,k2,k3满足 k1%3=1,k1%5=0,k1%7=0,k2%5=1,k2%3=0,k2%7=0.k3%7=1.,k3%3=0,k3%5=0.

那么 k12+k23+k3*2一定是满足答案的一个解。（网上说容易意会，容易意会个鬼啊）

证明： 设x=k1 * 2+k2 * 3+k3 * 2。 则x%3=(k1 * 2+k2 * 3+k3 * 2)%3=(k1 * 2%3+k2 * 3%3+k3 * 2%3)%3=(2+0+0)%3=2;

其他两组解同理。

那么如何求k1,k2,k3？

我们求出LCM（3,5,7）=105,设x1=LCM(3,5,7)/3=35,x2=LCM(3,5,7)/5=21,x3==LCM(3,5,7)/7=15.

那么设k1=n1 * x1,k2=n2 * x2,k3=n3 * x3.

k1%3=1,k2%5=1,k3%7=3,可转换为 n1 * x1%3=1,n2 * x2%5=1,n3 * x3%7=1.

然后可以用扩展欧几里得求出n1,n2,n3.进而得到 k1,k2,k3.

最后便可得到答案，而题目的通解可表示为这个数每次都加上3,5,7的最小公倍数。

好了，现在步入正题（你没看错现在我才开始讲正经的，刚才那一堆都是铺垫）

已知 x≡a1y[1],x≡a2y[2],x≡a3y[3]…x≡any[n].

其中 y[1],y[2],y[3]…y[n]两两互质，求x

其算法流程如下。

1.计算LCM（y1,y2…yn）。

2.从1->n，计算f[i]=LCM(y[1[,y[2],…y[n])/y[i].

3.使用扩展欧几里得定理,对同余式b[i]*f[i]%y[i]=1，计算出b[i]，进而得出k[i]=b[i]*f[i].

4.从1->n,计算x=k[1]*a[1]+k[2]*a[2]+…k[n]*a[n].

5.对x模lcm，得到答案。

接下来给出代码：

#include 
#define maxn 105
using namespace std;
int ex_gcd(int a,int b,int &x,int &y)//扩展欧几里得定理，解ax+by=c。
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int ans=ex_gcd(b,a%b,x,y);
    int temp=x;
    x=y;
    y=temp-(a/b)*x;
    return ans;
}
int a[maxn],b[maxn],n,f[maxn];
int solve()
{
    int ans=0;
    int lcm=1;
    for(int i=1;i<=n;i++)
    {
        lcm*=a[i];//两两互质，直接乘了
    }
    for(int i=1;i<=n;i++)
    {
        f[i]=lcm/a[i];
    }
    for(int i=1;i<=n;i++)
    {
        int x,y,g;
        g=ex_gcd(f[i],a[i],x,y);
        x=(x%a[i]+a[i])%a[i];//因为扩展欧几里得求出的解可能有很多组，且可能为负，我们这步求出了一个比a[i]小且大于0的解。
        ans=(ans+x*f[i]*b[i])%lcm;
    }
    return ans;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&a[i],&b[i]);//ans%a[i]=b[i].
    }
    int ans=solve();
    printf("%d\n",ans);
}

接下来我们谈谈扩展中国剩余定理

今天才被扩展欧拉定理gank的我来学习扩展中国剩余定理了

已知 x≡a1y[1],x≡a2y[2],x≡a3y[3]…x≡any[n]，求x。

现在y[1],y[2]…y[n]不互质了，一般情况的中国剩余定理不适用了，这怎么搞？

考虑 两个方程，分别为x≡a1y[1],x≡a2y[2].

则有x=y[1]*n1+a[1],x=y[2]*n2+a[2].

合并得 y[1]*n1+a[1]=y[2]*n2+a[2].化简: y[1]*n1-y[2]*n2=a[2]-a[1].

使用扩展欧几里得定理 解除最小正整数解 n1，设k=y[1]*n1+a[1].

那么存在通解x=k+t*lcm(y[1],y[2]).有 x≡k(mod)lcm(y[1],y[2])。

一路合并下去就ok了。

接下来给出例题 POJ2891代码

传送门：Strange Way to Express Integers

#include 
#define maxn 100005
using namespace std;
typedef long long ll;
ll ex_gcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得定理，解ax+by=c。
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ll ans=ex_gcd(b,a%b,x,y);
    ll temp=x;
    x=y;
    y=temp-(a/b)*x;
    return ans;
}
ll a[maxn],b[maxn],n,f[maxn];
ll China()
{
    ll mod=a[1],reminder=b[1];//模数为mod,余数为reminder。
    for(int i=2;i<=n;i++)
    {
        ll x,y,g,temp;
        g=ex_gcd(mod,a[i],x,y);
        temp=b[i]-reminder;
        if(temp%g!=0)
        {
            return -1;
        }
        x=x*temp/g;
        ll t=a[i]/g;
        x=(x%t+t)%t;
        reminder=x*mod+reminder;
        mod=mod/g*a[i];
        reminder%=mod;
    }
    reminder=(reminder%mod+mod)%mod;
    return reminder;
}
int main()
{
    while(~scanf("%lld",&n))
    {
        for(ll i=1;i<=n;i++)
        {
            scanf("%lld%lld",&a[i],&b[i]);
        }
        printf("%lld\n",China());
    }
}