数学建模笔记_层次分析法及matlab实现代码（1）

太长不看版（重点总结）：

层次分析法的步骤：

（1） 建立“目标层”“准则层”“方案层”的层级结构。用图示法将层级结构表示出来。
（2） 按照层级结构构造判断矩阵。
（3） 将判断矩阵进行一致性检验，而后计算相对权重。计算相对权重时可以三种方法都用一遍，分别得出方案后进行比较

层次分析法的局限性：

（1）目标层不能太多，因为如果n值过大，就没有RI的数据了。
（2）目标层的指标如果有给定的数据则不能使用层次分析法。

---

通过一个例子引出层次分析法

例：小明想去苏杭、北戴河、桂林三个中的一个地方去旅游，请确定评价指标，形成评价体系选择最优方案。

首先，按照“目标层”“决策层”“方案层”的结构，提出三个问题：

①我们评价的目标是什么？答：为小明同学选择最佳的旅游景点。
②我们为了达到这个目标有哪几种可选的方案？ 答：三种，分别是去苏杭、去北戴河和去桂林。
③评价的准则或者说指标是什么？（我们根据什么东西来评价好坏） 答：景色、花费、居住、饮食、交通。

一次性考虑这五个指标之间的关系，往往考虑不周。所以应该先确定五个指标的权重。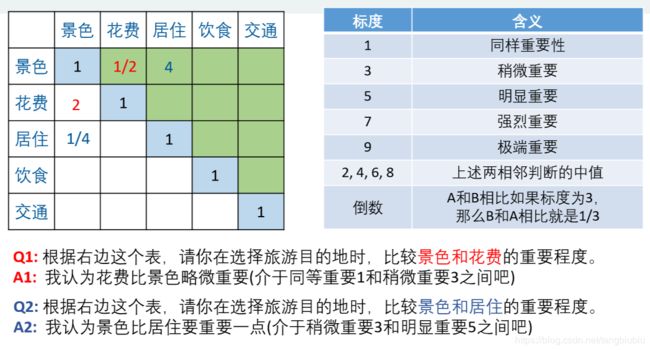
填好的这张表我们看作一个5×5的矩阵A，对应元素为a_ij
（1）a_ij表示：与j相比i的重要程度。
（2）a_i>0且a_ij×a_ji=1（这样的矩阵成为“正互反矩阵”）
这样的矩阵就是层次分析法中的判断矩阵。

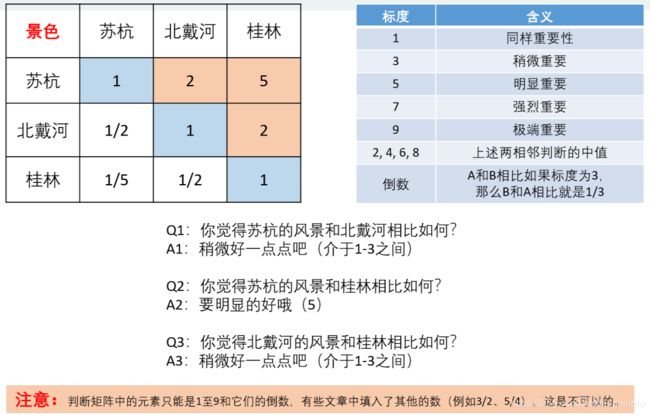
按照上图的标准，花费、居住、饮食、交通分别也填写相应的判断矩阵。

注意：判断矩阵有可能会出现互相矛盾的问题，如下图：
实际上，判断矩阵对角线上的“1”可看作是这一行的标准A，也就是说，这一行的其他元素都是与标准A相比的权重。A与自己相比，权重自然应该是1。一旦某一行的完全确定以后，其他的行只是将标准换做其他的元素，但相对的权重关系不应该发生变化，所以每行的元素应该是成比例的。我们可以看到上图中的行与行之间不成比例，才会发生不一致的现象。

判断矩阵要想不出现矛盾，就必须进行一致性检验。
一致矩阵的特点：各行各列都是成比例的。

正互反n阶矩阵A为一致矩阵时，最大特征值λ_max=n；非一致矩阵的最大特征值λ_max>n。

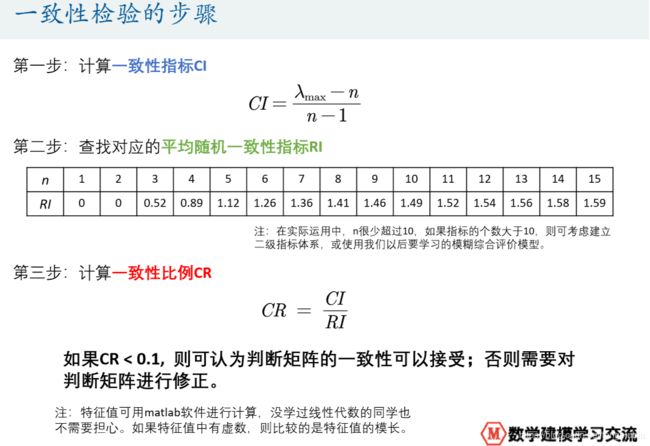经过一致性检验的判断矩阵就可以计算权重了。权重需要进行归一化处理。如果判断矩阵经过了检验，但不是严格的一致矩阵，则先用各行的数据计算权重，进行归一化之后计算平均权重。
计算平均权重有三种方式：
（1） 计算各行的算数平均数
（2） 计算各行的几何平均数
（3） 特征值法求权重。
在比赛中用三种方法都算一遍，分别得出方案，在进行分析。保证了结果的稳健性。

最后，将各个指标的权重全部放入总的判断矩阵中。计算出每个方案的总得分。如下图。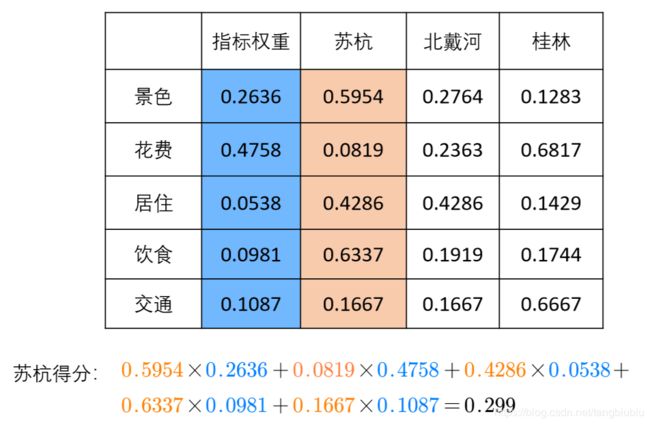如上图这样计算，我们就得出了苏杭的得分。最后，分别算出每个方案的得分进行比较就可以得出最优方案了。

以下是对判断矩阵分析的matlab实现代码：

% 对判断矩阵进行一致性检验，而后计算权重。

a = input("请输入判断矩阵："); % a为判断矩阵
[n,l] = size(a); % n为矩阵的维数

验证正互反矩阵
for i = 1:n 
    for j = 1:n
        if a(i,j)*a(j,i) == 1
            zhenghufan = true;
        else
            zhenghufan = false;
        end
    end
end

if min(min(a)) > 0 && zhenghufan == true 
    disp("判断矩阵为正互反矩阵。");
    GoOn = true;
else
    disp("判断矩阵不是正互反矩阵。")
    GoOn = false;
end

一致性检验
if GoOn
    

    RI_all = [0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];

    [v,d] = eig(a);% v为a特征向量，d为a的特征值对角矩阵


    if rank(a) ~= 1 % 如果判断矩阵不是一致性矩阵，则进行一致性检验。
        disp("进行一致性检验：");
        CI = (max(max(d))-n)/(n-1);
        CI
        RI = RI_all(n); % 查找对应的RI
        RI
        CR = CI/RI
        CR
        if CR < 0.1
        disp("CR<0.10，判断矩阵通过一致性检验。");
        else 
           disp("不通过一致性检验，判断矩阵需要修改。");
           GoOn = false;
        end
    else
        disp("判断矩阵为一致矩阵。")
    end
end

计算权重
%算数平均数权重
if GoOn
    guiyi = zeros(n,n);
    s = 0;
    for i = 1:n
        for j = 1:n
            s = a(i,j)/sum(a(:,j));
            guiyi(i,j) = s;
        end
    end
    
    disp ("判断矩阵算数平均数计算的权重:")
    suanshu = zeros(n,1);
    for i = 1:n
        suanshu(i) = sum(guiyi(i,:))/n;
    end
    suanshu
end

%几何平均数权重
if GoOn
    s = 1;
    xiangcheng = zeros(n,1);
    for i = 1:n
        for j = 1:n
            s = s*a(i,j);
        end
        xiangcheng(i) = s^(1/n);
        s = 1;
    end
    
    jihe = zeros(1,n);
    for i = 1:n
        jihe(i) = xiangcheng(i)/sum(xiangcheng);
    end
    disp ("判断矩阵几何平均数计算的权重:");
    jihe
end

% 特征值法权重

eigenvalue = diag(d);
[M,I] = max(eigenvalue);
disp ("最大特征值为:");
M
disp ("对应的特征向量为:");
v(:,I)
tezheng = zeros(1,n);
    for i = 1:n
        tezheng(i) = v(i,I)/sum(v(:,I));
    end
disp("判断矩阵特征值法的权重为：");
tezheng

学习资源和部分图片来自“清风数学建模”