从零手写VIO(四)
对从零手写VIO第四次作业进行总结
文章目录
- 1 信息矩阵与边缘化
- 1.1 信息矩阵
- 1.2 marg掉ξ1
- 2 BA信息矩阵计算
- 2.1 雅克比计算
- 2.2 H的结构
- 2.3 验证零空间维度
- 2.3.1 零空间问题
- 2.3.2 奇异值分解:
- 2.3.3 对策
作业:

1 信息矩阵与边缘化
1.1 信息矩阵
由图中能够看到,我们的优化变量有6个,分别为ξ1,ξ2,ξ3,L1,L2,L3,误差项有9个,所以雅克比矩阵形式为:
J = ∂ r ∂ ξ = [ ∂ r ( ξ 1 , ξ 2 ) ∂ ξ ∂ r ( ξ 1 , L 1 ) ∂ ξ ∂ r ( ξ 1 , L 2 ) ∂ ξ ∂ r ( ξ 2 , ξ 3 ) ∂ ξ ∂ r ( ξ 2 , L 1 ) ∂ ξ ∂ r ( ξ 2 , L 2 ) ∂ ξ ∂ r ( ξ 2 , L 3 ) ∂ ξ ∂ r ( ξ 3 , L 2 ) ∂ ξ ∂ r ( ξ 3 , L 3 ) ∂ ξ ] \bold { J=\frac{\partial r}{\partial \xi}=\begin{bmatrix} \frac{\partial r(\xi1,\xi 2)}{\partial \xi} \\ \\ \frac{\partial r(\xi1,L_1)}{\partial \xi} \\ \\ \frac{\partial r(\xi1,L_2)}{\partial \xi} \\ \\ \frac{\partial r(\xi2,\xi 3)}{\partial \xi} \\ \\ \frac{\partial r(\xi2,L_1)}{\partial \xi} \\ \\ \frac{\partial r(\xi2,L_2)}{\partial \xi} \\ \\ \frac{\partial r(\xi2,L_3)}{\partial \xi} \\ \\ \frac{\partial r(\xi3,L_2)}{\partial \xi} \\ \\ \frac{\partial r(\xi3,L_3)}{\partial \xi} \\ \\ \end{bmatrix} } J=∂ξ∂r=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂ξ∂r(ξ1,ξ2)∂ξ∂r(ξ1,L1)∂ξ∂r(ξ1,L2)∂ξ∂r(ξ2,ξ3)∂ξ∂r(ξ2,L1)∂ξ∂r(ξ2,L2)∂ξ∂r(ξ2,L3)∂ξ∂r(ξ3,L2)∂ξ∂r(ξ3,L3)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
雅克比矩阵具有稀疏性,拿其中的 J 2 J_2 J2举例
J 2 = ∂ r ( ξ 1 , L 1 ) ∂ ξ = [ ∂ r ( ξ 1 , L 1 ) ∂ ξ 1 ∂ r ( ξ 1 , L 1 ) ∂ ξ 2 ∂ r ( ξ 1 , L 1 ) ∂ ξ 3 ∂ r ( ξ 1 , L 1 ) ∂ L 1 ∂ r ( ξ 1 , L 1 ) ∂ L 2 ∂ r ( ξ 1 , L 1 ) ∂ L 3 ] = [ ∂ r ( ξ 1 , L 1 ) ∂ ξ 1 0 0 ∂ r ( ξ 1 , L 1 ) ∂ L 1 0 0 ] \bold{ J_2=\frac{\partial r(\xi1, L1)}{\partial \xi}=\begin{bmatrix} \frac{\partial r(\xi1,L_1)}{\partial \xi 1}& \frac{\partial r(\xi1,L_1)}{\partial \xi 2}& \frac{\partial r(\xi1,L_1)}{\partial \xi 3}& \frac{\partial r(\xi1,L_1)}{\partial L_1}& \frac{\partial r(\xi1,L_1)}{\partial L_2}& \frac{\partial r(\xi1,L_1)}{\partial L_3} \end{bmatrix} = \begin{bmatrix} \frac{\partial r(\xi1,L_1)}{\partial \xi 1}& 0& 0& \frac{\partial r(\xi1,L_1)}{\partial L_1}& 0& 0 \end{bmatrix} } J2=∂ξ∂r(ξ1,L1)=[∂ξ1∂r(ξ1,L1)∂ξ2∂r(ξ1,L1)∂ξ3∂r(ξ1,L1)∂L1∂r(ξ1,L1)∂L2∂r(ξ1,L1)∂L3∂r(ξ1,L1)]=[∂ξ1∂r(ξ1,L1)00∂L1∂r(ξ1,L1)00]
Λ = J T Σ − 1 J ⏟ H \underbrace{ \Lambda = J^T\varSigma^{-1} J}_{\text{H}} H Λ=JTΣ−1J
很容易就能得到信息矩阵的零项和非零项,
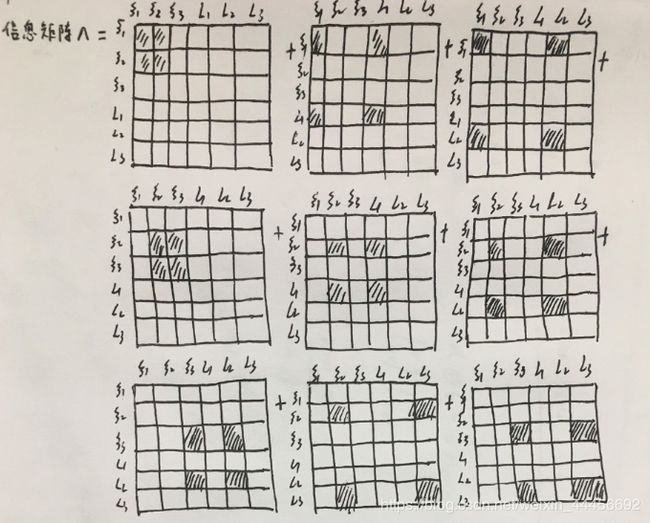
图片参考:https://blog.csdn.net/orange_littlegirl/article/details/103241537
试了几款画图工具,画出来的效果都不是很理想,最后使用MATLAB画出了效果还可以的矩阵块.
对MATLAB有兴趣的可以去看一下matlab绘制矩阵色块图
后记:
后来发现了一种更简单的方法,使用Ubuntu自带的libreOffice Impress也能画出这种图,而且更简单

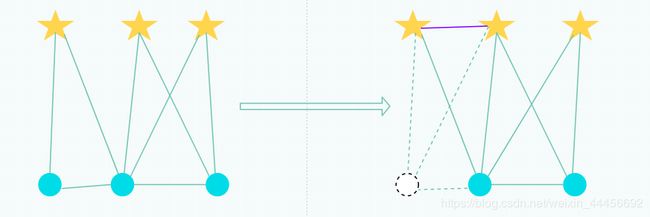
1.2 marg掉ξ1
边缘化 ξ 1 \xi_1 ξ1
边际概率: P a = ∫ P ( a ∣ b ) d b P_a=\int P(a|b)db Pa=∫P(a∣b)db,在这里, b b b就是 ξ 1 \xi_1 ξ1
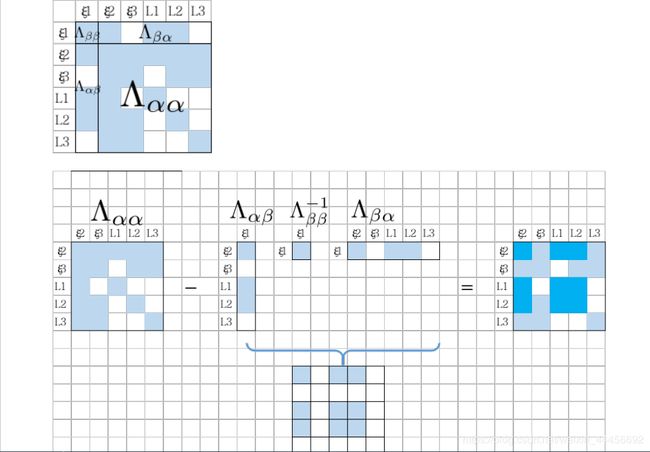
信息矩阵:
Λ = Λ α α − Λ α β Λ β β − 1 Λ β α \Lambda = \Lambda_{\alpha \alpha}-\Lambda_{\alpha \beta}\Lambda_{\beta \beta}^{-1}\Lambda_{\beta \alpha} Λ=Λαα−ΛαβΛββ−1Λβα
其中, Λ = J T Σ − 1 J \Lambda =J^T \varSigma^{-1}J Λ=JTΣ−1J
2 BA信息矩阵计算
2.1 雅克比计算
关于重投影误差雅克比矩阵14讲上有详细的推导过程
重投影误差对相机位姿李代数的导数:
∂ e ∂ δ ξ = − [ f x Z ′ 0 − f x X ′ Z ′ 2 − f x X ′ Y ′ Z ′ 2 f x + f x X 2 Z ′ 2 − f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y − f y Y ′ 2 Z ′ 2 f y X ′ Y ′ Z ′ 2 f y X ′ Z ′ ] \frac{\partial e}{\partial \delta \xi}=-\left[\begin{array}{cccccc} \frac{f_{x}}{Z^{\prime}} & 0 & -\frac{f_{x} X^{\prime}}{Z^{\prime 2}} & -\frac{f_{x} X^{\prime} Y^{\prime}}{Z^{\prime 2}} & f_{x}+\frac{f_{x} X^{2}}{Z^{\prime 2}} & -\frac{f_{x} Y^{\prime}}{Z^{\prime}} \\ 0 & \frac{f_{y}}{Z^{\prime}} & -\frac{f_{y} Y^{\prime}}{Z^{\prime 2}} & -f_{y}-\frac{f_{y} Y^{\prime 2}}{Z^{\prime 2}} & \frac{f_{y} X^{\prime} Y^{\prime}}{Z^{\prime 2}} & \frac{f_{y} X^{\prime}}{Z^{\prime}} \end{array}\right] ∂δξ∂e=−[Z′fx00Z′fy−Z′2fxX′−Z′2fyY′−Z′2fxX′Y′−fy−Z′2fyY′2fx+Z′2fxX2Z′2fyX′Y′−Z′fxY′Z′fyX′]
重投影误差对空间特征点导数:
∂ e ∂ P = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] R \frac{\partial e}{\partial \boldsymbol{P}}=-\left[\begin{array}{ccc} \frac{f_{x}}{Z^{\prime}} & 0 & -\frac{f_{x} X^{\prime}}{Z^{\prime 2}} \\ 0 & \frac{f_{y}}{Z^{\prime}} & -\frac{f_{y} Y^{\prime}}{Z^{\prime 2}} \end{array}\right] R ∂P∂e=−[Z′fx00Z′fy−Z′2fxX′−Z′2fyY′]R
代码实现:
double x = Pc.x();
double y = Pc.y();
double z = Pc.z();
double z_2 = z * z;
Eigen::Matrix<double,2,3> jacobian_uv_Pc;
jacobian_uv_Pc<< fx/z, 0 , -x * fx/z_2,
0, fy/z, -y * fy/z_2;
Eigen::Matrix<double,2,3> jacobian_Pj = jacobian_uv_Pc * Rcw; // 误差关于特征点的导数
Eigen::Matrix<double,2,6> jacobian_Ti;
jacobian_Ti << -x* y * fx/z_2, (1+ x*x/z_2)*fx, -y/z*fx, fx/z, 0 , -x * fx/z_2,
-(1+y*y/z_2)*fy, x*y/z_2 * fy, x/z * fy, 0,fy/z, -y * fy/z_2; // 误差关于相机位姿李代数的导数
2.2 H的结构
图片来源:视觉SLAM十四讲
填充代码:
H.block(i*6,i*6,6,6) += jacobian_Ti.transpose() * jacobian_Ti; //位姿对角线
/// 请补充完整作业信息矩阵块的计算
H.block(j*3 + 6*poseNums,j*3 + 6*poseNums,3,3) += jacobian_Pj.transpose() *jacobian_Pj ; // 空间点对角线
H.block(i*6,j*3 + 6*poseNums, 6,3) += jacobian_Ti.transpose() * jacobian_Pj; // 非对角线
H.block(j*3 + 6*poseNums,i*6 , 3,6) += jacobian_Pj.transpose() * jacobian_Ti;
对于H矩阵的构建的一点理解:
H = J T J H=J^TJ H=JTJ,所以后面H里面的block都是 jacobian_Ti.transpose()*jacobian_Ti 专业的形式。也就是子块的转置在前,而且所有的子块构建的时候都是带转置的部分在前。
关于H的block填充, i , j 坐标的理解:
首先,camera的维度是6,数量为N ;feature的维度是3,数量是M,所以整个H的维度是6×N+3×M;
H对角线上的block是方阵,所以対应每个block的真实位置为:
camera pose:(i*6,i*6)
feature pose:(6*poseNums+j*3,6*poseNums+j*3)
关于block函数的四个参数
* \param startRow the first row in the block
* \param startCol the first column in the block
* \param blockRows the number of rows in the block
* \param blockCols the number of columns in the block
可以看到,前两个参数为子块在大block中的起始行数和列数,后两个参数为子块自身的维度
2.3 验证零空间维度
2.3.1 零空间问题
原因:

滑动窗口算法优化的时候,信息矩阵如公式(49)变成了两部分,且这两部分计算雅克比时的线性化点不同。这可能会导致信息矩阵的零空间发生变化,从而在求解时引入错误信息。
对于 SLAM 系统而言(如单目 VO), 当我们改变状态量时,测量不变意味着损失函数不会改变,更意味着求解最小二乘时对应的信息矩阵 Λ 存在着零空间。

2.3.2 奇异值分解:
Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);
std::cout << svd.singularValues() <<std::endl;
输出结果:

结论:最后7维确实接近于0.表明零空间的维度为7
关于奇异值分解
J = U Σ V T J=U\varSigma V^T J=UΣVT
在Eigen里面:
JacobiSVD<MatrixXd> svd(J, ComputeThinU | ComputeThinV);
U = svd.matrixU();
V = svd.matrixV();
A = svd.singularValues();
2.3.3 对策
First Estimated Jacobian, 即FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致。
这样就能避免零空间退化而使得不可观变量变得可观.
论文推荐: Tue-Cuong Dong-Si and Anastasios I Mourikis. “Consistency analysis for sliding-window visual odometry”. In: 2012IEEE International Conference on Robotics and Automation. IEEE. 2012, pp. 5202–5209
参考手写VIO学习总结(四)