游戏《孢子》的思考 —— Marching Cube算法
这篇博客介绍了Marching Cube这种用于三角化各类隐式曲面的算法,以及记录了我对应的思考。
背景
游戏《孢子》运用的三角化隐式曲面的算法是Compact Cube算法,然而Compact Cube算法是基于Marching Cube进行的优化算法,所以了解对应的Marching Cube算法是必要的。
Marching Cube算法介绍
总体的Marching Cube算法可以分成两块,一块是根据曲面方程构建出对应的三角形顶点,另一块是构建出对应的点法线。
体素及各顶点的density
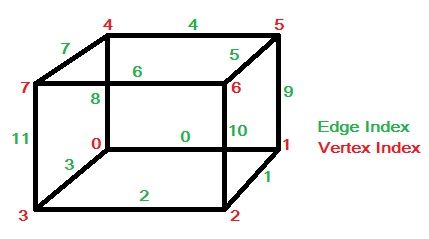
如果想要使用Marching Cube算法来构建对应的三角面的话,那么需要使用到体素。
可以想象,针对于一个球面方程:
在对应的空间中可以散布很多的小立方体栅格。
每个立方体栅格的每个顶点都有对应的Density,根据集合关系可以很方便的推断出:
- 如果一个立方体栅格的每个顶点的Density值都 <0 ,那么可以认为这个立方体完全位于曲面的一侧。
- 同样的,如果每个顶点的Density值都 > ,那么可以认为这个立方体完全位于曲面的另一侧。
- 如果有部分顶点值 <0 ,同时有部分顶点值 >0 ,那么整个曲面与这个立方体相交。此时,通过分析各个顶点的Density值,在对应的边上进行线性插值找到对应的顶点位置,从而构建出这个立方体对应的三角形集。
构建三角形顶点
如果判定立方体栅格与曲面相交,那么根据Density的值正负,每个点有两种可能,因此所有可能数量为 28=256 。
但是,由于数值正负的二元对称性,可以发现如果将对应的正值转负,负值转正,最终产生的结果相同,因此首先可以将其压缩为128种可能数量。
其次,由于各个点的旋转对称性,又可以将这128种可能数量压缩至15种,如下图:
对于情况0来说,由于所有的点的Density值都大于(或小于)0,因此没有三角形产生。而对于剩下的其他情况,都会产生一系列的三角形集。这样一来,就可以构建出对应的三角形顶点了。
计算点法线
点法线的计算也是使用同样的方法来计算 —— 只要取得对应这条边上两个顶点的法线向量,然后进行法线的插值也就可以了。
至于如何取得顶点的法向量呢?比较常用的方法是用Central-Difference Formulas,也就是取得相邻两个顶点的Density在某个方向梯度,从而获取对应的法向量。
具体的公式为:
将梯度向量归一化,就可以获得这个顶点的近似法向量了。
于是,我们只需要针对空间中的这些栅格进行一次这样的操作,就可以构建出我们想要的曲面网格了。
Lookup Table预构建
上面有提到过每个立方体都有256种情况,实际上这个数量也并不太过分,可以将其进行预计算存起来,到时候可以直接进行查找,这样一来就可以很快的输出对应的三角面。
每个顶点都只有两种情况,因此可以使用一个位来进行存储,这样一来就是一个byte……
代码过长并且是纯数据,这里不放出来,可以查看对应的代码块,传送门。
思考
Marching Cube算法看起来很直观,并且实现起来似乎也不难,但是似乎还是有一些值得注意的地方:
连结原本分离的曲面
针对与隐式曲面方程:
这是两个圆心位于 (±1,0,0) ,半径略小于1的圆。这两个圆在原点极为接近。
考虑一个位于原点附近的栅格,有可能同时与两个圆相交,从而构建出的模型可能将这两个模型连结起来,如图:
三角化质量
使用Marching Cube算法,有可能产生一些低质量的三角形。
例如在15种模式中,考虑模式1的三个点都很接近,则会产生很小的三角面。
再考虑模式2,也有可能会产生很细长的三角面。
这些都会降低最后的三角化的质量,因此可以采取一些措施来进行改善。
Compact Cubes就是可行的方案之一。
<全文完>