快速排序分治算法解析

快速排序分治算法解析

声明

文章均为本人技术笔记，转载请注明出处：https://segmentfault.com/u/yzwall

1.快速排序-分治算法思路

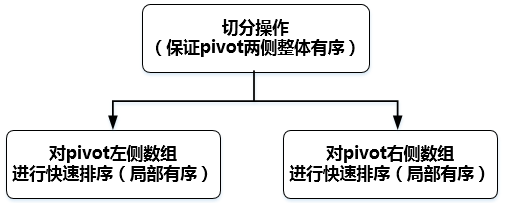
复杂度分析：由于切分算法性能不稳定，快排最差时间复杂度为$O(n ^ 2)$，平均时间复杂度为$O(nlog(n))$，空间复杂度为$O(1)$；

2. 快速排序-划分算法(Partition)

需要升序排序条件下，对于一个轴点$pivot$，一次切分操作完成后保证：

$<= pivot$的都在$pivot$左边，$>= pivot$的都在$pivot$右边

反之，在降序排序条件下，保证

$>= pivot的都在$pivot$左边, $<= pivot$的都在$pivot$右边

2.1 快速排序不稳定性

快速排序的不稳定性在于轴点$pivot$的选择上，如果$pivot$选择数组一边，排序退化为冒泡排序($O(n^2)$)，因此$pivot$尽量选择均匀，通常进行二者取中：
$$
pivot = nums[start + (end - start) / 2]
$$

2.2 leftIndex <= rightIndex辨析

while (leftIndex <= rightIndex) {
    // 在左侧寻找不合法数， A[leftIndex] < pivot，保证切分均匀
    while (leftIndex <= rightIndex && A[leftIndex] < pivot) {
        ...
    }
    
    // 在右侧寻找不合法数， A[rightIndex] > pivot，保证切分均匀
    while (leftIndex <= rightIndex && A[rightIndex] > pivot) {
        ...
    }
    
    // 找到不合法数，将不合法数放入对应区间内
    if (leftIndex <= rightIndex) {
        ...
    }
    quickSort(A, start, rightIndex);
    quickSort(A, leftIndex, end);
}

leftIndex <= rightIndex操作保证分治快排时，分治子数组没有重叠部分，因此如果将
leftIndex <= rightIndex改成leftIndex < rightIndex，递归找不到出口，造成StackOverFlow
当划分操作完成后，必然有：
$$
rightIndex < leftIndexnums
$$

$$
nums[rightIndex] <= nums[leftIndex]
$$

2.3 保证$pivot$切分均匀

// 在左侧寻找不合法数， A[leftIndex] < pivot，保证切分均匀
while (leftIndex <= rightIndex && A[leftIndex] < pivot) {
     leftIndex++;
}

// 在右侧寻找不合法数， A[rightIndex] > pivot，保证切分均匀
while (leftIndex <= rightIndex && A[rightIndex] > pivot) {
    rightIndex--;
}

$=pivot$的数在切分过程中可以放在$pivot$左右两边：为了防止当$=pivot$在数组中大量出现时，如果严格保证$=pivot$的数在$pivot$某一侧，会造成$pivot$选择不均匀，因此必须保证$=pivot$的数字尽量在$pivot$两侧均匀分布，因此整体有序的判断条件为A[leftIndex] < pivot和A[rightIndex] > pivot；

2. 快速排序-分治法递归实现代码

/**
 * http://www.lintcode.com/en/problem/sort-integers-ii/
 * 快速排序一个数组（升序）
 * @author yzwall
 */
class Solution {
    
    public void sortIntegers2(int[] A) {
        if (A == null || A.length == 0) {
            return;
        }
        quickSort(A, 0, A.length - 1);
    }
    
    private void quickSort(int[]A, int start, int end) {
        //　递归出口　单元素不做排序
        if (start >= end) {
            return;
        }
        
        // 切分操作时间复杂度O(n)，空间复杂度O(1)
        int leftIndex = start;
        int rightIndex = end;
        int pivot = A[start + (end - start) / 2];
        
        // leftIndex <= rightIndex, < 导致栈溢出
        while (leftIndex <= rightIndex) {
            // 在左侧寻找不合法数， A[leftIndex] < pivot，保证切分均匀
            while (leftIndex <= rightIndex && A[leftIndex] < pivot) {
                leftIndex++;
            }
            
            // 在右侧寻找不合法数， A[rightIndex] > pivot，保证切分均匀
            while (leftIndex <= rightIndex && A[rightIndex] > pivot) {
                rightIndex--;
            }
            
            // 找到不合法数，将不合法数放入对应区间内
            if (leftIndex <= rightIndex) {
                int temp = A[leftIndex];
                A[leftIndex] = A[rightIndex];
                A[rightIndex] = temp;
                // 继续查找不合法数
                leftIndex++;
                rightIndex--;
            }
        }
        
        /**
         * 跳出循环，leftIndex与rightIndex已互换位置
         * 分治时间复杂度O(logn), 空间复杂度O(1)
         */
        quickSort(A, start, rightIndex);
        quickSort(A, leftIndex, end);
    }
}