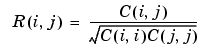MATLAB 协方差 [cov] 和相关系数 [corrcoef] 说明

A,B为两个长度相同的向量

求协方差

S=cov(A,B);

b和c数值上是相等的。

求相关系数

R=corrcoef(A,B)

数值上,f和g是相同到。

相关系数存在许多种类，上述corrcoef 指 pearson correlation coefficient。

---

扩展阅读 1

【copy from:  https://www.cnblogs.com/sanshanyin/p/5397091.html】

协方差

二维随机变量（X，Y），X与Y之间的协方差定义为：

Cov(X,Y)=E{[X-E(X)][Y-E(Y)]}

其中：E(X)为分量X的期望，E(Y)为分量Y的期望

协方差Cov(X,Y)是描述随机变量相互关联程度的一个特征数。从协方差的定义可以看出，它是X的偏差【X-E(X)】与Y的偏差【Y-E(Y)】的乘积的数学期望。由于偏差可正可负，因此协方差也可正可负。

l  当协方差Cov(X,Y)>0时，称X与Y正相关

l  当协方差Cov(X,Y)<0时，称X与Y负相关

l  当协方差Cov(X,Y)=0时，称X与Y不相关

 

举个例子

二维随机变量（身高X，体重Y）（数据是自己编的）

	身高X（cm）	体重Y（500g）	X-E(X)	Y-E(Y)	[X-E(X)][Y-E(Y)]
1	152	92	-19.4	-39.7	770.18
2	185	162	13.6	30.3	412.08
3	169	125	-2.4	-6.7	16.08
4	172	118	0.6	-13.7	-8.22
5	174	122	2.6	-9.7	-25.22
6	168	135	-3.4	3.3	-11.22
7	180	168	8.6	36.3	312.18
	E(X) =171.4	E(Y) =131.7			E{[X-E(X)][Y-E(Y)]}=209.4

根据直觉我们也会想到，身高和体重是有正相关性的，身高较高的体重一般会比较大，同样体重大的身高一般也比较高。计算出来的结果也非常符合我们的直觉。

 

 

再来举一个反例

二维随机变量（玩游戏的时间X，学习成绩Y）（数据是自己编的）

	游戏时间X（h/天）	学习成绩Y	X-E(X)	Y-E(Y)	[X-E(X)][Y-E(Y)]
1	0	95	-1.36	20.7	-28.152
2	1	65	-0.36	-9.3	3.348
3	3	70	1.64	-4.3	-7.052
4	2	55	0.64	-19.3	-12.352
5	2.5	65	1.14	-9.3	-10.602
6	0.5	80	-0.86	5.7	-4.902
7	0.5	90	-0.86	15.7	-13.502
	E(X) =1.36	E(Y) =74.3			E{[X-E(X)][Y-E(Y)]}= -10.5

同样根据直觉我们也会觉得，小朋友玩游戏的时间越长，学习成绩越差的可能性就越大，计算结果也很好的符合我们的直觉。

 

 

从上面两幅散点图上大约可以看出体重随身高的变化趋势，以及学习成绩随玩游戏时间长短的变化趋势。因此，可以说协方差是两个随机变量具有相同变化趋势的度量。

但是，协方差仅能进行定性的分析，并不能进行定量的分析，比如身高体重之间的协方差为209.1，它们之间的相关性具体有多大呢，协方差并没有给出定量的判断标准。因此我们引出相关系数的概念。

相关系数

相关系数的定义

 

其中：Var(X)为X的方差，Var(Y)为Y的方差。

根据施瓦茨不等式可以得到-1

 

l  Corr(X,Y)=1的时候，说明两个随机变量完全正相关，即满足Y=aX+b，a>0

考虑Corr(X,X)，两个随机变量相同，肯定满足线性关系，此时，Cov(X,X)=Var(X)，容易得到Corr(X,Y)=1

l  Corr(X,Y)=-1的时候，说明两个随机变量完全负相关，即满足Y=-aX+b，a>0

l  0<| Corr(X,Y)|<1的时候，说明两个随机变量具有一定程度的线性关系。

还是以前面的两个例子为例，

身高体重：Corr(X,Y)= 209.4/(10.2*24.4)=0.84

游戏时间与学习成绩：Corr(X,Y)= -10.5/(1.1*13.4)= -0.71

有了相关系数，我们可以说，身高与体重之间的线性相关性比游戏时间与学习成绩之间的线性相关性更大。

 

补充说明：

Corr(X,Y)为0，表示X与Y不相关，这里的不相关指的是X与Y没有线性关系，但不是没有关系。因此将“相关”理解为“线性相关”也许更恰当一些。

---

扩展阅读2：

【copy from ：http://blog.sina.com.cn/s/blog_4d7c97a00102vdjo.html】

１。向量的方差与协方差矩阵

cov(x) 

求向量x的方差。

cov(x)为一个数值，数值大小计算公式为S(x)。

cov(x,y) 

求向量x与y的协方差矩阵。

cov(x,y)为2*2矩阵，

[S(x) C(x,y);

 C(y,x) S(y);]

２。矩阵协方差矩阵

cov(X) 

求矩阵X的协方差矩阵。diag(cov(X))得到每一个列向量的方差。sqrt(diag(cov(X)))得到每一个列的标准差。

若Ｘ大小为M*N，则cov(X) 大小为N*N的矩阵。cov(X) 的第(i,j)个元素等于X的第i列向量与第j列向量的方差，即C(Xi,Xj)。

cov(X,Y) 

求矩阵X与Y的协方差矩阵。

若X大小为M*N，Y为K*P，则X，Y的大小必须满足M*N=K*P，即X，Y的元素个数相同。

此时，cov(X,Y) 等于cov([X(:) Y(:)])和cov(X(:),Y(:))，即计算两个向量的协方差矩阵，得到的结果为2*2矩阵。

[S(X(:)) C(X(:),Y(:)); 

C(Y(:),X(:)) S(Y(:));]

可知，S(X) =C(X,X).

3。关于归一化的问题

 在上述的S(X),C(X,Y)计算中，采用的归一化参数是1/(N-1) ,其中N是向量中元素的个数。而下面的调用形式采用的归一化参数是1/N。对应的公式如下图所示。

cov(x,1)

求向量x的方差。计算方法如cov(x)，但归一化参数为1/N。

cov(x,y,1)

求向量x与y的协方差矩阵。计算方法如cov(x,y)，但归一化参数为1/N。

 ４。ＰＳ：

为区别对待，

cov(x)又记作cov(x,0)

cov(x,y)又记作cov(x,y,0)

cov(X) 又记作cov(X,0)

cov(X,Y) 又记作cov(x,y,0)

对于归一化参数为1/(N-1)的情况，当N=1时，自动将参数调整为1/N。

---

扩展阅读3

【copy from https://zhidao.baidu.com/question/228880533.html】

想用MATLAB中的corrcoef函数求两个向量的相关系数。

比如A=[1 2 3];B=[5 3 7]; r= corrcoef(A,B)可以求出相关系数是0.5.为什么两个向量的元素都要是3个以上才行？而只有两个元素的向量如A=[1 2];B=[5 3];不管怎么随机的取，相关系数都是1或-1啊？只含两个元素的向量，都一定相关吗？

这是求相关度的结果，对于一般的矩阵X，执行A=corrcoef(X)后，A中每个值的所在行a和列b，反应的是原矩阵X中相应的第a个列向量和第b个列向量的相似程度（即相关系数）。计算公式是：C(1,2)/SQRT(C(1,1)*C(2,2))，其中C表示矩阵[f,g]的协方差矩阵，假设f和g都是列向量（这两个序列的长度必须一样才能参与运算），则得到的（我们感兴趣的部分）是一个数。以默认的A=corrcoef(f,g)为例，输出A是一个二维矩阵（对角元恒为1），我们感兴趣的f和g的相关系数就存放在A(1,2)=A(2,1)上，其值在[-1,1]之间，1表示最大的正相关，-1表示绝对值最大的负相关

>> A=[1 2 3];B=[5 3 7]; r= corrcoef(A,B)

r =

    1.0000    0.5000

    0.5000    1.0000

>> A=[1 2];B=[5 3];

   r= corrcoef(A,B)

r =

    1.0000   -1.0000

   -1.0000    1.0000%%-1是算出来的，不是说二维向量就一定相关，根据图中r和协方差矩阵的关系

cov(A,B)

ans =

    0.5000   -1.0000

   -1.0000    2.0000%%%A和B的协方差矩阵，

那么R（1,2）=C（1,2）/(sqrt（C（1,1）*C（2,2））)=-1，sqrt为开方的意思。

 

向左转|向右转

追问

非常感谢你的回答，真的是太详细了，我都抄在本子上了呵呵。但还是有一点不明白，
“-1是算出来的，不是说二维向量就一定相关，”什么意思？为什么任何两个二维向量计算出来的相关系数都是1或者-1？
你不是说“1表示最大的正相关，-1表示绝对值最大的负相关”吗？那么任何两个二维的向量都具有最大的正（负）相关性吗？相关系数为1，
也就是相关的。我不是学数学的，是做课题的时候发现这个问题不明白。

追答

>> A=[1 0];B=[0 1];%%二维向量，不相关
   cov(A,B)
ans =
    0.5000   -0.5000
   -0.5000    0.5000
A=[1 2];B=[5 10];%%二维向量，相关
   cov(A,B)
ans =
    0.5000    2.5000
    2.5000   12.5000
  正相关是指两列变量变动方向相同，一列变量由大到小或由小到大变化时，另一列变量亦由大到小或由小到大变化。
  负相关是指两列变量变动方向相反，一列变量由大到小或由小到大变化时，另一列变量反而由小到大或由大到小变化。
  matlab 函数corrcoef也是根据上面的概念计算的，关于二维向量计算总得到-1或者1的问题，我仔细看了下，上面的测试两组数据，
可以看出协方差矩阵中sqrt（C（1,1）*C（2,2））=C（1,2）or-C（1,2）。
也就是说不管你怎么换数据sqrt（C（1,1）*C（2,2））=C（1,2）or-C（1,2）这个式子总是成立的，
所以我个人认为是样本数量（向量维数）少或者是这个函数的缺陷。