显式预测控制（Explicit MPC）

显式预测控制是 Bemporad 等人在2002年提出来的一种面向小规模控制命题的快速 MPC 算法。主要思想是通过参数规划的思想，将优化求解的在线计算放到离线进行，从而提高在线计算的速度。本文从理论上对这种算法进行介绍，并用例子进行一些说明，最后会提到该方法的一些局限和改进。

理论推导

下面我们结合 [BMDP02]，[FBD08] 和 [PRW07] 三篇文章的内容简单介绍一下 Explicit MPC 的原理。这里我们考虑一个离散的，线性时不变的状态空间模型：

x(t+1)=Ax(t)+Bu(t)

其中 x(k)∈Rnx 是系统状态， u(k)∈Rnu 是系统输入。 A,B 都是相应的系数矩阵。为简单起见，我们考虑一个从当前状态 x0 调节到原点的调节问题。同时我们要保证输入和状态都满足一定的约束，即

c−≤Cx(t)≤c¯

d−≤Du(t)≤d¯

对任何k∈N都满足。同时 C∈Rnoc×nx 且 D∈Rnic×nu 是常数矩阵， c−,c¯ 和 d−,d¯ 都是常数向量。

然后 MPC 在没周期求解的 QP 命题为：

minu(0),...,u(N−1)x(0),...,x(N)x(N)TPx(N)+∑i=0N−1(x(i)TQx(i)+u(i)TRu(i))

s.t. x(t+1)=Ax(t)+Bu(t)

(x(0) given)

c−≤Cx(t)≤c¯

d−≤Du(t)≤d¯

其中 P∈Rnx×nx ， Q∈Rnx×nx 是半正定矩阵， R∈Rnu×nu 是正定阵。 N∈N 是预测时域长度（和控制时域等长）。 P 是终端惩罚加权阵，可以通过求解无约束系统的一个黎卡提方程来得到。

通过将 x(t)=Atx(0)+∑t−1j=0AjBu(t−1−j) 代入上式进行替换，上面的优化命题可以写成

J(x(0))=12x(0)TYx(0)+minU12UTHU+x(0)TFU

s.t. GU≥W+Ex(0)

这里这里的 x(0) 代表的是当前时刻的状态， Y,H,F,G,W,E 是常数参数。

上面优化命题的 KKT 条件为：

Hu∗+FTx(0)−GTaλ∗a=0

Gau∗=Wa+Eax(0)

λ∗i=0

Giu∗≥Wi+Eix(0)

λ∗a≥0

其中，上标星号的是最优值，下标 a 的表示有效的约束 (active)，下标 i 的表示无效的约束 (inactive)。

按照 Explicit MPC，或者说 mp-MPC 的理论，我们可以由上面的 KKT 条件得到以下的方程组：

[HGa−GTa0][u∗λ∗a]=[0Wa][−FTEa]x(0)

假设上述方程组可解（ Ga 阵行满秩），我们可以得到与状态参数x(0)线性相关的解：

u∗=Kaxx(0)+cu

λ∗a=Laxx(0)+cλ

其中，

cλ=(GaH−1GTa)−1Wa

Lax=(GaH−1GTa)−1(GaH−1FT+Ea)

cu=H−1GTa(GaH−1GTa)−1Wa

Kax=H−1GTa(GaH−1GTa)−1(GaH−1FT+Ea)−H−1FT

其中 Kax，Lax，cu和cλ 都只依赖与有效集 a 和原命题的数据，和参数 x 并没有关系。而这些参数所适用的可行区域（也就是 Explicit MPC 中所谓的关键区域，critical region, CR）是由 KKT 条件中剩下的几个不等式来确定的，如果我们用上面的解替换掉 KKT 条件中不等式的变量，就可以得到：

Laxx(0)+cλ≥0

GiKaxx(0)+(Gicu−Wi−Eix(0))≥0

因为上面的不等式都是关于当前时刻状态 x(0) 的线性不等式，因此可以将整个状态空间内划分为很多个互不重叠的 CR，示意图如下：

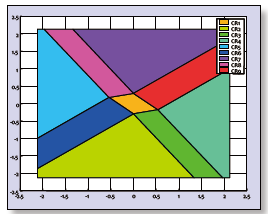
仿真

考虑文章 [BMDP02] 中的一个单入单出的对象：

y(t)=2s2+3s+2u(t)

令采样时间为 0.1s，可以得到其状态空间模型为：

x(t+1)=[0.73260.1722−0.08610.9909]x(t)+[0.06090.0064]u(t)

y(t)=[01.4142]x(t)

状态和输入的约束为：

∥u∥∞≤2,∥x∥∞≤3

因为状态参数是二维的，使得我们可以在平面上画出分区的形状。

当时域长度 N=2 时，大约有10个左右的 CR，状态空间的分区图为：

当时域长度 N=5 时，大约有30个左右的 CR，状态空间的分区图为：

当时域长度 N=10 时，大约有100个左右的 CR，状态空间的分区图为：

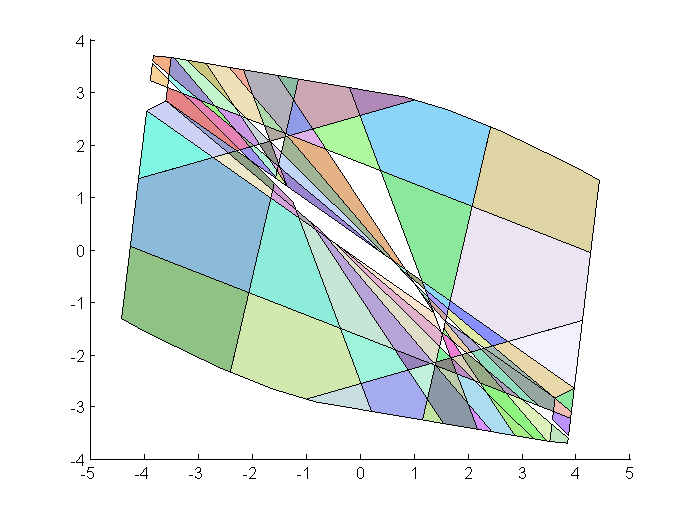
注意：
1 这里分区的形状和数目之所以与文章 [BMDP02] 中不同，是因为约束的选取有所区别，原文中没有对状态 x(t) 的约束。
2 这里分区的数目不是精确的，因为我没有按照原文的算法把每一个分区都计算出来，而是采用随机撒点的方法将撒到的点所在的分区画出来，因为都进行了上千次撒点，因此可以认为我们在这里确定了绝大部分的分区。

局限与改进

在上面的仿真中，我们可以看出来当时域长度增加时，分区数目的上升速度是很可观的，而且这还是最简单的单入单出两状态的对象。因为分区数目和不等式约束的个数有关，即对于 m 个不等式约束，若其中任意 1～m 个约束变为积极约束，那么就可以生成一个 CR， 因此，理论上 m 个不等式约束可以生成 C1m+C2m+...+Cmm 个 CR，其实也就是所有不等式组成的集合的所有子集的个数，即 2m 。而时域长度的增加和问题规模的增大都会使得不等式约束的个数增加。虽然实际上达不到 2m 的规模，但随着问题规模的增大， CR 的个数对与存储空间和在线查找的时间都提出了相当严峻的考验，这也是为什么人们提及 Explicit MPC 时总会说这种方法适用于小规模的问题。

针对 Explicit MPC 的这一缺点，很多人也作了相应的研究。[GTM08] 通过对相同控制律的分区进行归并的方法给出了显示解的一个最小形式。在 [CZJM07] 中用来消除分区的方法是在能保证稳定性的前提下对相邻的分区进行合并。[TJB03] 提出一种方法是采用二叉搜索树来存储状态分区，并在此基础上来计算分段线性函数的值。在此基础上可以实现在 O(logN) 的时间复杂度内实现对根据状态点查找分区的操作。[JG03] 采用的方法是将分区进行近似，然后用正交搜索树来存储各个分区的信息，并在此基础上实现对状态点的定位和线性函数的计算。[BJJ11] 采用的是哈希表对分区信息进行存储。[BF03] 采用的是给出近似解的方法来加快求解的速度。

Ref.
[BMDP02] Bemporad, A., Morari, M., Dua, V., & Pistikopoulos, E. N. (2002). The explicit linear quadratic regulator for constrained systems. Automatica, 38(1), 3-20.
[FBD08] Ferreau, H. J., Bock, H. G., & Diehl, M. (2008). An online active set strategy to overcome the limitations of explicit MPC. International Journal of Robust and Nonlinear Control, 18(8), 816-830.
[PRW07] Pannocchia, G., Rawlings, J. B., & Wright, S. J. (2007). Fast, large-scale model predictive control by partial enumeration. Automatica, 43(5), 852-860.

[BF03] Bemporad A, Filippi C. Suboptimal explicit receding horizon control via approximate multiparametric quadratic programming[J]. Journal of optimization theory and applications, 2003, 117(1): 9-38.
[BJJ11] Bayat, F., Johansen, T. A., & Jalali, A. A. (2011). Using hash tables to manage the time-storage complexity in a point location problem: Application to explicit model predictive control. Automatica, 47(3), 571-577.
[CZJM07] Christophersen, F. J., Zeilinger, M. N., Jones, C. N., & Morari, M. (2007, December). Controller complexity reduction for piecewise affine systems through safe region elimination. In Decision and Control, 2007 46th IEEE Conference on (pp. 4773-4778). IEEE.
[GTM08] Geyer, T., Torrisi, F. D., & Morari, M. (2008). Optimal complexity reduction of polyhedral piecewise affine systems. Automatica, 44(7), 1728-1740.
[JG03] Johansen T A, Grancharova A. Approximate explicit constrained linear model predictive control via orthogonal search tree[J]. Automatic Control, IEEE Transactions on, 2003, 48(5): 810-815.
[TJB03] Tøndel, P., Johansen, T. A., & Bemporad, A. (2003). Evaluation of piecewise affine control via binary search tree. Automatica, 39(5), 945-950.