九、【python计算机视觉编程】图像分割

图像分割在数字图像处理时也提到过，图像分割是将一幅图像分割成有意义区域的过程。 这些区域可以是图像的前景和背景或者图像中一些单独的对象。这些区域可以利用一些诸如颜色、边界或近邻相似性等特征进行构建。

（一）图割（Graph Cut）

图像分割有以下五种分割方法：

1. 基于阈值 的分割方法：
   阈值法的基本思想是基于图像的灰度特征来计算一个或多个灰度阈值，并将图像中每个像素的灰度值与阈值相比较，最后将像素根据比较结果分到合适的类别中。因此，该类方法最为关键的一步就是按照某个准则函数来求解最佳灰度阈值。
2. 基于边缘 的分割方法：
   所谓边缘是指图像中两个不同区域的边界线上连续的像素点的集合，是图像局部特征不连续性的反映，体现了灰度、颜色、纹理等图像特性的突变。通常情况下，基于边缘的分割方法指的是基于灰度值的边缘检测，它是建立在边缘灰度值会呈现出阶跃型或屋顶型变化这一观测基础上的方法。阶跃型边缘两边像素点的灰度值存在着明显的差异，而屋顶型边缘则位于灰度值上升或下降的转折处。
3. 基于区域的分割方法：
   此类方法是将图像按照相似性准则分成不同的区域，主要包括种子区域生长法、区域分裂合并法和分水岭法等几种类型。 种子区域生长法是从一组代表不同生长区域的种子像素开始，接下来将种子像素邻域里符合条件的像素合并到种子像素所代表的生长区域中，并将新添加的像素作为新的种子像素继续合并过程，直到找不到符合条件的新像素为止。该方法的关键是选择合适的初始种子像素以及合理的生长准则。区域分裂合并法（Gonzalez，2002） 的基本思想是首先将图像任意分成若干互不相交的区域，然后再按照相关准则对这些区域进行分裂或者合并从而完成分割任务，该方法既适用于灰度图像分割也适用于纹理图像分割。分水岭法（Meyer，1990） 是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成分水岭。
4. 基于图论的分割方法：
   此类方法把图像分割问题与图的最小割（min cut）问题相关联。分割的最优原则就是使划分后的子图在内部保持相似度最大，而子图之间的相似度保持最小。基于图论的分割方法的本质就是移除特定的边，将图划分为若干子图从而实现分割。
5. 基于能量泛函的分割方法：
   该类方法主要指的是活动轮廓模型（active contour model）以及在其基础上发展出来的算法，其基本思想是使用连续曲线来表达目标边缘，并定义一个能量泛函使得其自变量包括边缘曲线，因此分割过程就转变为求解能量泛函的最小值的过程，一般可通过求解函数对应的欧拉(Euler．Lagrange)方程来实现，能量达到最小时的曲线位置就是目标的轮廓所在。按照模型中曲线表达形式的不同，活动轮廓模型可以分为两大类：参数活动轮廓模型（parametric active contour model）和几何活动轮廓模型（geometric active contour model）。

概念：
Graph cuts是一种十分有用和流行的能量优化算法，在计算机视觉领域普遍应用于前背景分割（Image segmentation）、立体视觉（stereo vision）、抠图（Image matting）等。其基本思想是，相似且彼此相近的像素应该划分到同一区域。

数学原理：
图割$C$（$C$是图中所有边的集合）的“代价”函数定义为所有割的边的权重求合相加：$$E_{cut}=\sum _{(i,j)\in C}{w}_{ij}$$ $w_{ij}$是图中节点$i$到节点$j$的边$（i，j)$的权重，并且是对图割$C$所有的边进行求和。

图割图像分割的思想是用图来表示图像，并对图进行划分以使割代价$E_{cut}$最小。在用图表示图像时，增加两个额外的节点，即源点和汇点；并仅考虑那些将源点和汇点分开的割。

寻找最小割（minimum cut 或min cut）等同于源点和汇点间寻找最大流（maximum flow 或 max flow）。简单理解可以参考以下的过程：

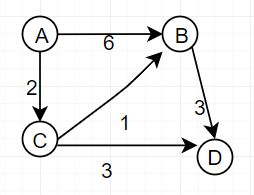
从A到D，中间经过B,C两节点，问此时的最大流是多少？
首先找一条从A到D的路径[A,C,D]，该路径的最大流量是min(2,3)=2，因为[A,C]上面的容量已经被用了，所以路径[A,B,C,D就行不通了，割去[A,C]后图变成了以下形式：

该图叫做残留网络或者残留图，此时再找从A到D的路径[A,B,D]，路径的最大流量是min(3,6)=3.割去[B,D]后，图如下：

此时就不存在从A到D的可行路径了，则结束最大流的查找。此时的最大流是2+3=5，被割的边容量和是2+3=5，即最大流=最小割。

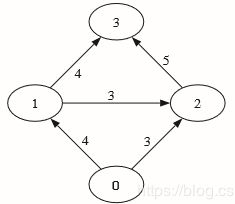
python-graph 工具包计算一幅较小的最大流 / 最小割的示例：

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

gr = digraph()
gr.add_nodes([0,1,2,3])
gr.add_edge((0,1), wt=4)
gr.add_edge((1,2), wt=3)
gr.add_edge((2,3), wt=5)
gr.add_edge((0,2), wt=3)
gr.add_edge((1,3), wt=4)
flows,cuts = maximum_flow(gr, 0, 3)
print ('flow is:' , flows)
print ('cut is:' , cuts)

实验结果如下：

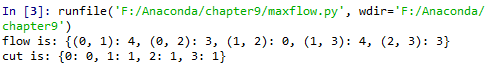
分析：
首先创建有4个节点的有向图，4个节点的索引分别0…3，然后用add_edge()增添边并为每条边指定特定的权重。边的权重用来衡量边的最大流容量。以节点0为源点，3为汇点，计算最大流。

（1）从图像创建图

给定一个邻域结构，可以利用图像像素作为节点定义一个图。在这里讨论最简单的像素四邻域和两个图像区域（前景和背景）的情况。一个四邻域指一个像素与其正上方、正下方、左边、右边的像素直接相连。

除了像素节点外，还需要两个特定的节点——“源”点和 “汇”点，来分别代表图像的前景和背景。

下面给出创建图像中的图像的步骤：

1. 每个像素节点都有一个从源点的传入边
2. 每个像素节点都有一个到汇点的传出边
3. 每个像素节点都有一条传入边和传出边连接到它的近邻

为了确定边的权重，需要一个能够确定这些像素点之间，像素点与源点、汇点之间边的权重（表示那条边的最大流）的分割模型。与前面一样，像素$i$和像素$j$之间的边的权重记为$w_{ij}$，源点到像素$i$的权重记为$w_{si}$，像素$i$到汇点的权重记为$w_{it}$。

假定已经在前景和背景像素（从同一图像或从其他的图像）上训练出一个贝叶斯分类器，就可以为前景和背景计算概率$p_F(I_i)$和$p_B(I_i)$。这里，$I_i$是像素$i$的颜色向量。

现在可以为边的权重建立如下模型：$$w_{si}=\frac{p_F(I_i)}{p_F(I_i)+p_B(I_i)}$$ $$w_{it}=\frac{p_B(I_i)}{p_F(I_i)+p_B(I_i)}$$ $$w_{ij}=k{e}^{-{|I_i-I_j|}^2/\sigma }$$

利用该模型，可以将每个像素和前景及背景（源点和汇点）连接起来，权重等于上面归一化后的概率。$w_{ij}$描述了近邻间像素的相似性，相似像素权重趋近于$k$，不相似的趋近于零。参数$\sigma$表征了随着不相似性的增加，指数次幂衰减到零的快慢。

下面创建一个名为 graphcut.py 的文件，从一幅图像中创建图的函数：

# -*- coding: utf-8 -*-


from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow
import bayes

def build_bayes_graph(im,labels,sigma=1e2,kappa=2):
    """从像素四邻域建立一个图，前景和背景（前景用1标记，背景用-1标记，
    其他的用0标记）由labels决定，并用朴素贝叶斯分类器建模"""
    
    m,n = im.shape[:2]
    
    #每行是一个像素的RGB向量
    vim = im.reshape((-1,3))
    
    #前景和背景(RGB)
    foreground = im[labels==1].reshape((-1,3))
    background = im[labels==-1].reshape((-1,3))
    train_data = [foreground,background]
    
    #训练朴素贝叶斯分类器
    bc = bayes.BayesClassifier()
    bc.train(train_data)
    
    #获取所有像素的概率
    bc_labels,prob = bc.classify(vim)
    prob_fg = prob[0]
    prob_bg = prob[1]
    
    #用m*n+2个节点创建图
    gr = digraph()
    gr.add_node(range(m*n+2))
    source = m*n #倒数第二个是源点
    sink = m*n+1 #最后一个节点是汇点
    
    #归一化
    for i in range(vim.shape[0]):
        vim[i] = vim[i]/linalg.norm(vim[i])
        
    #遍历所有的节点，并添加边
    for i in range(m*n):
        #从源点添加边
        gr.add_edge((source,i),wt=(prob_fg[i]/(prob_fg[i]+prob_bg[i])))
        
    #向汇点添加边
    gr.add_edge((i,sink),wt=(prob_bg[i]/(prob_fg[i]+prob_bg[i])))
    
    #向相邻节点添加边
    if i%n !=0 : #左边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
        gr.add_edge((i,i-1),wt=edge_wt)
    if (i+1)%n !=0 : #右边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+1])**2)/sigma)
        gr.add_edge((i,i+1),wt=edge_wt)
    if i//n !=0 : #上边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-n])**2)/sigma)
        gr.add_edge((i,i-n),wt=edge_wt)
    if i//n !=m-1 : #下左边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i+n])**2)/sigma)
        gr.add_edge((i,i+n),wt=edge_wt)
        
    return gr

在这个函数中，用1标记前景训练数据、用-1标记背景训练数据的一幅标记图像。基于这种标记，在RGB值上可以训练出一个朴素贝叶斯分类器，然后计算每一像素的分类概率，这些计算出的分类概率便是从源点出来和到汇点去的边的权重，由此可以创建一个节点为n*m+2的图。注意源点和汇点的索引，为了简化像素的索引，将最后的两个索引作为源点和汇点的索引。

为了在图像上可视化覆盖的标记区域，可以利用contourf()函数填充图像（这里指带标记图像）等高线间的区域，参数alpha用于设置透明度。图建立起来后便需要在最优位置对图进行分割，cut_graph() 函数可以计算最小割并将输出结果重新格式化为一个带像素标记的二值图像。 添加下面的内容到 graphcut.py 中：

def show_labeling(im,labels):
    """显示图像的前景和背景区域。前景labels=1,背景labels=-1,其他labels=0"""
    
    imshow(im)
    contour(labels,[-0.5,0.5])
    coutourf(labels,[-1,-0.5],colors='b',alpha=0.25)
    coutourf(labels,[0.5,1],colors='r',alpha=0.25)
    axis('off')
    
def cut_graph(gr,imsize):
    """用最大流对图gr进行分割，并返回分割结果的二值标记"""
    
    m,n = imsize
    source = m*n #倒数第二个节点是源点
    sink = m*n+1 #倒数第一个是汇点
    
    #对图进行分割
    flows,cuts = maximun_flow(gr,source,sink)
    
    #将图转为带有标记的图像
    res = zeros(m*n)
    for pos,label in cuts.items()[:-2]: #不要添加源点/汇点
        res[pos] = label
        
    return res.reshape((m,n))

需要再次注意源点和汇点的索引，需要将图像的尺寸作为输入去计算这些索引，在返回分割结果之前要对输出结果进行reshape()操作。割以字典返回，需要将它复制到分割标记图像中，这通过返回列表（键，值）的.iten() 方法完成。

编写实验代码：读取一幅图像，从图像的两个矩形区域估算出类概率，然后创建一个图：

# -*- coding: utf-8 -*-

from scipy.misc import imresize
from PCV.tools import graphcut
from PIL import Image
from numpy import *
from pylab import *

im = array(Image.open("empire.jpg"))
im = imresize(im, 0.07,interp='bilinear')
size = im.shape[:2]
print ("OK!!")
# add two rectangular training regions
labels = zeros(size)
labels[3:18, 3:18] = -1
labels[-18:-3, -18:-3] = 1
print ("OK!!")
# create graph
g = graphcut.build_bayes_graph(im, labels, kappa=2)   #k决定领进像素间的相对权重
 
# cut the graph
res = graphcut.cut_graph(g, size)
print ("OK!!")
figure()
graphcut.show_labeling(im, labels)
figure()
imshow(res)
gray()
axis('off')
show()

实验结果：

下面图二是g = graphcut.build_bayes_graph(im, labels, kappa=1)的kappa的数值为1时的图像。

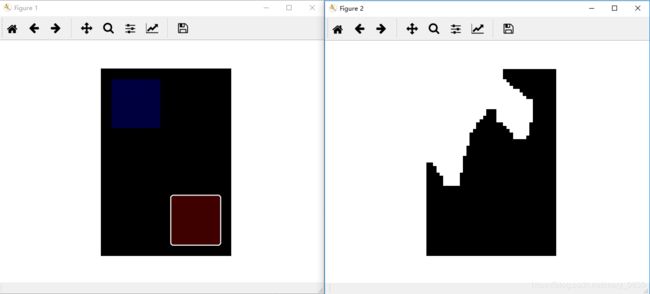
下面图二是g = graphcut.build_bayes_graph(im, labels, kappa=2)的kappa的数值为2时的图像。

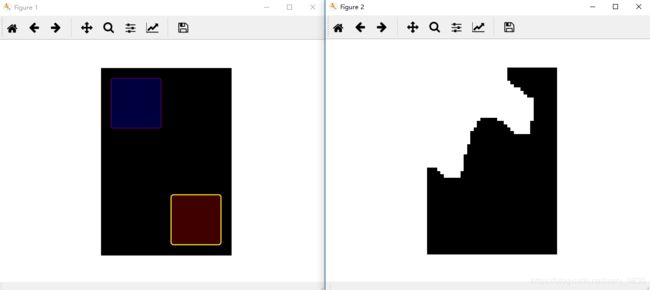
下面图二是g = graphcut.build_bayes_graph(im, labels, kappa=5)的kappa的数值为5时的图像。

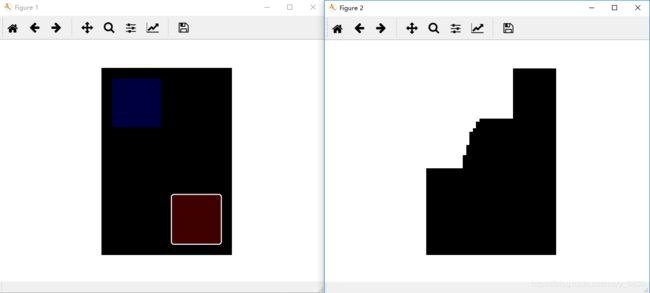
从上面的图可以看出，类概率之间的相对权重对分割结果产生影响。当k越大时，其分割边缘越圆润，图像的细节也逐渐丢失了。这是由于kappa决定了邻近像素间边的相对权重，权重越高，越丢失严重。

遇到的问题及解决方案：

想要注释掉这个包含imresize的语句，意思就是不改变这个图的大小。之后就出现了如下的问题：
z
这个问题就是数据量过大，导致内存不足，需要修改图像的数据量大小，还是回到了原来的问题上。

错误原因：在Python 2.X中, for pos,label in cuts.items()[:-2]: #don’t add source/sink 返回的是一个 list, 但是在Python 3.X中返回的是一个dict_keys object。

修改方式：for pos,label in list(cuts.items())[:-2]:

（2）用户交互式分割

利用一些方法可以将图割分割与用户交互结合起来，形成用户交互式分割。例如，用户可以在一幅图像上为前景和背景提供一些标记。另一种方法就是利用边界框或“lasso”工具选择一个包含前景的区域。

下面给出一个完整的例子。实验会载入一幅图像及对应的标注信息，然后将其传递到我们的图割路径中：

# -*- coding: utf-8 -*-
from scipy.misc import imresize
from PCV.tools import graphcut
from PIL import Image
from numpy import *
from pylab import *

def create_msr_labels(m, lasso=False):
    """ Create label matrix for training from
    user annotations. """
    labels = zeros(im.shape[:2])
    # background
    labels[m == 0] = -1
    labels[m == 64] = -1
    # foreground
    if lasso:
        labels[m == 255] = 1
    else:
        labels[m == 128] = 1
    return labels

# load image and annotation map
im = array(Image.open('empire.jpg'))
m = array(Image.open('empire.bmp'))
# resize
scale = 0.1
im = imresize(im, scale, interp='bilinear')
m = imresize(m, scale, interp='nearest')
# create training labels
labels = create_msr_labels(m, False)
# build graph using annotations
g = graphcut.build_bayes_graph(im, labels, kappa=2)

# cut graph
res = graphcut.cut_graph(g, im.shape[:2])
# remove parts in background
res[m == 0] = 1
res[m == 64] = 1

# plot the result
figure()
imshow(res)
gray()
xticks([])
yticks([])
savefig('labelplot.pdf')

实验结果：

由于遇到的bug没有解决，实验结果没能如愿显示出来，故截取了书上的结果显示如上。待小白博主解决了再修改这部分内容，希望有知道解决这个bug的小伙伴能留言指导我一下，感谢！

更新：
经过多方面的咨询，遇到上面问题的原因可能是标注的图应该需要专业人士标注好的，不能随意生成bmp文件。所以，解决方案就是用专业人士已标注好的数据包进行实验，即可得出实验结果。

修改后的实验结果如下：




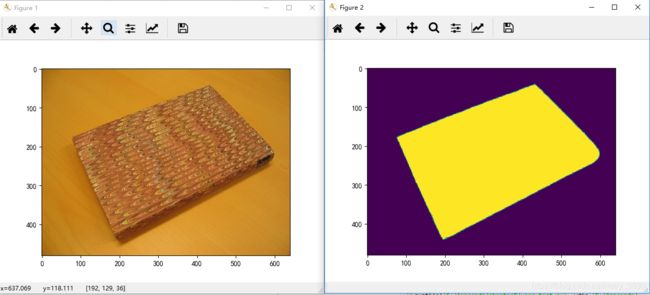
实验说明：
从上面三组实验中可知，前景和背景容易分开的图像中，图像分割得比较好，但是在颜色复杂的图像中，分割效果并没有那么好。正如书本和香蕉那样，前景和背景分割开来，但是在第三组图像中，两个人物的图割则只分割了左边女士脚的部分。而且也发现，虽然简单图像的图割效果比较好，但有些细节的东西并没有能够检测出来并分割开。

遇到的问题：

File “F:/Anaconda/chapter9/user_test.py”, line 15, in create_msr_labels
labels[m==0]=-1
IndexError: too many indices for array

（二）利用聚变进行分割

现在将介绍一种分割图像图的方法，即基于谱图理论的归一化分割算法，它将像素相似和空间近似结合起来对图像进行分割。

原理：
这个方法来自定义一个分割损失函数，该损失函数不仅考虑了组的大小而且还用划分的大小对该损失函数进行“归一化”。该归一化后的分割公式将方程中分割损失函数修改为：$$E_{ncut}=\frac{E_{cut}}{{\sum }_{i\in A}^{}{w}_{ix}}+\frac{E_{cut}}{{\sum }_{j\in B}^{}{w}_{jx}}$$
A和B表示两个割集，并在图中分别对A和B中所有其他节点（函数进行“归一化”这里指图像像素）的权重求和相加，相加求和项称为association。对于那些像素与其他像素具有相同连接数的图像，它是对划分大小的一种粗糙度量方式。

定义$W$为边的权重矩阵，矩阵中的元素$w_{ij}$为连接像素$i$和像素$j$边的权重。$D$为对$W$每行元素求和后构成的对角矩阵，即$D=diag(d_i)，d_i={\sum }_j{w}_{ij}$。归一化分割可以通过最小化下面的优化问题而求得：$$mi{n}_y\frac{y^T(D-W)y}{y^{T}Dy}$$ 向量$y$包含的是离散标记，这些离散标记满足对于$b$为常数$y_i\in \left\{1,-b\right\}$（即$y$只可以取这两个值）的约束，$y^{T}D$求和为0。

通过松弛约束条件并让$y$取任意实数，该问题可以变为一个容易求解的特征分解问题。这样求解的缺点是你需要对输出设定阈值或进行聚类，使它重新成为一个离散分割。

松弛该问题后，该问题便成为求解拉普拉斯矩阵特征向量问题：
$$L=D^{-1/2}W{D}^{-1/2}$$
正如谱聚类情形一样，现在的难点是如何定义像素间边的权重$w_{ij}$。

利用原始归一化割中的边的权重，通过下面的式子给出连接像素$i$和像素$j$的边的权重：$$w_{ij}=e^{-{|I_i-I_j|}^2/{\sigma }_g}{e}^{-{|x_i-x_j|}^2/{\sigma }_d}$$ 公式中第一部分度量像素$I_i$和$I_j$之间的像素相似性，$I_i\left(I_j\right)$定义为RGB向量或灰度值；第二部分度量图像中$x_i$和$x_j$的接近程度，$x_i\left(x_j\right)$定义为每个像素的坐标矢量，缩放因子${\sigma }_d$和${\sigma }_g$ 决定了相对尺度和每一部件趋近0的快慢。

代码实现所述原理：

# -*- coding: utf-8 -*-

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow
import bayes
import numpy
import scipy

def ncut_graph_matrix(im,sigma_d=1e2,sigma_g=1e-2):
    """创建用于归一化割的矩阵，其中sigma_d和sigma_g是像素距离和像素相似性的权重参数"""
    
    m,n = im.shape[:2]
    N = m*n
    
    #归一化，并创建RGB或灰度特征向量
    if len(im.shape)==3:
        for i in range(3):
            im[:,:,i] = im[:,:,i] / im[:,:,i].max()
        vim = im.reshape((-1,3))
    else:
        im = im / im.max()
        vim = im.flatten()
        
    #x,y坐标用于距离计算
    xx,yy = meshgrid(range(n),range(m))
    x,y = xx.flatten(),yy.flatten()
    
    #创建边线权重矩阵
    W = zeros((N,N),'f')
    for i in range(N):
        for j in range(i,N):
            d = (x[i]-x[j])**2+(y[i]-y[j])**2
            W[i,j] = W[j,i] = exp(-1.0*sum((vim[i]-vim[j])**2)/sigma_g)*exp(-d/sigma_d)
    return W

这个函数获取图像数组，并利用输入的彩色图像RGB值或灰度图像的灰度值创建一个特征向量。由于边的权重包含了距离部件，对于每个像素的特征向量，利用meshgrid()函数来获取$x$和$y$的值，然后该函数会在$N$个像素数上循环，并在$N\times N$归一化割矩阵W中填充值。

可以顺序分割每个特征向量或获取一些特征向量对它们进行聚类来计算分割结果。这里选择第二种方法，它不需要修改任意分割数也能正常工作。将拉普拉斯矩阵进行特征分解后的前ndim个特征向量合并在一起构成矩阵$W$，并对这些像素进行聚类。下面函数实现了这种聚类过程：

# -*- coding: utf-8 -*-
from numpy import *
from PIL import Image
from PCV.tools import graphcut
import ncut
from scipy.misc import imresize
from pylab import *

im = array(Image.open("C-uniform01.ppm"))
m,n = im.shape[:2]

#调整图像的尺寸大小为（wid,wid）
wid = 50
rim = imresize(im,(wid,wid),interp='bilinear')
rim = array(rim,'f')

#创建归一化割矩阵
A = ncut.ncut_graph_matrix(rim,sigma_d=1,sigma_g=1e-2)

#聚类
code,V = ncut.cluster(A,k=3,ndim=3)

#变换到原来的图像大小
codeim = imresize(code.reshape(wid,wid),(m,n),interp='nearest')

#绘制分割结果
figure()
subplot(121)
imshow(im)
title('分割前图像')
subplot(122)
imshow(codeim)
title('分割后图像')
gray()
show()

实验结果：




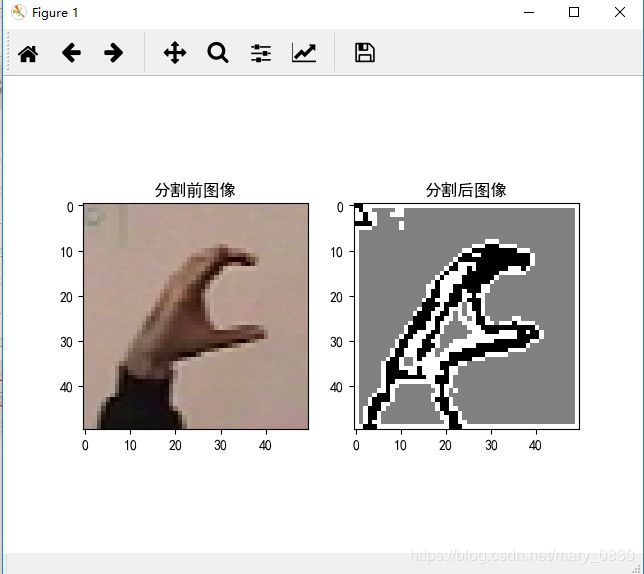
分析：
上面实验利用归一化分割算法分割图像，用到了静态手势“C”、“五”和小人图像，聚类数k均设置为3，都会显示三部分信息，把上面的图像都分成三部分。在上面的结果中，保持所有参数都一致，只修改了图像的内容，对图像进行阈值处理不会给出相同的结果，对RGB值或灰度值进行聚类也一样，其中原因是它们没有考虑像素的近邻。

（三）变分法

当优化的对象是函数时，该问题称为变分问题，解决这类问题的算法称为变分法。

概念：
变分法是17世纪末发展起来的一门数学分支，是处理函数的数学领域，和处理数的函数的普通微积分相对。它最终寻求的是极值函数：它们使得泛函取得极大或极小值。

变分法的关键定理是欧拉－拉格朗日方程。它对应于泛函的临界点。在寻找函数的极大和极小值时，在一个解附近的微小变化的分析给出一阶的一个近似。它分辨不出找到的是最大值还是最小值（或者两者都不是）。

变分法概念与寻常分析中的微分概念很为类似，但所联系的不是x的变化，而是函数y（x）的变化。 如果函数y（x）使U（y）达其极值，则U的变分δU变为0。（来自百度百科）

数学原理：
函数$y(x)$对于任意给定的输入变量$x$，给出输出值$y$；类似地，定义关于函数的函数$F[y]$，亦称泛函，给定函数$y$，输出值为$F$。熵$H[x]$也是泛函的一种，它定义在概率密度函数$p(x)$上，可等价记为$H[p]$。

泛函中变分法类似于函数中求极值点，即寻求某个最大化或最小化泛函$F[y]$的函数$y(x)$。利用变分法可证明两点之间的最短路径为直线以及最大熵分布为高斯分布。
对于多元函数$y(x)=y(x_1,...,x_D)$，其泰勒展开为：$$y(x+ϵ)=y(x)+{ϵ}^T\frac{\partial y}{\partial x}+O(\Vert ϵ{\Vert }^2).$$
对于某个泛函$F[y]$，考虑$y(x)$上的微小改变$ϵ\eta (x)$，其中$\eta (x)$为任意函数，对比上式，将$x$展开到无限维，从而：$$F[y(x)+ϵ\eta (x)]=F[y(x)]+\int \frac{\delta F}{\delta y(x)}ϵ\eta (x)dx+O({ϵ}^2),$$
其中$\delta F/\delta y(x)$为泛函梯度。

为了使$F[y]$取得极值，上式一阶条件为：$$\underset{ϵ\to 0}{\lim }\frac{\int \frac{\delta F}{\delta y(x)}ϵ\eta (x)dx}{ϵ}=\int \frac{\delta F}{\delta y(x)}\eta (x)dx=0$$
注意到η(x)选取的任意性，可得泛函梯度需要处处为零，即：$$\frac{\delta F}{\delta y(x)}\equiv 0.$$

Chan-Vese分割模型对于待分割图像区域假定一个分片常数图像模型。这里集中关注两个区域的情形，比如说是前景和背景，这个模型也可以扩展到多区域。如果用一组曲线$\Gamma$将图像分离成两个区域${\Omega }_1$和${\Omega }_2$，分割时通过最小化Chan-Vese模型能量函数给出的：$$E(\Gamma )=\lambda length(\Gamma )+{\int }_{{\Omega }_1}^{}(I-c_1{)}^{2}dx+{\int }_{{\Omega }_2}^{}(I-c_2{)}^{2}dx$$

模型如下所示，分片常数CV分割模型：

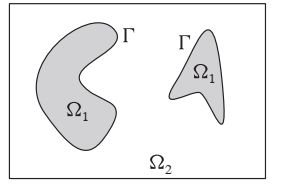
该能量函数用来度量与内部平均灰度常数$c_1$和外部平均灰度常数$c_2$的偏差。这里这两个积分是对各自区域的积分，分离曲线$\Gamma$的长度用以选择更平滑的方案。

由分片常数图像$U={\chi }_1{c}_1+{\chi }_2{c}_2$，可以将上面的式子重写为：$$E(\Gamma )=\lambda \frac{\left|c_1-c_2\right|}{2}\int \left|▽U\right|dx+{\Vert I-U\Vert }^2$$ ${\chi }_1$和${\chi }_2$是两区域${\Omega }_1$和${\Omega }_2$的特征（指示）函数。

注意： 区域内特征函数为1，区域外特征函数为0。

用变分法最小化CV模型转变成为设置阈值的ROF降噪问题，代码编写如下：

# -*- coding: utf-8 -*-
from numpy import *
from PIL import Image
from PCV.tools import graphcut
import ncut
from scipy.misc import imresize
from pylab import *
import rof

im = array(Image.open("boy_on_hill.jpg").convert('L'))
U,T = rof.denoise(im,im,tolerance=0.01)
t = 0.4  #阈值
title('原始图像')
imshow(im)
import scipy.misc
scipy.misc.imsave('result.pdf',U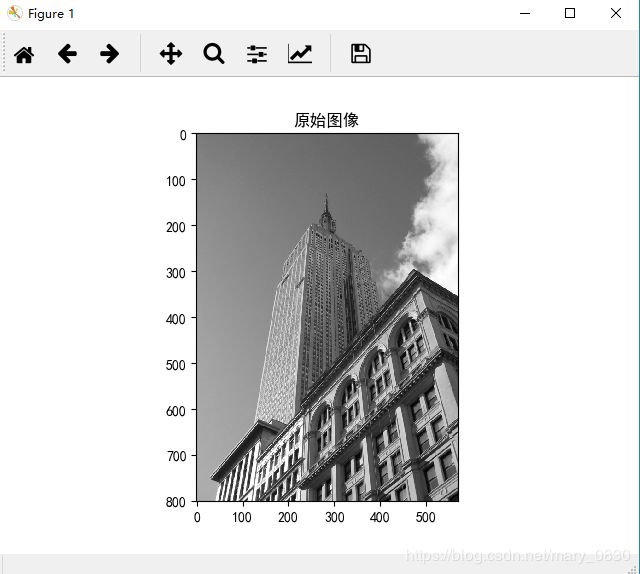

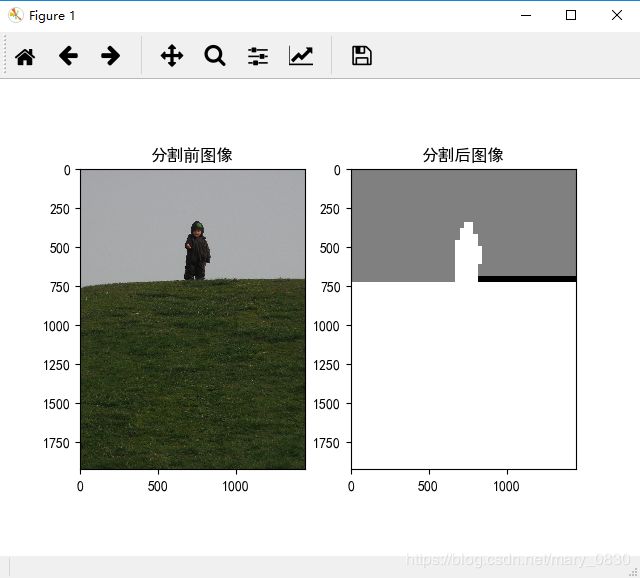
实验结果：

最终分割结果：




分析：
为确保得到足够的迭代次数，调低ROF迭代终止时的容忍阈值。利用ROF降噪最小化CV模型，得到如上面的分割结果。可以看出，图像灰度级越复杂，ROF迭代次数越多，降噪过程越久。

如果您在阅读之中发现文章错误之处或者出现疑问，欢迎在评论指出。