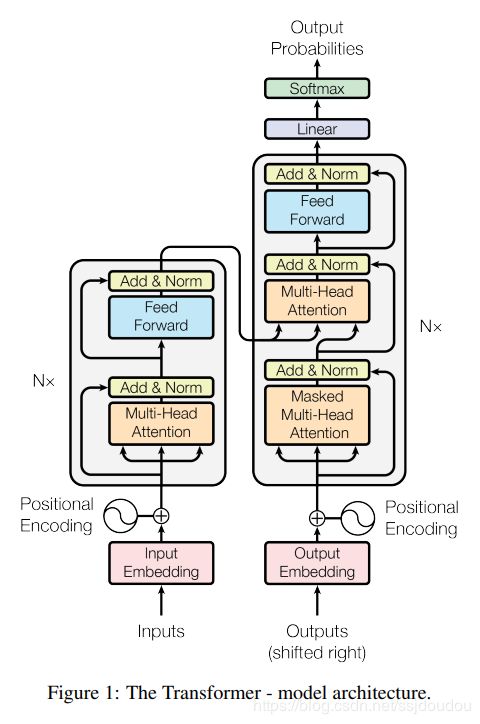
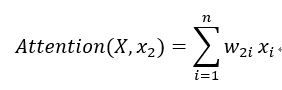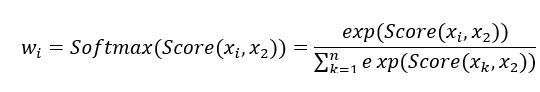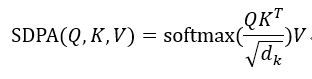Transformer全面详解

Time series on Transformer

Transformer Input

Transformer输入是一个序列数据，以"Tom chase Jerry" 翻译成中文"汤姆追逐杰瑞"为例：
Encoder 的 inputs就是"Tom chase Jerry" 分词后的词向量。可以是任意形式的词向量，如word2vec，GloVe，one-hot编码。

假设上图中每一个词向量都是一个512维的词向量。

Postions Encoding(PE)

transformer模型的attention机制并没有包含位置信息，即一句话中词语在不同的位置时在transformer中是没有区别的，就算打乱一句话中词语的位置，每个词还是能与其他词之间计算attention值，就相当于是一个功能强大的词袋模型，对结果没有任何影响。

I like this movie because it doesn't have an overhead history. Positive
I don't like this movie because it has an overhead history. Negative.

可以看出，don’t这个单词位置的不同，对整体句子的情感判别是完全相反的。

为了使模型能够利用序列的顺序，作者在transformer中引入了位置编码。在实现方式上，分为Facebook版本（《Convolutional Sequence to Sequence Learning》）和Google版本。作者形容前者为“learned and fixed”，即“Postional Embedding”，它只能表征有限长度内的位置，无法对任意位置进行建模。后者直接上了公式，改“Embedding”为“Encode”，想要多长就有多长。实验结果表明，两种形式的模型没有效果差别，但毕竟通过公式来计算更简单、参数量也更小：

论文中给出的Postions Encoding公式如下：
$$\{\begin{array}{ccc}PE(pos,2i)=sin(pos/10000^{2i/d_{model}})& & \\ PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}})& & \end{array}$$
其中，$d_{model}$ 是输入向量的维度；$pos$ 即 position，意为 token 在句中的位置，设句子长度为 $L$ ，则$pos=0,1,...,L-1$；$i$ 为向量的某一维度，例如 $d_{model}$ = 512时，$i=0,1,2,...,255$。

每个坐标位置的三角函数波长是不同的，论文中的范围从 $2\pi ->10000\ast 2\pi$。

这里**为什么用三角函数来表征编码位置？**我的理解是

传统的方法使用单调函数，使得任意后续的字符的位置编码都大于前面的字，来体现某个字在句子中的绝对位置，在本文中，放弃对绝对位置的追求，转而要求位置编码仅仅关注一定范围内的相对次序关系，那么使用一个sin/cos函数就是很好的选择，因为sin/cos函数的周期变化规律非常稳定，是有界的周期性函数，所以编码具有一定的不变性。至于为什么要使用10000呢，这个就类似于玄学了，原论文中完全没有提。至于$sinx/cosx$ 的交替使用只是为了使编码更「丰富」，在哪些维度上使用 $sin$，哪些使用 $cos$ ，不是很重要，都是模型可以调整适应的。

根据三角函数：
$$\{\begin{array}{ccc}sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta & & \\ cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta & & \end{array}$$

可得：
$$\{\begin{array}{ccc}PE(pos+k,2i)=PE(pos,2i)\times PE(k,2i+1)+PE(pos,2i+1)\times PE(k,2i)& & \\ PE(pos+k,2i+1)=PE(pos,2i+1)\times PE(k,2i+1)+PE(pos,2i)\times PE(k,2i)& & \end{array}$$

当求解$PE(pos+k,2i)$的向量时，可表示为对$PE(pos,2i)$上的线性表示，因为$PE(k,2i+1)$当每次k=1时就是一个固定的值，这样逐步向后推。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KYvNO7i2-1594572521167)(/Users/Arithmetic/Library/Application Support/typora-user-images/image-20200712204515106.png)]

为什么是将positional encoding与词向量相加，而不是拼接呢？
拼接相加都可以，只是本身词向量的维度512维就已经蛮大了，再拼接一个512维的位置向量，变成1024维，这样训练起来会相对慢一些，影响效率。两者的效果是差不多地，既然效果差不多当然是选择学习习难度较小的相加了。

为什么是这个公式？

很有可能是作者根据经验自己造的，而且公式也不是唯一地，后续Google在bert中的positional encoding也没有再使用这种方法而是通过训练PE。

为什么要用10000这个数？

我的理解是取一个较大的数，文本长度超过$10000\pi$就会进入第二个相同的周期，这个编码就会和第一个周期的编码有一点差异，但不会太大，如果让这个周期太大的话，也不行，大部分的编码都会集中在很小的区域里，相邻位置编码的差异变小。

Transformer Model

Self-Attention

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vaT2FieO-1594572521170)(/Users/Arithmetic/Library/Application Support/typora-user-images/image-20200703175043815.png)]

$X$ 表示输入序列集合 {$x_1,x_2,...x_n$}，$w_{2i}$ 表示在以为 $x_2$ 目标的计算过程中$x_i$ 的权重

$w_{2i}$ 决定于$x_i$ 和$x_2$ 的相关性 Score($x_i$ ,$x_2$ )，由于所有 X 都参与$x_2$ 对应的计算，所以使用 softmax 来保证所有权值之和等于 1。

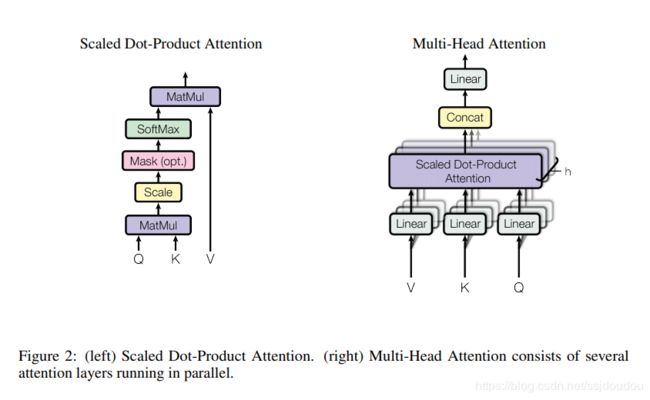
self-attention的输入是序列词向量，此处记为$x$。$x$经过一个线性变换得到$query(Q)$，$x$经过第二个线性变换得到$key(K)$， $x$经过第三个线性变换得到$value(V)$。

也就是：

• key(K) = linear_k(x)

• query(Q) = linear_q(x)

• value(V) = linear_v(x)

注意：这里的linear_k, linear_q, linear_v是相互独立、权重$(W^Q,W^K,W^V)$是不同的
$$Attention(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
$d_k=d_{model}/h=512/8$

Scaled Dot-Product Attention (SDPA)

常用的attention主要有“Add-相加”和“Mul-相乘”两种：
$$\begin{gathered} score(h_j,s_i)=<v,tanh(W_1{h}_j+W_2{s}_i)>[Add] \\ score(h_j,s_i)=<W_1{h}_j+W_2{s}_i)>[Mul] \end{gathered}$$
矩阵加法的计算更简单，但是外面套着$tanh$ 和$v$，相当于一个完整的隐层。在整体计算复杂度上两者接近，但考虑到矩阵乘法已经有了非常成熟的加速算法，Transformer采用了Mul形式。

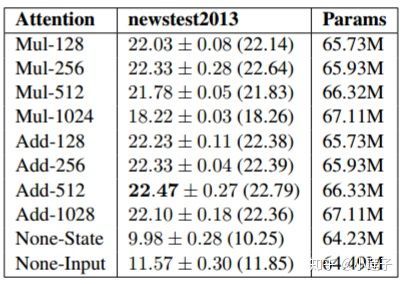
在模型效果上，《Massive Exploration of Neural Machine Translation Architectures》对不同Attention-Dimension（$d_k$ ）下的Add和Mul进行了对比，如下图：

可以看到，在$d_k$ 较小的时候，Add和Mul相差不大；随着$d_k$ 增大，Add明显超越了Mul。Transformer 设置$d_k=64$ ，虽然不在表格的范围内，但是可以推测Add仍略优于Mul。作者认为（怀疑），$d_k$ 的增大将点积结果推向了softmax函数的梯度平缓区，影响了训练的稳定性。

We suspect that for large values of dk, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients

缩放因子$\frac{1}{\sqrt{d_k}}$

• 缩放因子的作用是归一化
• 假设$Q,K$里的元素的均值为0，方差为1，那么 $A^T$ 中元素的均值为0，方差为$d$. 当$d$变得很大时， $A$中的元素的方差也会变得很大，如果$A$中的元素方差很大，那么$softmax(A)$ 的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。总结一下就是$softmax(A)$的分布会和d有关。因此$A$中每一个元素乘上$\frac{1}{\sqrt{d_k}}$ 后，方差又变为1。这使得$softmax(A)$ 的分布“陡峭”程度与$d$解耦，从而使得训练过程中梯度值保持稳定。

Muti-Head-Attention

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.

Multi-head Attention的本质是，在参数总量保持不变的情况下，将同样的query, key, value映射到原来的高维空间的不同子空间中进行attention的计算，在最后一步再合并不同子空间中的attention信息。这样降低了计算每个head的attention时每个向量的维度，在某种意义上防止了过拟合；由于Attention在不同子空间中有不同的分布，Multi-head Attention实际上是寻找了序列之间不同角度的关联关系，并在最后concat这一步骤中，将不同子空间中捕获到的关联关系再综合起来。

Add & Norm

Add

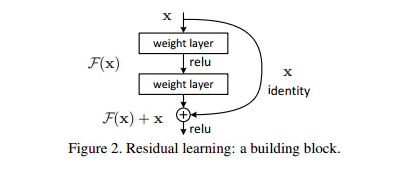
Add，就是在Z的基础上加了一个残差块X，加入残差块X的目的是为了防止在深度神经网络训练中发生退化问题，退化的意思就是深度神经网络通过增加网络的层数，Loss逐渐减小，然后趋于稳定达到饱和，然后再继续增加网络层数，Loss反而增大。

ResNet 残差神经网络

X是这一层残差块的输入，也称作$F(X)$为残差，$X$为输入值，$F(X)$是经过第一层线性变化并激活后的输出，该图表示在残差网络中，第二层进行线性变化之后激活之前，$F(X)$加入了这一层输入值$X$，然后再进行激活后输出。在第二层输出值激活前加入$X$，这条路径称作shortcut连接。

这个时候输出假设为$H(X)=F(X)+X$，我们要让$H(X)=X$，只需要让$F(X)=0$即可。神经网络通过训练变成0是比变成$X$容易很多的。并且ReLU能够将负数激活为0，过滤了负数的线性变化，也能够更快的使得F(x)=0。使用ResNet的网络很大程度上解决了学习恒等映射的问题，用学习残差F(x)=0更新该冗余层的参数来代替学习$h(x)=x$更新冗余层的参数。这样当网络自行决定了哪些层为冗余层后，通过学习残差$F(x)=0$来让该层网络恒等映射上一层的输入，使得有了这些冗余层的网络效果与没有这些冗余层的网络效果相同，这样很大程度上解决了网络的退化问题。
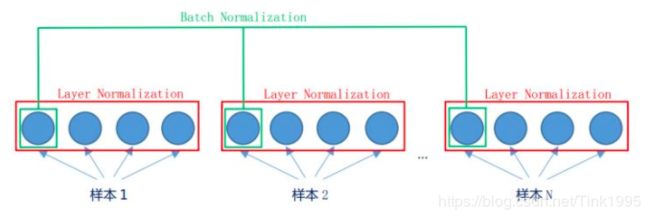
Normalize

对数据的归一化能够加快训练速度并且提高训练的稳定性

*Layer Normalization(LN)是在同一个样本中不同神经元之间进行归一化，而Batch Normalization(BN)*是在同一个batch中不同样本之间的同一位置的神经元之间进行归一化

Feed Forward Network

每一层经过attention之后，还会有一个FFN，这个FFN的作用就是空间变换。FFN包含了2层linear transformation层，中间的激活函数是ReLu。
$$FFN=max(0,x{W}_1+b_1)W_2+b_2$$

from typing import Optional

import torch
import torch.nn as nn
import torch.nn.functional as F


class PositionwiseFeedForward(nn.Module):
    """Position-wise Feed Forward Network block from Attention is All You Need.

    Apply two linear transformations to each input, separately but indetically. We
    implement them as 1D convolutions. Input and output have a shape (batch_size, d_model).

    Parameters
    ----------
    d_model:
        Dimension of input tensor.
    d_ff:
        Dimension of hidden layer, default is 2048.
    """

    def __init__(self,
                 d_model: int,
                 d_ff: Optional[int] = 2048):
        """Initialize the PFF block."""
        super().__init__()

        self._linear1 = nn.Linear(d_model, d_ff)
        self._linear2 = nn.Linear(d_ff, d_model)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """Propagate forward the input through the PFF block.

        Apply the first linear transformation, then a relu actvation,
        and the second linear transformation.

        Parameters
        ----------
        x:
            Input tensor with shape (batch_size, K, d_model).

        Returns
        -------
            Output tensor with shape (batch_size, K, d_model).
        """
        return self._linear2(F.relu(self._linear1(x)))

FFN的加入引入了非线性(ReLu激活函数)，变换了attention output的空间, 从而增加了模型的表现能力。

Mask-Multi-Head-Attention

Mask 的目的是防止 Decoder “seeing the future”，就像防止考生偷看考试答案一样。这里mask是一个下三角矩阵，对角线以及对角线左下都是1，其余都是0。下面是个10维度的下三角矩阵

1.padding mask
什么是 padding mask 呢？因为每个批次输入序列长度是不一样的也就是说，我们要对输入序列进行对齐。具体来说，就是给在较短的序列后面填充 0。但是如果输入的序列太长，则是截取左边的内容，把多余的直接舍弃。因为这些填充的位置，其实是没什么意义的，所以我们的attention机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。
具体的做法是，把这些位置的值加上一个非常大的负数(负无穷)，这样的话，经过 softmax，这些位置的概率就会接近0！

2.sequence mask
sequence mask 是为了使得 decoder 不能看见未来的信息。对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想一个办法，把 t 之后的信息给隐藏起来。这在训练的时候有效，因为训练的时候每次我们是将target数据完整输入进decoder中地，预测时不需要，预测的时候我们只能得到前一时刻预测出的输出。
那么具体怎么做呢？也很简单：产生一个上三角矩阵，上三角的值全为0。把这个矩阵作用在每一个序列上，就可以达到我们的目的。

上面可能忘记说了，在Encoder中的Multi-Head Attention也是需要进行mask地，只不过Encoder中只需要padding mask即可，而Decoder中需要padding mask和sequence mask。OK除了这点mask不一样以外，其他的部分均与Encoder一样啦~

Add＆Normalize也与Encoder中一样，接下来就到了Decoder中第二个Multi-Head Attention，这个Multi-Head Attention又与Encoder中有一点点不一样。

Code

class Transformer(nn.Module):
    """Transformer model from Attention is All You Need.

    A classic transformer model adapted for sequential data.
    Embedding has been replaced with a fully connected layer,
    the last layer softmax is now a sigmoid.

    Attributes
    ----------
    layers_encoding: :py:class:`list` of :class:`Encoder.Encoder`
        stack of Encoder layers.
    layers_decoding: :py:class:`list` of :class:`Decoder.Decoder`
        stack of Decoder layers.

    Parameters
    ----------
    d_input:
        Model input dimension.
    d_model:
        Dimension of the input vector.
    d_output:
        Model output dimension.
    q:
        Dimension of queries and keys.
    v:
        Dimension of values.
    h:
        Number of heads.
    N:
        Number of encoder and decoder layers to stack.
    attention_size:
        Number of backward elements to apply attention.
        Deactivated if ``None``. Default is ``None``.
    dropout:
        Dropout probability after each MHA or PFF block.
        Default is ``0.3``.
    chunk_mode:
        Swict between different MultiHeadAttention blocks.
        One of ``'chunk'``, ``'window'`` or ``None``. Default is ``'chunk'``.
    pe:
        Type of positional encoding to add.
        Must be one of ``'original'``, ``'regular'`` or ``None``. Default is ``None``.
    """

    def __init__(self,
                 d_input: int,
                 d_model: int,
                 d_output: int,
                 q: int,
                 v: int,
                 h: int,
                 N: int,
                 attention_size: int = None,
                 dropout: float = 0.3,
                 chunk_mode: bool = True,
                 pe: str = None):
        """Create transformer structure from Encoder and Decoder blocks."""
        super().__init__()

        self._d_model = d_model

        self.layers_encoding = nn.ModuleList([Encoder(d_model,
                                                      q,
                                                      v,
                                                      h,
                                                      attention_size=attention_size,
                                                      dropout=dropout,
                                                      chunk_mode=chunk_mode) for _ in range(N)])
        self.layers_decoding = nn.ModuleList([Decoder(d_model,
                                                      q,
                                                      v,
                                                      h,
                                                      attention_size=attention_size,
                                                      dropout=dropout,
                                                      chunk_mode=chunk_mode) for _ in range(N)])

        self._embedding = nn.Linear(d_input, d_model)
        self._linear = nn.Linear(d_model, d_output)
        self._linear2 = nn.Linear(18, 8)

        pe_functions = {
            'original': generate_original_PE,
            'regular': generate_regular_PE,
        }

        if pe in pe_functions.keys():
            self._generate_PE = pe_functions[pe]
        elif pe is None:
            self._generate_PE = None
        else:
            raise NameError(
                f'PE "{pe}" not understood. Must be one of {", ".join(pe_functions.keys())} or None.')

        self.name = 'transformer'

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """Propagate input through transformer

        Forward input through an embedding module,
        the encoder then decoder stacks, and an output module.

        Parameters
        ----------
        x:
            :class:`torch.Tensor` of shape (batch_size, K, d_input).

        Returns
        -------
            Output tensor with shape (batch_size, K, d_output).
        """
        K = x.shape[1]

        # Embeddin module
        encoding = self._embedding(x)

        # Add position encoding
        if self._generate_PE is not None:
            positional_encoding = self._generate_PE(K, self._d_model)
            positional_encoding = positional_encoding.to(encoding.device)
            encoding.add_(positional_encoding)

        # Encoding stack
        for layer in self.layers_encoding:
            encoding = layer(encoding)

        # Decoding stack
        decoding = encoding

        # Add position encoding
        if self._generate_PE is not None:
            positional_encoding = self._generate_PE(K, self._d_model)
            positional_encoding = positional_encoding.to(decoding.device)
            decoding.add_(positional_encoding)

        for layer in self.layers_decoding:
            decoding = layer(decoding, encoding)

        # Output module
        output = self._linear(decoding)
        output = self._linear2(torch.sigmoid(output).permute(0, 2, 1)).permute(0, 2, 1)

        return output

Encoder Model

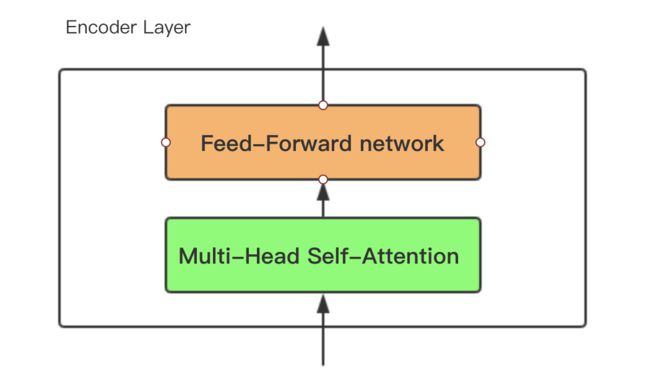
Encoder部分是由个层相同小Encoder Layer串联而成，小Encoder Layer可以简化为两个部分：

（1）Multi-Head Self Attention (2) Feed-Forward network。示意图如下:

Decoder Model

Decoder 也是N=6层堆叠的结构。被分为3个 SubLayer，Encoder与Decoder有三大主要的不同

（1）SubLayer-1 使用的是 “Masked” Multi-Headed Attention 机制，防止为了模型看到要预测的数据，防止泄露。

（2）SubLayer-2 是一个 Encoder-Decoder Multi-head Attention。

（3）LinearLayer 和 SoftmaxLayer 作用于 SubLayer-3 的输出后面，来预测对应的 word 的 probabilities

Model Features

Transformer是一种基于注意力的神经网络，用于解决NLP任务。它们的主要特点是：

优点：

• 特征向量维数的线性复杂度；
• 序列计算的并行化，与顺序计算相反；
• 长期记忆，可以直接观察任何输入的时序步骤。

缺点

在原文中没有提到缺点，是后来在Universal Transformers中指出的，主要是两点：

• 实践上：有些RNN轻易可以解决的问题transformer没做到，比如复制string，或者推理时碰到的sequence长度比训练时更长（因为碰到了没见过的position embedding）。

• 理论上：transformers不是computationally universal(图灵完备)，这种非RNN式的模型是非图灵完备的的，无法单独完成NLP中推理、决策等计算问题（包括使用transformer的bert模型等等）。

Model Structure

Transformer(
  (layers_encoding): ModuleList(
    (0): Encoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (1): Encoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (2): Encoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (3): Encoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
  )
  (layers_decoding): ModuleList(
    (0): Decoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_encoderDecoderAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm3): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (1): Decoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_encoderDecoderAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm3): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (2): Decoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_encoderDecoderAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm3): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
    (3): Decoder(
      (_selfAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_encoderDecoderAttention): MultiHeadAttention(
        (_W_q): Linear(in_features=64, out_features=64, bias=True)
        (_W_k): Linear(in_features=64, out_features=64, bias=True)
        (_W_v): Linear(in_features=64, out_features=64, bias=True)
        (_W_o): Linear(in_features=64, out_features=64, bias=True)
      )
      (_feedForward): PositionwiseFeedForward(
        (_linear1): Linear(in_features=64, out_features=2048, bias=True)
        (_linear2): Linear(in_features=2048, out_features=64, bias=True)
      )
      (_layerNorm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_layerNorm3): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
      (_dopout): Dropout(p=0.2, inplace=False)
    )
  )
  (_embedding): Linear(in_features=691, out_features=64, bias=True)
  (_linear): Linear(in_features=64, out_features=672, bias=True)
  (_linear2): Linear(in_features=18, out_features=8, bias=True)
)

Output

首先经过一次线性变换，然后Softmax得到输出的概率分布，然后通过词典，输出概率最大的对应的单词作为我们的预测输出。