线性规划
1.1 秘籍内容
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划,而线性规划(LinearProgramming 简记LP)则是数学规划的一个重要分支。此次练武旅程中,我们找来了两位大师带我们飞,一位是苏联数学家L.V.Kantorovich,另外是美国数学家G.B.Dantzig。
L.V.Kantorovich:练武之前,我们需了解此招数用途。线性规划是为了优化问题,什么是优化问题,通俗来说就是指用“最好”的方式,使用或分配有限的资源,包括我们所熟知的劳动力、原材料、机器、资金等,使得费用最小或是利润最大了,这也是我从经济学中感受出来数学的真谛。
G.B.Dantzig:康托洛维奇说的不错,那么我们知道了目的,就需要寻找方法去解决,这里就由我给大家讲解了。首先为了解决优化问题,我们的引出一些招式的概念来实现一般性:
1)问题的决策变量,一般用n维向量x=( x 1 x_1 x1, x 2 x_2 x2,…, x n x_n xn)T表示,也就是问题中待定的未知变量,我们用代数符号表示它们。
2)目标函数f(x),关于决策变量的线性函数。
3)可行域,决策变量x允许的取值范围。
4)约束条件,常用一系列关于决策变量的不等式组(或是等式或是两者交叉) g i g_i gi(x) ≤ \leq ≤ 0,(i=1,2,…,m)。
我们在构思的过程中,已经将数学引入进来而且具有一定的普遍性,可以说这是一个优化问题的数学模型,而它可表述为如下形式:
min z=f(x)
s.t. g i g_i gi(x) ≤ \leq ≤ 0,(i=1,2,…,m)
这类形式的模型叫线性规划模型,属于约束优化。
回顾上面的内容,我们会有关于建立线性规划模型的灵感,这些概念设出来肯定是有它们的用途,所以咱们得从这些一般概念出发寻找出线性规划模型的基本步骤。要练此功,需要学会三大招。
线性规划招式修炼三大法:
第一步,找出待定的未知变量(决策变量),并用代数符号表示它们
第二步,找出问题中所有的限制或约束,写出未知变量的线性方程或线性不等式
第三步,找到模型的目标或判据,携程决策变量的线性函数,以便求出其最大值或是最小值
L.V.Kantorovich:我们来用一下这“三步走”大法,看看是不是那么有效果。
广告现在天天见,甚至一些广告的特效堪比好莱坞大片。可在广告手段的选择中,一家广告公司想在电视、广播、杂志上做广告,其目的也是尽可能多地招徕顾客。下面是市场调查结果:

这家广告公司希望广告费用不超过800(千元),还有要求:(1)至上要有200万女性收看广告(2)电视广告费不超过500(千元);(3)电视广告白天至上播出至少三次,最佳时间至少播出2次;(4)通过广播、杂志做的广告要重复5到10次
第一步,确定决策变量,题目中要求的未知变量不就是白天电视、最佳时间电视、广播、杂志的广告次数吗?所以我们令 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3, x 4 x_4 x4 分别表示白天电视、最佳时间电视、广播、杂志的广告次数。
第二步,找出来所有约束条件。广告经费的约束;受广告影响的女顾客数的约束;电视广告的约束;由于广播和杂志广告次数都在5到10之间,这也是一个约束条件。我们来具体化:
广告经费的约束条件:40 x 1 x_1 x1+75 x 2 x_2 x2+30 x 3 x_3 x3+15 x 4 x_4 x4≤800
受广告影响的女顾客数的约束条件:300 x 1 x_1 x1+400 x 2 x_2 x2+200 x 3 x_3 x3+100 x 4 x_4 x4 ≥ \geq ≥ 2000
电视广告的约束条件:40 x 1 x_1 x1+75 x 2 x_2 x2≤500, x 1 x_1 x1 ≥ \geq ≥ 3, x 2 x_2 x2 ≥ \geq ≥ 2
最后一个约束条件:5 ≤ \leq ≤ x 3 x_3 x3 ≤ \leq ≤ 10,5 ≤ \leq ≤ x 4 x_4 x4 ≤ \leq ≤ 10(我们也直接写成5 ≤ \leq ≤ x 3 x_3 x3 , x 4 x_4 x4 ≤ \leq ≤ 10)。
第三步,我们要找目标,这道题目中,我们当然希望看广告的人多了,所以受每次广告影响的顾客数越多越好。则maxZ=400 x 1 x_1 x1+900 x 2 x_2 x2+500 x 3 x_3 x3+200 x 4 x_4 x4 为目标函数。
故完整规划如下:
maxZ=400 x 1 x_1 x1+900 x 2 x_2 x2+500 x 3 x_3 x3+200 x 4 x_4 x4
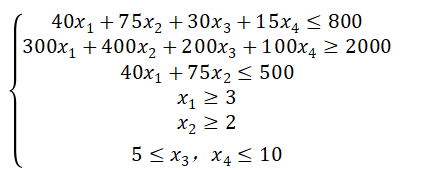
有时候还得考虑实际情况,比如该题中次数为非负数即 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3, x 4 x_4 x4 ≥ \geq ≥ 0,这也是隐藏的约束条件。
1.2 武器栏
G.B.Dantzig:模型建立了,该是我们解决的时候了,在理论上可以运用我发明的单纯形法来求解。朋友们,我们已经在21世纪,要充分利用身边的数学工具,所以我想先给大家介绍两种实际建模中常用的方法:MATLAB软件包解法和LINGO软件包解法,这也是我们线性规划派的俩个常用武器
1.2 .1 武器一 :MATLAB解线性规划
x=linprog(c,A,b)
用于求解模型:min z=cX
s.t A X ≤ b
2.
x=linprog(c,A,b,Aeq,beq)
用于求解模型:min z=c X
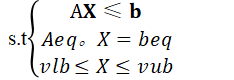
若没有不等式约束:AX≤b,则令A=[ ],b=[ ]
3.
x=linprog(c,A,b,Aeq,beq,vlb,vub)
用于求解模型:min z=c X
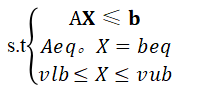
若没有等式约束:Aeq。X=beq,则令Aeq=[ ],beq=[ ]
4.
x=linprog(c,A,b,Aeq,beq,vlb,vub,),也用于模型3的求解,其中 X 0 X_0 X0 是初始点
5.
[x,fval]=linprog()
返回最优解x及x处的目标函数值fval
武器注解:
x = linprog( c , A , b , Aeq , beq , vlb , vub , X 0 X_0 X0 )是求解线性规划问题的命令。
c是目标函数的系数向量,A是不等式约束AX<=b的系数矩阵,b是不等式约束AX<=b的常数项。
Aeq是等式约束AeqX=beq的系数矩阵,beq是等式约束AeqX=beq的常数项,vlb是X的下限,vub是X的上限,X是向量[ x 1 x_1 x1, x 2 x_2 x2,…, x n x_n xn]即决策变量。
指定迭代的初始值 X 0 X_0 X0;
如果模型中不包含不等式约束条件,可用[]代替A和b表示缺省;如果没有等式约束条件,可用[]代替Aeq和beq表示缺省;如果某个xi无下界或上界,可以设定vlb(i)=-inf或vub(i)=inf;
用[x , fval]代替上述各命令行中左边的x,则可得到在最优解x处的函数值fval
牛刀小试
某厂每日8小时的产量不低于1800件。为了进行质量控制,计划聘请两种不同水平的检验员,且每种检验员的日产量不高于1800件。一级检验员的标准为:速度25件/小时,正确率98%,计时工资4元/小时;二级检验员的标准为:速度15件/小时,正确率95%,计时工资3元/小时。检验员每错检验一次,工厂要损失2元。为使总检验费用最省,该工厂应聘一级、二级检验员各几名?
设需要一级检验员和二级检验员的人数分别为 x 1 x_1 x1, x 2 x_2 x2,则应付检验员的工资为
8x4x x 1 x_1 x1+8x3x x 2 x_2 x2=32 x 1 x_1 x1+24 x 2 x_2 x2
因检验员错检而造成的损失为
(8x25x2%x x 1 x_1 x1+8x15x95%x x 2 x_2 x2)x2=8 x 1 x_1 x1+12 x 2 x_2 x2
故目标函数为
Min z=32 x 1 x_1 x1+24 x 2 x_2 x2+8 x 1 x_1 x1+12 x 2 x_2 x2=40 x 1 x_1 x1+36 x 2 x_2 x2
约束条件:
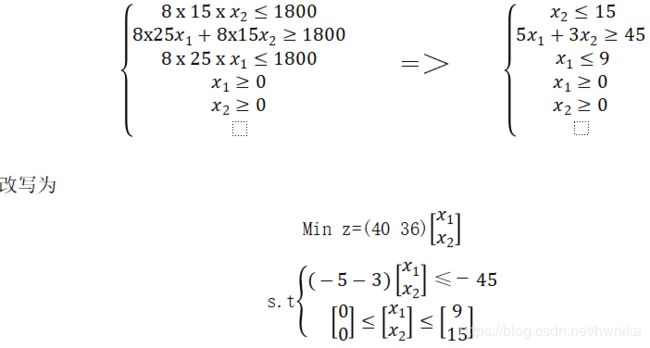
运用武器MATLAB后的奥义如下图:

即只需9个一级检验员
1.2 .2 武器二 :Lingo解线性规划
Lingo的攻击范围更广,和lingo武器可以切合的招式更多:比如非线性规划,那些不是纯整数规划的线性规划
在线性规划中的应用max Z =5 x 1 x_1 x1+3 x 2 x_2 x2+6 x 3 x_3 x3,

武器注解:
REDUCED COST 表示决策变量Xi的值由0变为非0而要求目标系数Ci进行改变的数量。类似于管理运筹学中文版软件中的“相差值”。
一般reduced cost不为0时,xi的最优解为0。
假如A产品的价格为50元,B产品的价格为30元。则求max z =50 x 1 x_1 x1+30 x 2 x_2 x2
而用lingo求解结果为
variable value reduced cost
x1 30 0
x2 0 20
如上,reduced cost 为20的意思就是说,想要生产B产品,就要B的价格由当前的30增加到50,即30加上reduced cost 20元的时候才可以进行生产。