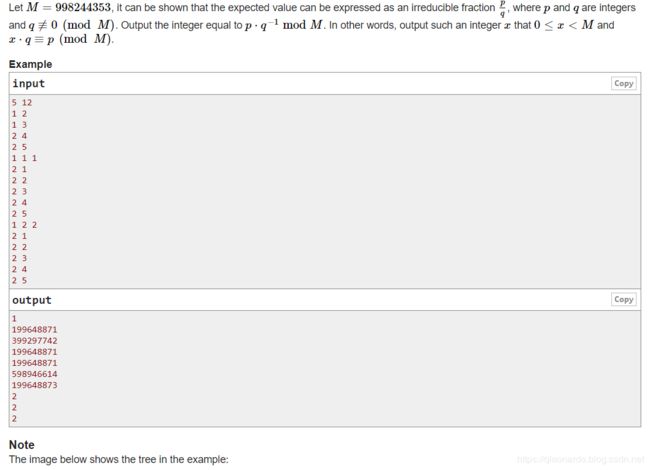
CodeForces - 1254D Tree Queries（树链剖分 + 树状数组 + 组合计数）

题意

两种操作。

第一种操作$(v,d)$，首先随机选择一个点$r$，然后把所有满足路径$<u,r>$经过$v$的$u$点都加上权值d。

第二种操作询问点$x$期望权值。

做法

显然要考虑每个询问对于单个点的贡献。

以样例为例，对于每一个操作$(v,d)$，考虑对节点2产生的贡献，可以分为两种情况。

当$v$在节点2所在的子树中时，显然$r$只要取$v$的子树中的点就可以对节点2产生贡献，因此产生的贡献就是$\frac{size[v]}{n}\ast d$。

当$v$不在节点2所在的子树中时，$r$只要不取在$v$的节点2所在的那个儿子的子树中就可以产生贡献，我们不妨设这个儿子为$y$，那么产生的贡献就是$\frac{n-size[y]}{n}\ast d$。

这样，我们发现，对于一个操作$(v,d)$，所有$v$子树以外的点，他们的贡献都是$\frac{size[v]}{n}\ast d$；子树内的点，贡献是$\frac{n-size[y]}{n}\ast d$，其中$y$随着所在节点的不同而变化。对于子树外的节点，我们直接用$dfs$序区间操作即可。对于子树内的节点，$v$的每一个儿子修改的数值不一样，直接枚举儿子显然会超时，这里我们有两种解决方式。一是考虑到修改数值只与子树大小有关，于是可以把儿子按照子树大小排序，把子树大小相同的合并，这样最坏情况下时间复杂度是$O(N\sqrt{n}logN)$，可以压线过。

另一种方法考虑树链剖分，在每次操作的时候，考虑把$d$放到节点$v$上。这样，我们要实现的操作无非是看祖先中，有多少个祖先的父亲上放过$d$，然后对应把这些操作的变化统计上去。所以，对于一个操作$(v,d)$，首先直接区间修改它的重儿子所在的子树，然后把$d$记录在$v$上。每次在查询的时候，按照重链去跳，直接统计链头上的操作的贡献即可。如此，时间复杂度是$O(NlogN)$。

代码

//只给出树链剖分代码
#include
#define PI 3.1415926535
#define fi first
#define se second
#define LL long long
#define pb push_back
#define lb lower_bound
#define INF 0x3f3f3f3f
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)

using namespace std;

const int N=150010;
const int mod = 998244353;
const int inv2 = (mod + 1) / 2;

std::vector<int> g[N];
int idx,id[N],c[N],top[N],son[N],sz[N],fa[N],w[N];

inline void update(int x,int y)
{
	for(int i=x;i<N;i+=i&-i)
		c[i]=(c[i]+y)%mod;
}

inline int getsum(int x)
{
	int res=0;
	for(int i=x;i;i-=i&-i)
		res=(res+c[i])%mod;
	return res;
}

inline void upd(int l,int r,int x)
{
    update(l,x);
    update(r+1,mod-x);
}

void dfs1(int u,int f)
{
    son[u]=0; sz[u]=1;
	for(auto y:g[u])
		if (y!=f)
		{
			fa[y]=u;dfs1(y,u);sz[u]+=sz[y];
			if (sz[y]>sz[son[u]]) son[u]=y;
		}
}

void dfs2(int u,int f)
{
	top[u]=f; id[u]=++idx;
	if (son[u]) dfs2(son[u],f);
	for(auto y:g[u])
		if (y!=son[u]&&y!=fa[u]) dfs2(y,y);
}

LL qpow(LL x,LL n)
{
	LL res=1;
	while(n)
	{
		if (n&1) res=res*x%mod;
		x=x*x%mod; n>>=1;
	}
	return res;
}

int main()
{
	int n,q;
	scc(n,q);
	int inv=qpow(n,mod-2);
	for(int i=1;i<n;i++)
	{
		int x,y; scc(x,y);
		g[x].pb(y); g[y].pb(x);
	}
	dfs1(1,0); dfs2(1,1);
	while(q--)
	{
		int op; sc(op);
		if (op==1)
		{
			int v,d,tmp; scc(v,d);
			tmp=(LL)sz[v]*d%mod;
			w[v]=(w[v]+d)%mod; update(1,tmp);
			upd(id[v],id[v]+sz[v]-1,mod-tmp);
			if (!son[v]) continue;
			upd(id[son[v]],id[son[v]]+sz[son[v]]-1,(LL)(n-sz[son[v]])*d%mod);
		} else
		{
			int x,res; sc(x);
			res=(getsum(id[x])+(LL)w[x]*n%mod)%mod;
			for(x=top[x];fa[x];x=top[fa[x]]) res=(res+(LL)(n-sz[x])*w[fa[x]]%mod)%mod;
			printf("%d\n",(LL)res*inv%mod);
		}
	}
}