椭圆曲线加密算法,即:Elliptic Curve Cryptography,简称ECC,是基于椭圆曲线数学理论实现的一种非对称加密算法。相比RSA,ECC优势是可以使用更短的密钥,来实现与RSA相当或更高的安全。据研究,160位ECC加密安全性相当于1024位RSA加密,210位ECC加密安全性相当于2048位RSA加密。
椭圆曲线在密码学中的使用,是1985年由Neal Koblitz和Victor Miller分别独立提出的。
椭圆曲线
一般情况下,椭圆曲线可用下列方程式来表示,其中a,b,c,d为系数。
E:y2=ax3+ bx2+cx+d
例如,当a=1,b=0,c=-2,d=4时,所得到的椭圆曲线为:
E:y2=x3-2x+4
该椭圆曲线E的图像如图X-1所示,可以看出根本就不是椭圆形。
定义椭圆曲线的运算规则
加法
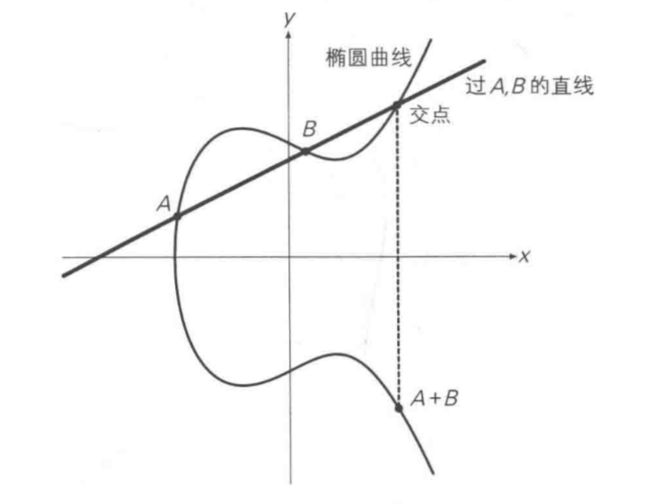
过曲线上的两点A、B画一条直线,找到直线与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A+B,即为加法。如下图所示:A + B = C
二倍运算
上述方法无法解释A + A,即两点重合的情况。因此在这种情况下,将椭圆曲线在A点的切线,与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A + A,即2A,即为二倍运算。
正负取反
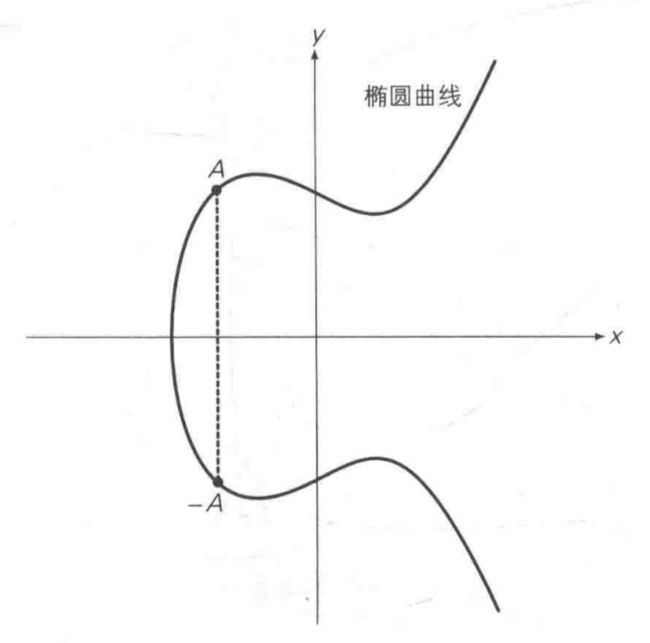
将A关于x轴对称位置的点定义为-A,即椭圆曲线的正负取反运算。如下图所示:
无穷远点
如果将A与-A相加,过A与-A的直线平行于y轴,可以认为直线与椭圆曲线相交于无穷远点。
综上,定义了A+B、2A运算,因此给定椭圆曲线的某一点G,可以求出2G、3G(即G + 2G)、4G......。即:当给定G点时,已知x,求xG点并不困难。反之,已知xG点,求x则非常困难。此即为椭圆曲线加密算法背后的数学原理。
有限域上的椭圆曲线运算
椭圆曲线要形成一条光滑的曲线,要求x,y取值均为实数,即实数域上的椭圆曲线。但椭圆曲线加密算法,并非使用实数域,而是使用有限域。按数论定义,有限域GF(p)指给定某个质数p,由0、1、2......p-1共p个元素组成的整数集合中定义的加减乘除运算。
假设椭圆曲线为y² = x³ + x + 1,其在有限域GF(23)上时,写作: y² ≡ x³ + x + 1 (mod 23)
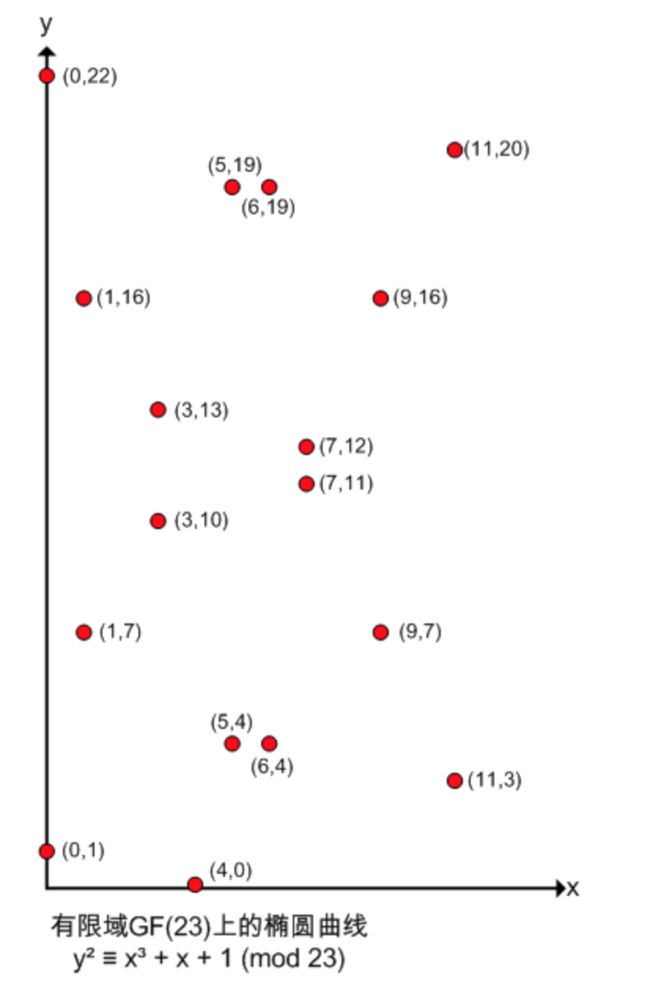
此时,椭圆曲线不再是一条光滑曲线,而是一些不连续的点,如下图所示。以点(1,7)为例,7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此还有如下点:
(0,1) (0,22) (1,7) (1,16) (3,10) (3,13) (4,0) (5,4) (5,19) (6,4) (6,19) (7,11) (7,12) (9,7) (9,16) (11,3) (11,20) 等等。
另外,如果P(x,y)为椭圆曲线上的点,则-P即(x,-y)也为椭圆曲线上的点。如点P(0,1),-P=(0,-1)=(0,22)也为椭圆曲线上的点。
计算xG
相关公式如下: 有限域GF(p)上的椭圆曲线y² = x³ + ax + b,若P(Xp, Yp), Q(Xq, Yq),且P≠-Q,则R(Xr,Yr) = P+Q 由如下规则确定:
Xr = (λ² - Xp - Xq) mod p Yr = (λ(Xp - Xr) - Yp) mod p 其中λ = (Yq - Yp)/(Xq - Xp) mod p(若P≠Q), λ = (3Xp² + a)/2Yp mod p(若P=Q)
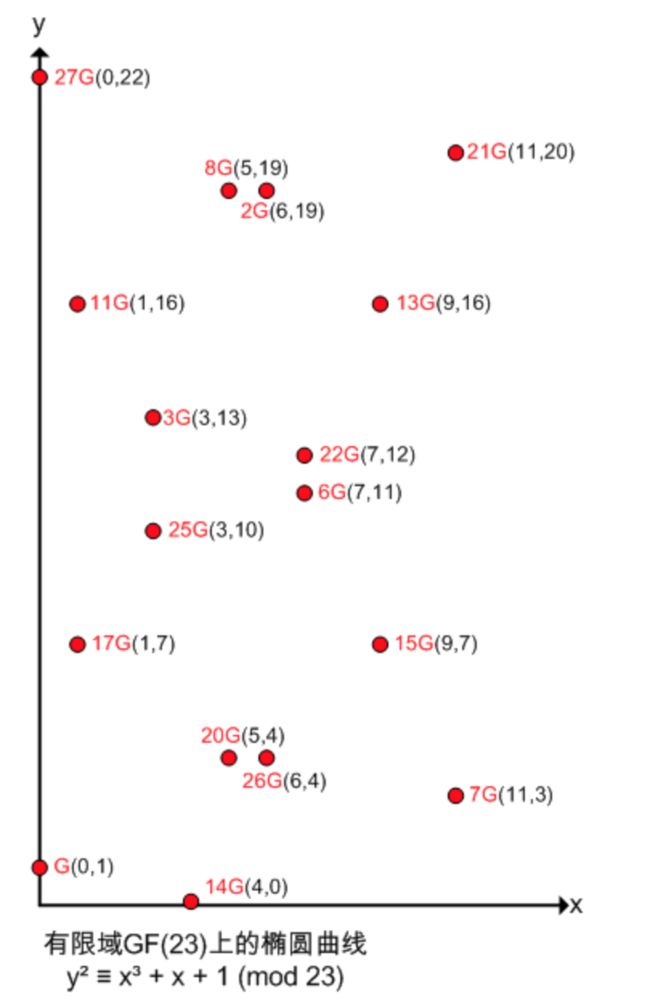
因此,有限域GF(23)上的椭圆曲线y² ≡ x³ + x + 1 (mod 23),假设以(0,1)为G点,计算2G、3G、4G...xG等等,方法如下:
计算2G: λ = (3x0² + 1)/2x1 mod 23 = (1/2) mod 23 = 12 Xr = (12² - 0 - 0) mod 23 = 6 Yr = (12(0 - 6) - 1) mod 23 = 19 即2G为点(6,19)
计算3G: 3G = G + 2G,即(0,1) + (6,19) λ = (19 - 1)/(6 - 0) mod 23 = 3 Xr = (3² - 0 - 6) mod 23 = 3 Yr = (3(0 - 3) - 1) mod 23 = 13 即3G为点(3, 13)
同理计算4G、5G...xG,分布如下图:椭圆曲线加解密算法原理
建立基于椭圆曲线的加密机制,需要找到类似RSA质因子分解或其他求离散对数这样的难题。而椭圆曲线上的已知G和xG求x,是非常困难的,此即为椭圆曲线上的的离散对数问题。此处x即为私钥,xG即为公钥。
椭圆曲线加密算法原理如下:
设私钥、公钥分别为k、K,即K = kG,其中G为G点。
公钥加密: 选择随机数r,将消息M生成密文C,该密文是一个点对,即: C = {rG, M+rK},其中K为公钥
私钥解密: M + rK - k(rG) = M + r(kG) - k(rG) = M 其中k、K分别为私钥、公钥。
椭圆曲线签名算法原理
椭圆曲线签名算法,即ECDSA。 设私钥、公钥分别为k、K,即K = kG,其中G为G点。
私钥签名: 1、选择随机数r,计算点rG(x, y)。 2、根据随机数r、消息M的哈希h、私钥k,计算s = (h + kx)/r。 3、将消息M、和签名{rG, s}发给接收方。
公钥验证签名: 1、接收方收到消息M、以及签名{rG=(x,y), s}。 2、根据消息求哈希h。 3、使用发送方公钥K计算:hG/s + xK/s,并与rG比较,如相等即验签成功。
原理如下: hG/s + xK/s = hG/s + x(kG)/s = (h+xk)G/s = r(h+xk)G / (h+kx) = rG
签名过程
假设要签名的消息是一个字符串:“Hello World!”。DSA签名的第一个步骤是对待签名的消息生成一个消息摘要。不同的签名算法使用不同的消息摘要算法。而ECDSA256使用SHA256生成256比特的摘要。
摘要生成结束后,应用签名算法对摘要进行签名:
产生一个随机数k
利用随机数k,计算出两个大数r和s。将r和s拼在一起就构成了对消息摘要的签名。
这里需要注意的是,因为随机数k的存在,对于同一条消息,使用同一个算法,产生的签名是不一样的。从函数的角度来理解,签名函数对同样的输入会产生不同的输出。因为函数内部会将随机值混入签名的过程。
验证过程
关于验证过程,这里不讨论它的算法细节。从宏观上看,消息的接收方从签名中分离出r和s,然后利用公开的密钥信息和s计算出r。如果计算出的r和接收到的r值相同,则表示验证成功。否则,表示验证失败。
package main
import (
"fmt"
"crypto/ecdsa"
"crypto/elliptic"
"crypto/rand"
"crypto/sha256"
"math/big"
)
func main() {
//明文
message := []byte("Hello world")
key, err := NewSigningKey()
if err != nil {
return
}
signature, err := Sign(message, key)
fmt.Printf("签名后:%x\n", signature)
if err != nil {
return
}
if !Verify(message, signature, &key.PublicKey) {
fmt.Println("验证失败!")
return
}else{
fmt.Println("验证成功!")
}
}
func NewSigningKey() (*ecdsa.PrivateKey, error) {
key, err := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
return key, err
}
// Sign signs arbitrary data using ECDSA.
func Sign(data []byte, privkey *ecdsa.PrivateKey) ([]byte, error) {
// hash message
digest := sha256.Sum256(data)
// sign the hash
r, s, err := ecdsa.Sign(rand.Reader, privkey, digest[:])
if err != nil {
return nil, err
}
// encode the signature {R, S}
// big.Int.Bytes() will need padding in the case of leading zero bytes
params := privkey.Curve.Params()
curveOrderByteSize := params.P.BitLen() / 8
rBytes, sBytes := r.Bytes(), s.Bytes()
signature := make([]byte, curveOrderByteSize*2)
copy(signature[curveOrderByteSize-len(rBytes):], rBytes)
copy(signature[curveOrderByteSize*2-len(sBytes):], sBytes)
return signature, nil
}
// Verify checks a raw ECDSA signature.
// Returns true if it's valid and false if not.
func Verify(data, signature []byte, pubkey *ecdsa.PublicKey) bool {
// hash message
digest := sha256.Sum256(data)
curveOrderByteSize := pubkey.Curve.Params().P.BitLen() / 8
r, s := new(big.Int), new(big.Int)
r.SetBytes(signature[:curveOrderByteSize])
s.SetBytes(signature[curveOrderByteSize:])
return ecdsa.Verify(pubkey, digest[:], r, s)
}