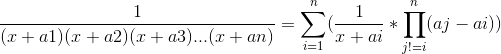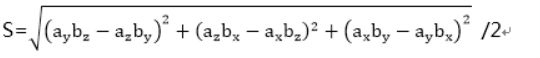2019牛客暑期多校训练营（第一场）A B F J

题目链接：https://ac.nowcoder.com/acm/contest/881#question

---

Problem A

题意：询问1~n最长区间使得1~n任意子区间询问都有数列的最小值在同一位置。

被队友教会了。

假设P为所求的答案，检查当前P是否合法，由于P具有当前不合法，P+1~n都不可能合法的性质，所以可以使用二分，若当前P合法，那么二分左指针右移，否则右指针左移。

O(n*logn)ST表维护两个数组各自的区间最小下标，这样每次都可以做到O（1）查询

然后判断当前P是否合法的方法是首先判断1~P两个数的最小值下标是否相同。

如果相同，假设这个下标为m，我们可以得知分别处于m两边的l，r的最小值下标一定是m，所以我们只需判断【1，m-1】，【m+1，P】是否合法即可，于是就递归着做就可以，一旦出现一个一个不合法就返回false，二分找下一个可行的P

#include
#include
#include

using namespace std;

#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;ir) return true;
    else if ( query(l,r) ){
        int minpos = qquery(l,r);
        return check(l,minpos-1) && check(minpos+1,r);
    }
    return false;
}

int main()
{
    int n;
    while (~scanf("%d",&n)){
        for1(i,1,n) rd(a[i]);
        for1(i,1,n) rd(b[i]);

        ST(sta,a,n);
        ST(stb,b,n);

        int l = 1,r = n;

        while (l<=r){
            int p = l+r>>1;
            bool flag = check(1,p);
            if (flag) l = p+1;
            else r = p-1;
        }

        printf("%d\n",r);
    }
    return 0;
}

---

Problem B

数理完蛋。

从这题得出的结论是：

①积分内的常数可以直接移到外面

②积分n项的积不能先各自积分再求积，累加的话是可以的。

③

④累乘变累加：

之后就是求逆元，累加就完事了

#include
#include
#include

using namespace std;

#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;i>= 1;
        a = a*a%mod;
    }
    return ans;
}

ll GETA(int idx)///求得当前下标对应的分母一坨值
{
    ll sum = 1;
    for1(i,1,n){
        if (i!=idx) sum = sum*(v[i]-v[idx])%mod;
    }
    sum = sum*a[idx]%mod*2%mod;
    return (sum+mod)%mod; ///上面涉及减法，最后记得加个这个
}

int main()
{
    while (~scanf("%d",&n)){
        for1(i,1,n) scanf("%lld",a+i),v[i] = a[i]*a[i]%mod;
        ll ans = 0;
        for1(i,1,n) ans = (ans+ GETNY(GETA(i)))%mod;

        printf("%lld\n",ans);

    }
    return 0;
}

---

Problem F

向量叉积求三角形：假设两条边的向量为（x1，y1），（x2，y2），

那么面积 = （×）/2 = abs（x1*y2-x2*y1）/2

顺便说一下三维的两条边叉乘可以求体积

V = 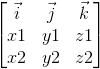  /2= (y1*z2-y2*z1, x2*z1-x1*z2, x1*y2-y1*x2) / 2 = ...

网上盗图：

然后期望到底是面积的几分之几直接爆交猜，emm

等于三角形面积的11/18，就当结论记住吧。

#include
#include
#include

using namespace std;

#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;i

---

Problem J

除法变乘法，涉及到大数的操作

把1e18的拆成1e9的大位，1e9的小位即可。

#include
#include
#include
#include

using namespace std;

#define ll long long
#define for1(i,a,b) for (int i=a;i<=b;i++)
#define for0(i,a,b) for (int i=a;i");
        else printf("%s\n",(x1");

    }
    return 0;
}

之后随缘补辽，有太多的东西不会了o(╥﹏╥)o