算法导论第25章 所有结点对的最短路径问题Floyd等
最短路径的结构:一条最短路径的所有子路径都是最短路径,
这篇中算法用到的都是邻接矩阵的存储方法,
0 if i == j
矩阵中w[i][j]: 有向边(i, j)的权重 if i != j 且(i, j) 属于E
INFINITE if i != j 且(i, j)不属于E
所有结点对最短路径问题的递归解:
设lij(m):是从结点i到结点j的至多包含m条变的任意路径中的最小权重,
当m = 0 时,结点i到结点j之间存在一条没有变的最短路径当且仅当i== j
if i== j, lij(m) = 0 else lij(m) = INFINITE
对于m >= 1, 需要计算的lij(m)是lij(m-1)的最小值,和从i到j最多有m条边组成的任意路径的最小权重,通过对j的所有前驱k检查来获得该值,
递归定义式是: lij(m) = min(lij(m-1), min(lik(m-1) + wkj) ) = min(lik(m-1) + wkj) ( 0 <= k <= n)
自底向上的计算最短路径的算法 :
核心算法是externShortestPaths():程序在给定W和L(m-1)的情况下计算出L(m), 代码将最近计算出的最短路径扩展了一条边。
算法用了三层循环,运行时间为Θ(n*n*n),该算法与矩阵相乘算法非常类似。
书中先介绍了一个Θ(n*n*n*n)时间内计算出最短路径的算法slowAllPathsShortestPaths,因为L(n-1)即为求出的最短路径矩阵,所以对externShortestPaths(),循环运行n-2次,一步一步扩展求出L(n-1),而L1 = W;
之后有介绍了一个改进算法运行时间的fastAllPathsShortestPaths算法,这个算法使用重复平方技术来计算矩阵序列,每次由两个L(m)得出L(2m),所以减小了需要求出的矩阵的个数,因为我们感兴趣的只是L(n-1),所以不用将每个矩阵都计算出来,而使用平方的方式,总共需要计算lg(n-1)个矩阵,而每个矩阵的计算时间是Θ(n*n*n),因此将算法运行时间减小到Θ(n*n*n*lgn)
之后就开始介绍到了Flod算法!!算法的运行时间是O(n*n*n), 考虑的是一条最短路径上的中间结点
使用的最短路径递归公式是与前面不同的,dij(k)为从结点i到结点j的所有中间结点全部取自集合{1, 2, ...., k}的一条最短路径的权重,
当k = 0 时,从结点i到结点j的一条不包括编号大于0的中间结点的路径将没有任何中间结点,dij(0) = wij
wij if k == 0
dij(k) =
min(dij(k-1), dik(k-1) + dkj(k-1)) if k >= 1
对于任何路径来说,所有的中间结点都属于集合{1, 2, ..., n},矩阵D(n)= (dij(n))给出的就是我们最后的答案,对于所有的i, j 属于V,dij(n)= δ(i,j)
Floyd算法又嵌套的三层for循环,所以运行时间为Θ(n*n*n)
关于最短路径的构建,可以在计算矩阵D(k)的同时计算前驱矩阵P,即也将计算一个矩阵序列P(0),P(1),...,P(n),P(n)定义pij(k)为从结点i到结点j的一条所有中间结点都取自集合{1,2,...,K}的最短路径上j的前驱结点。
pij(k)的递归公式是, 当k = 0时,从i到j没有中间结点,因此 NIL if i == j | wij = INFINITE
pij(0) = i if i != j && wij < INFINITE
如果k >= 1 pij(k-1) if dij(k-1) <= dik(k-1) + dkj(k-1) i到j的最短路径还是dij(k-1),所以j的前驱即为pij(k-1)
pij(k) =
pkj(k-1) if dij(k-1) > dik(k-1) + dkj(k-1) i到j的最短路径改为 dik(k-1) + dkj(k-1) ,有一个中间结点k,i到j的路径中的前驱即为k到j路径中j的前驱
代码中用到的图为:
以下为代码:
#ifndef MGRAPH_H
#define MGRAPH_H
#include
using namespace std;
//枚举类型,图的种类 DG:有向图;WDG:带权值的有向图;
//UDG: 无向图;WUDG: 带权值的无向图
enum GraphKind {DG, WDG, UDG, WUDG};
const int SIZE = 5; //定义二维数组的维度
typedef int (*pArray)[SIZE]; //定义二维数组返回指针
//vertexType顶点类型,VRType:顶点之间的关系类型,InfoType:弧的信息类型
template
class MGraph
{
public:
MGraph(int vexNum, GraphKind __kind) : vexnum(vexNum), arcnum(0), kind(__kind)
{
//分配顶点向量数组
vvec = new VertexType[vexnum];
//动态分配二维数组, 注意二维数组的动态分配
arcs = new int *[vexnum];
for (int i = 0; i < vexnum; i++)
{
//为每一行动态分配空间
arcs[i] = new int[vexnum];
}
}
//初始化邻接矩阵
void InitArcs()
{
for (int i = 0; i < vexnum; i++)
{
for (int j = 0; j < vexnum; j++)
{
if ((kind == WUDG || WDG) && i != j)
arcs[i][j] = INFINITE;
else
arcs[i][j] = 0;
}
}
}
void CreateWDG1()
{
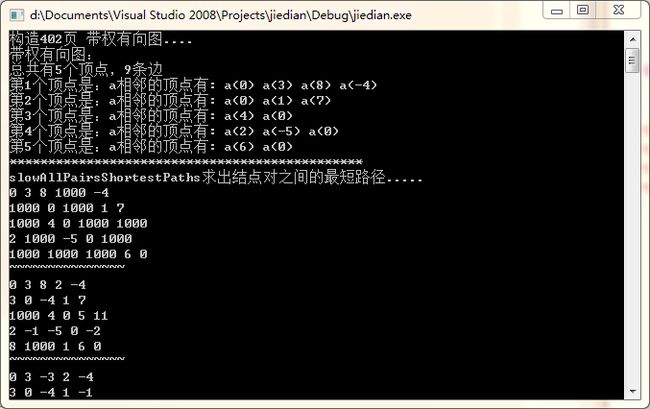
cout << "构造402页 带权有向图...." << endl;
//构造顶点数组
for (int i = 0; i < vexnum; i++)
{
vvec[i] = 'a' + 0;
}
InitArcs();
//构造边
insertArc(0, 1, 3);
insertArc(0, 2, 8);
insertArc(0, 4, -4);
insertArc(1, 3, 1);
insertArc(1, 4, 7);
insertArc(2, 1, 4);
insertArc(3, 2, -5);
insertArc(3, 0, 2);
insertArc(4, 3, 6);
cout << "带权有向图:" << endl;
}
//构造边
void insertArc(int vhead, int vtail, int weight)
{
arcs[vhead][vtail] = weight;
arcnum++;
}
void displayGraph()
{
cout << "总共有" << vexnum << "个顶点,"
<< arcnum << "条边" << endl;
for (int i = 0; i < vexnum; i++)
{
cout << "第" << i+1 << "个顶点是:" << vvec[i]
<< "相邻的顶点有: ";
for (int j = 0; j < vexnum; j++)
{
if (arcs[i][j] != INFINITE)
cout << vvec[j] << "(" << arcs[i][j] << ") ";
}
cout << endl;
}
cout << "**********************************************" << endl;
}
/*******************************************************************
带返回值的结点对最短路径算法,二维数组全部采用动态分配new的方式申请,所以在
delete []之前,二维数组一直存在,所以可以当返回值传出去。
*******************************************************************/
int** externShortestPaths(int **L, int **W)
{
//分配Lnext数组, 根据L和arcs来计算出Lnext, 在L的基础上再多加一条边
int **Lnext = new int*[SIZE];
for (int i = 0; i < SIZE; i++)
{
Lnext[i] = new int[SIZE];
}
for (int i = 0; i < vexnum; i++)
{
for (int j = 0; j < vexnum; j++)
{
Lnext[i][j] = INFINITE;
for (int k = 0; k < vexnum; k++)
{
//Lnext[i][j]的值为L[i][k]每次加上一条边的权重的最小值
// 0 < k < vexnum,相当于将所有的边都加到原来的最小值上过一遍。
if (L[i][k] + W[k][j] < Lnext[i][j])
Lnext[i][j] = L[i][k] + W[k][j];
}
}
}
return Lnext;
}
int** slowAllPairsShortestPaths()
{
cout << "slowAllPairsShortestPaths求出结点对之间的最短路径....." << endl;
int **p; //指向前一个二维数组
p = arcs;
displayTwoDimArray(p);
//递归求出具有m条边的最小权值
for (int m = 2; m < vexnum; m++)
{
int **Lm;
Lm = externShortestPaths(p, arcs);
p = Lm;
displayTwoDimArray(p);
}
return p;
}
//通过使用重复平方来计算矩阵
int** fastAllPairsShortestPaths()
{
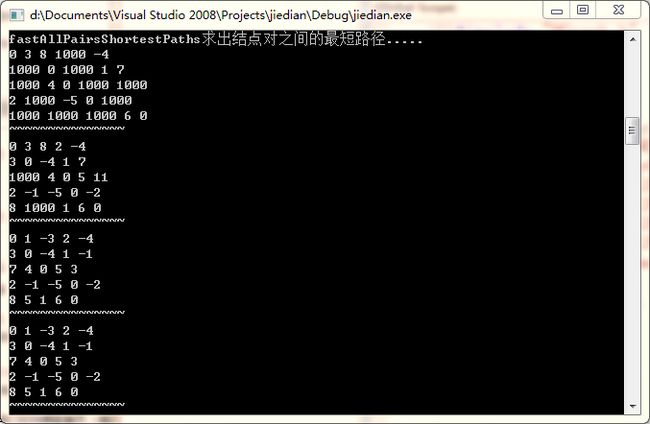
cout << "fastAllPairsShortestPaths求出结点对之间的最短路径....." << endl;
int **p; //指向前一个二维数组
p = arcs;
displayTwoDimArray(p);
//递归求出具有m条边的最小权值
for (int m = 2; m < vexnum; m++)
{
int **Lm;
Lm = externShortestPaths(p, p);
p = Lm;
displayTwoDimArray(p);
}
return p;
}
/*************************************************************************
Floyed算法:
dk[i][j]:从结点i到结点j的所有中间结点全部取自于集合{1,2....k}的一条最短路径的权重
arcs[i][j] if k == 0
dk[i][j] =
min(d(k-1)[i][j], d(k-1)[i][k] + d(k-1)[k][j]) if (k >= 1)
矩阵Dn = (d(n)[i][j])即为最后的答案
关于pi的求法:
if k == 0
NULL if i = j | arcs[i][j] = INFINITE
pi(0) =
i if i != j && arcs[i][j] != INFINITE
if k >= 1
pi(k-1)[i][j] if d(k-1)[i][j] <= d(k-1)[i][k] + d(k-1)[k][j]
pi(k)[i][j] =
pi(k-1)[k][j] if d(k-1)[i][j] > d(k-1)[i][k] + d(k-1)[k][j]
**************************************************************************/
int** FloydWarshall()
{
int i, j, k;
int **p = arcs;
/*int **parr[SIZE+1];*/
/*parr[0] = p;*/
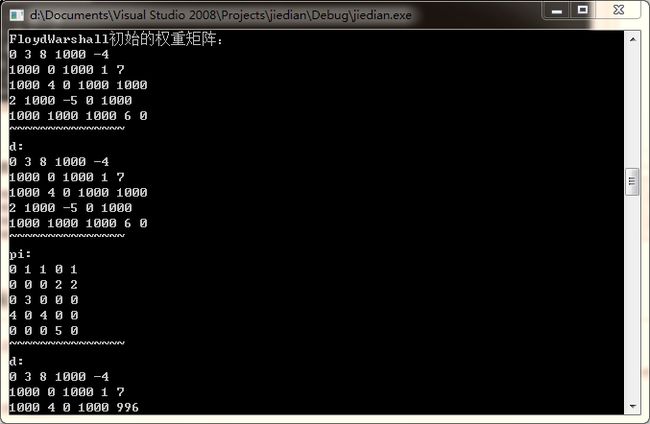
cout << "FloydWarshall初始的权重矩阵:" << endl;
displayTwoDimArray(p);
int **pi = new int *[SIZE];
for (i = 0; i < SIZE; i++)
{
pi[i] = new int[SIZE];
}
//当k == 0时,初试化pi(0)
for (i = 0; i < SIZE; i++)
{
for (j = 0; j < SIZE; j++)
{
if (i == j || arcs[i][j] == INFINITE)
pi[i][j] = NULL;
else
pi[i][j] = i+1;
}
}
cout << "d:" << endl;
displayTwoDimArray(p);
cout << "pi:" << endl;
displayTwoDimArray(pi);
for (k = 1; k <= SIZE; k++)
{
//构造D[k]和Pi[k]
int **dk = new int *[SIZE];
for (i = 0; i < SIZE; i++)
dk[i] = new int[SIZE];
int **pii = new int *[SIZE];
for (i = 0; i < SIZE; i++)
pii[i] = new int[SIZE];
for (i = 0; i < SIZE; i++)
{
for (j = 0; j < SIZE; j++)
{
if (p[i][j] <= p[i][k-1] + p[k-1][j])
{
dk[i][j] = p[i][j];
pii[i][j] = pi[i][j];
}
else
{
dk[i][j] = p[i][k-1] + p[k-1][j];
pii[i][j] = pi[k-1][j];
}
}
}
/*parr[k] = dk;*/
p = dk;
pi = pii;
cout << "d:" << endl;
displayTwoDimArray(p);
cout << "pi:" << endl;
displayTwoDimArray(pi);
}
return p;
}
//输出一个二维数组
void displayTwoDimArray(int **p)
{
for (int i = 0; i < SIZE; i++)
{
for (int j = 0; j < SIZE; j++)
cout << p[i][j] << " ";
cout << endl;
}
cout << "~~~~~~~~~~~~~~~" << endl;
}
/*******************************************************************
不带返回值的结点对最短路径算法,二维数组是直接定义,属于局部定义,而要求
的矩阵也都是通过参数传递,而不是返回值,因为返回值不能返回一个局部的数组
*******************************************************************/
void externShortestPaths1(int (*L)[SIZE], int (*Lnext)[SIZE], int (*W)[SIZE])
{
//Lnext数组, 根据L和arcs来计算出Lnext, 在L的基础上再多加一条边
for (int i = 0; i < vexnum; i++)
{
for (int j = 0; j < vexnum; j++)
{
if (i == j)
Lnext[i][j] = 0;
else
Lnext[i][j] = INFINITE;
for (int k = 0; k < vexnum; k++)
{
//Lnext[i][j]的值为L[i][k]每次加上一条边的权重的最小值
// 0 < k < vexnum,相当于将所有的边都加到原来的最小值上过一遍。
if (L[i][k] + W[k][j] < Lnext[i][j])
Lnext[i][j] = L[i][k] + W[k][j];
}
}
}
}
void slowAllPairsShortestPaths1()
{
cout << "slowAllPairsShortestPaths1求出结点对之间的最短路径....." << endl;
int (*p)[SIZE];
int L1[SIZE][SIZE];
for (int i = 0; i < vexnum; i++)
for (int j = 0; j < vexnum; j++)
L1[i][j] = arcs[i][j];
p = L1;
displayTwoDimArray1(p);
//递归求出具有m条边的最小权值
for (int m = 2; m < vexnum; m++)
{
int Lm[SIZE][SIZE];
externShortestPaths1(p, Lm, L1);
p = Lm;
displayTwoDimArray1(p);
}
}
void fastAllPairsShortestPaths1()
{
cout << "fastAllPairsShortestPaths1求出结点对之间的最短路径....." << endl;
int (*p)[SIZE];
int L1[SIZE][SIZE];
for (int i = 0; i < vexnum; i++)
for (int j = 0; j < vexnum; j++)
L1[i][j] = arcs[i][j];
p = L1;
displayTwoDimArray1(p);
//递归求出具有m条边的最小权值
for (int m = 1; m < vexnum-1; m *= 2)
{
int Lm[SIZE][SIZE];
externShortestPaths1(p, Lm, p);
p = Lm;
displayTwoDimArray1(Lm);
}
}
//输出一个二维数组,参数为指向二维数组的指针
void displayTwoDimArray1(int (*p)[SIZE])
{
for (int i = 0; i < SIZE; i++)
{
for (int j = 0; j < SIZE; j++)
cout << p[i][j] << " ";
cout << endl;
}
cout << "~~~~~~~~~~~~~~~" << endl;
}
private:
static const int INFINITE = 1000; //如果两个顶点之间可不达,则为该值
VertexType *vvec; //顶点向量
int **arcs; //邻接矩阵, 存放顶点关系,对带权图,为边权值
//对于无权图,用1或0表示,表示相邻与否;
int vexnum; //图的当前顶点个数
int arcnum; //图的弧数
GraphKind kind; //图的种类标志
//const int SIZE; //邻接矩阵的维度
};
#endif
#include "MGraph.h"
int main()
{
MGraph wdgGraph(5, WDG);
wdgGraph.CreateWDG1();
wdgGraph.displayGraph();
wdgGraph.slowAllPairsShortestPaths();
wdgGraph.slowAllPairsShortestPaths1();
wdgGraph.fastAllPairsShortestPaths();
wdgGraph.fastAllPairsShortestPaths1();
wdgGraph.FloydWarshall();
system("pause");
return 0;
} 运行结果为:没有全部截取,因为两个slow,两个fast中间运行结果是一样的,floyd太长了。。。截了一点,实际运行结果贴书上图。。。
Floyd运行图: