4.2《算法图解》笔记——Chapter 7 Dijkastra Algorithm
算法图解笔记——Chapter 7 Dijkastra Algorithm
Author: Seven Zou
Email: [email protected]
Language: Python2.7
7 狄克斯特拉算法
在昨天学到的了广度优先搜索,可以很好地解决最短路径问题。但如果加入时间变量问题——寻找最快的路径,就可以引入今天所学的另一种图算法——狄克斯特拉算法(Dijkstra’s Algorithm)。
7.1 算法的使用
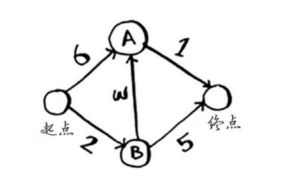
这里有如上图关系,数字表示的是时间(min)。找出从起点到终点耗时最短的路径,使用狄克斯特拉算法需要如下步骤。
- 1.找出“最便宜”的节点,即可在最短时间内到达的节点;
- 2.更新该节点的邻居的开销,其含义将稍后叙述;
- 3.重复这个过程,直到对图中的每个节点都这样做;
- 4.计算最终路径。
1.找出“最便宜”的节点。从起点开始,当前状态只能获取两条信息,通往A和B的时间,且通往B的时间更短仅为2分钟。对于终点,假设为 ∞ \infty ∞。
| 节点 | 耗时 |
|---|---|
| A | 6 |
| B | 2 |
| 终点 | ∞ \infty ∞ |
2.计算经节点B通过各个邻居的时间。
| 节点 | 耗时 |
|---|---|
| 起点->B | 2 |
| 起点->B->A | 2+3=5 |
| 起点->B->终点 | 2+5=7 |
此时的时间就可以得到更新,因为获得时间出现了更优的值。
- 前往节点A的更短路径(“起点 -> B -> A” 耗时少于 “起点 -> A”)
- 前往终点的更短路径(耗时" ∞ \infty ∞" -> “7”)
3.重复。刚刚针对B进行了操作,本步骤继续对A节点进行同样操作。结果发现前往终点的时间更新为6分钟。
| 节点 | 耗时 |
|---|---|
| 起点->A | 6 |
| 起点->A->终点 | 6+1=7 |
| 起点->B->A->终点 | 2+3+1=6 |
此时,对每个节点都运行了狄克斯特拉算法,重新更新前往各节点的耗时数据所以第一个表格数据更新为如下。
| 节点 | 耗时 |
|---|---|
| A | 5 |
| B | 2 |
| 终点 | 6 |
4.最后,计算最终路径。
对于最短路径的概念,在广度优先搜索中,意义是段数最少。而在狄克斯特拉算法中,相当于你给每段都分配了一个数字(权重),所以算法最终是找出总权重最小的路径。现在对狄克斯特拉算法应该有了大概的认知,下面来详细介绍其中的细节知识。
7.2 术语
狄克斯特拉算法用于每条边都有关联数字的图,这些数字称为权重(weight)。因此有,带权重的图称为加权图(weighted graph),不带权重的图称为非加权图(unweighted graph)。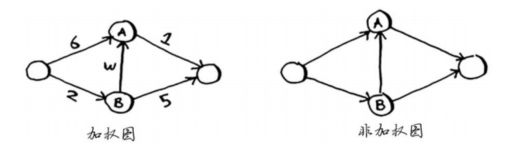
针对非加权图,广度优先搜索是适用的,而要计算加权图的最短路径,可使用狄克斯特拉算法。图中可以还存在环,意味着可从一个节点出发,走了一圈后又回到这个节点。对于路径中,存在环,可以选择绕过,也可以选择包含环的路径并且你可以选择绕环多次,但每绕环一次,权重会增加一次。
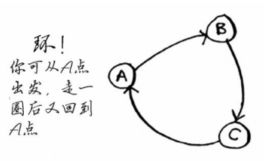
看了上述的环结构,来回顾一下第六章的有向图,无向图。无向图中两个节点互相指向对方,这就是环。在无向图中,每条边都是一个环,所以狄克斯特拉算法只适用于有向无环图(directed acyclic graph,DAG)。
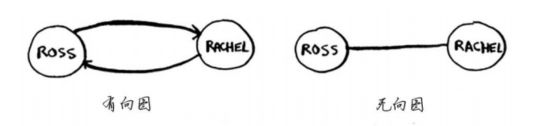
7.3 案例
起初Rama想拿一本乐谱来换架钢琴。Alex说愿意拿他最喜欢乐队的海报来换乐谱,如果再加$5,还可拿乐谱换稀有的黑胶唱片。Amy说她愿意拿吉他或架子鼓来换这张海报或者黑胶唱片。Beethoven说他一直想要吉他,他愿意拿钢琴换Amy的吉他或架子鼓。那么这几人的置换关系可由下图确定。
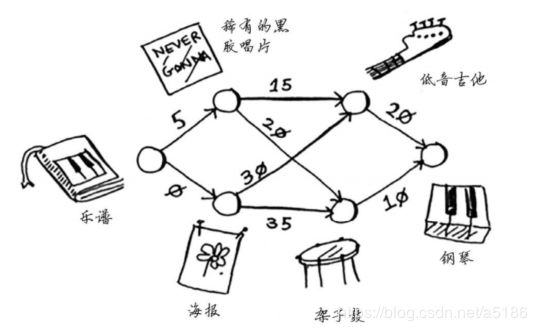
图中节点表示大家愿意拿出置换的物品,权重为交换时需要额外加的金额。其最终目的为Rama需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。此种情况可使用狄克斯特拉算法。首先创建列表,由起点开始到达各节点的数值(权重)(不知如何到达的节点仍取 ∞ \infty ∞),在执行算法过程中,不断更新此列表,并需在表中添加父节点的列。
| 节点 | 开销 | 父节点 |
|---|---|---|
| 黑胶唱片 | 5 | 乐谱 |
| 海报 | 0 | 乐谱 |
| 吉他 | ∞ \infty ∞ | —— |
| 架子鼓 | ∞ \infty ∞ | —— |
| 钢琴 | ∞ \infty ∞ | —— |
1.找出最便宜的点。由图中可知,换海报是最便宜的路径,需要支付的额外费用最少。
2.计算前往该节点的各个邻居的开销。那么就有
| 父节点 | 节点 | 开销 |
|---|---|---|
| 乐谱 | 黑胶唱片 | 5 |
| 乐谱 | 海报 | 0 |
| 海报 | 吉他 | 0+30=30 |
| 海报 | 架子鼓 | 0+35=35 |
| —— | 钢琴 | ∞ \infty ∞ |
再执行第一步,下一个最便宜的节点是黑胶唱片。
再执行第二部,更新黑胶唱片的各个邻居的开销。
| 父节点 | 节点 | 开销 |
|---|---|---|
| 乐谱 | 黑胶唱片 | 5 |
| 乐谱 | 海报 | 0 |
| 黑胶唱片 | 吉他 | 5+15=20 |
| 黑胶唱片 | 架子鼓 | 5+20=25 |
| —— | 钢琴 | ∞ \infty ∞ |
此时更新了对架子鼓和吉他的开销,发现经“黑胶唱片”节点开销更低,因此父节点改为黑胶唱片。下一个最便宜的是吉他,因此再次更新其邻居的开销。
| 父节点 | 节点 | 开销 |
|---|---|---|
| 乐谱 | 黑胶唱片 | 5 |
| 乐谱 | 海报 | 0 |
| 黑胶唱片 | 吉他 | 5+15=20 |
| 黑胶唱片 | 架子鼓 | 5+20=25 |
| 吉他 | 钢琴 | 5+15+20=40 |
再对架子鼓进行更新。
| 父节点 | 节点 | 开销 |
|---|---|---|
| 乐谱 | 黑胶唱片 | 5 |
| 乐谱 | 海报 | 0 |
| 黑胶唱片 | 吉他 | 5+15=20 |
| 黑胶唱片 | 架子鼓 | 5+20=25 |
| 架子鼓 | 钢琴 | 5+20+10=35 |
因此,得到最便宜的路径时,Rama需要额外支付$35。而如何确定路径,来根据父节点逆向判断。(钢琴 -> 架子鼓 -> 黑胶唱片) 显然,Rama需要用乐谱来换黑胶唱片。在本章对最短路径的理解,不再停留字面意思:计算两点或两人之间的最短路径,最短路径指的也可能让某种度量指标最小。
7.4 负权边情况
还是针对上述案例,如果黑胶唱片不是Alex的,而是Sarah的,且Sarah愿意用黑胶唱片和$7换海报。那么对于Rama,换得海报后,再与Sarah交换不仅不用支付费用还可获得$7。
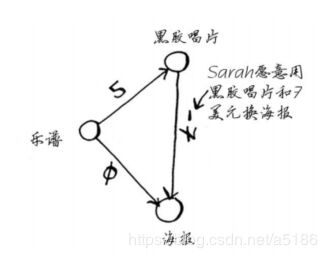
在图中,黑胶唱片 -> 海报 边得权重为 -7。那么Rama就两种获得海报的方式有两种,并且显然第二种更划算,那么海报换架子鼓也存在两种方式。
| 方式1 | 方式2 |
|---|---|
| 乐谱 -> 海报 | 乐谱 -> 黑胶唱片 -> 海报 ($2) |
| 乐谱 -> 海报 -> 架子鼓($35) | 乐谱 -> 黑胶唱片 -> 海报 -> 架子鼓($33) |
但实际上,狄克斯特拉不能处理包含负权边的图。在包含负权边的图种,要找出最短路径,可以使用另外一种算法——贝尔曼-福德算法(Bellman-Ford Algorithm)。
7.5 算法实现
案例为如下图
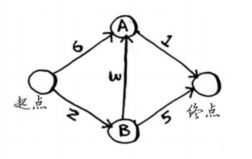
编写这个代码,需要三个散列表。

随着算法的执行,不断更新列表costs和parents。
graph = {}
graph["astart"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
# 因此graph["start"]是一个散列表,要获取起点的所有邻居可用print
print graph["start"].keys()
Output: ['a', 'b']
针对其他节点及其邻居进行添加
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {} # 终点没有任何邻居
还需要一个散列表来存储每个节点得开销。
infinity = float("inf") # python中表示无穷大
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
还需要一个存储父节点得散列表
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = "None"
最后,记录处理过得节点。对于同一个节点,不用处理多次。
processed = []
整理后有
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
for node in costs: # 遍历所有的节点
cost = costs[node]
if cost < lowest_cost and node not in processed: # 如果当前节点的开销更低且未处理过
lowest_cost = cost # 就将其视为开销最低的节点
lowest_cost_node = node
return lowest_cost_node
node = find_lowest_cost_node(costs) # 在未处理得节点中找出开销最小得节点
while node is not None: # 在所有节点都被处理过后结束
cost = costs[node]
neighbors = graph[node]
for n in neighbors.keys(): # 遍历当前节点的所有邻居
new_cost = cost + neighbors[n]
if costs[n] > new_cost: # 如果经当前节点前往该邻居更近
costs[n] = new_cost # 就更新该邻居的开销
parents[n] = node # 同时将该邻居的父节点设置为当前节点
processed.append(node) # 将当前节点标记为处理过
node = find_lowest_cost_node(costs) # 找出接下来要处理的节点,并循环
| 算法 | 适用图的种类查找最短路径 |
|---|---|
| 广度优先搜索 | 非加权图 |
| 狄克斯特拉算法 | 加权图(权重为正) |
| 贝尔曼-福德算法 | 加权图( 包含负权边) |
Reference
[美]Aditya Bhargava/袁国忠, 算法图解, 北京:人民邮电出版社, 2017.3.
附个人Github地址: https://github.com/shiqi0404/Algorithm_Diagram,其中包括笔记、Code还有书本pdf版。