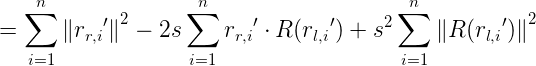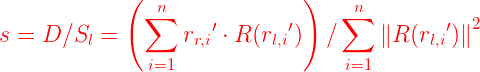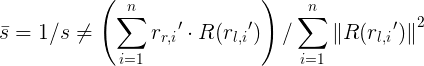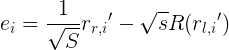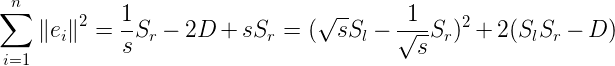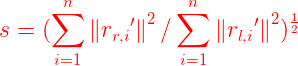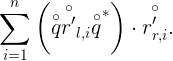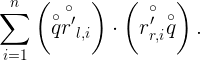ORB-SLAM2代码阅读笔记(十):sim3求解
Table of Contents
1.sim3的简单概述
2.sim3算法介绍
1)3对匹配的3D点建立坐标系
2)旋转矩阵计算
3)平移向量计算
4)尺度计算
3.代码解析
1)sim3求解器构造函数Sim3Solver
2)sim3迭代求解Sim3Solver::iterate
本篇笔记对 ORB-SLAM2代码阅读笔记(八):LoopClosing线程 中提到的sim3进行了分析,以熟悉使用三对匹配点求解位姿变换的方法。
1.sim3的简单概述
sim3简单来说,就是使用3对匹配点来进行相似变换(similarity transformation)的求解,进而解出两个坐标系之间的旋转矩阵、平移向量和尺度。ORB-SLAM2中使用的sim3求解方法来自 Horn 1987, Closed-form solution of absolute orientation using unit quaternions 这篇论文。所以,需要了解一下这篇论文中提出的求解思想,以帮助理解代码。
ORB-SLAM2系统在LoopClosing线程中,当检测到闭环候选帧的时候,就需要对当前关键帧和对应的闭环候选帧之间计算其变换关系。这时需要用当前关键帧和其对应的闭环候选帧进行sim3求解,这里的sim3求解是对当前关键帧和闭环候选帧之间匹配的MapPoint进行sim3求解。通过sim3变换解出当前关键帧和闭环候选帧的匹配MapPoint之间的旋转矩阵R、平移向量t、尺度变换s,也就得到了当前关键帧到闭环关键帧之间的sim3变换gScm。使用这个sim3变换gScm乘上闭环关键帧的sim3位姿gSmw,mg2oScw=gScm*gSmw的乘积mg2oScw就是当前关键帧的sim3位姿,之后在闭环校正中就可以使用这个sim3位姿转换为SE3位姿后对当前关键帧进行位姿校正(当然也要对关键帧对应的MapPoints以及其共视的关键帧进行校正)。当然在实际代码中,这个过程还要做多次投影和优化操作以确保更高的准确率和精度,这个可以阅读ORB-SLAM2该部分的代码来体会。
以下图为例,A为当前关键帧,B为候选关键帧。
当相机从B处开始运动到A处的时候,检测到B为A的闭环候选帧。此时,考虑到相机从B运动到A的过程中不光会产生旋转和平移的误差,同时也会产生尺度漂移的累积,需要计算A和B之间的sim3变换,来找到A和B之间的sim3变换(包括旋转矩阵R、平移向量t、尺度变换s),有了这些值之后,就可以对关键帧A的位姿进行纠正。
2.sim3算法介绍
Closed-form solution of absolute orientation using unit quaternions论文提供了一种算法,通过两个坐标系之间3对匹配点来确定两个坐标系之间的变换关系。
1)3对匹配的3D点建立坐标系
如上图所示,在左右两个坐标系中各有3个点,左侧三个点分别是![]() ,
,![]() ,
,![]() ,右侧三个点为
,右侧三个点为![]() ,
,![]() ,
,![]() 。
。
可以看出,左侧的![]() 和右侧的
和右侧的![]() 都处于坐标系的原点处,则我们可以计算出在X轴、Y轴和Z轴上的单位向量如下:
都处于坐标系的原点处,则我们可以计算出在X轴、Y轴和Z轴上的单位向量如下:
X轴:x轴上的向量为![]() ,对
,对![]() 除以其模长得到在x轴方向上的单位向量
除以其模长得到在x轴方向上的单位向量![]()
图中这种情况下![]() 为原点,
为原点,![]() 在x轴方向上,所以两个点相减后所得向量在x轴上,对向量除以模长就是x轴上的单位向量。
在x轴方向上,所以两个点相减后所得向量在x轴上,对向量除以模长就是x轴上的单位向量。
Y轴:y轴上的向量为![]() ,对
,对![]() 除以
除以![]() 的模长得到y轴方向上的单位向量
的模长得到y轴方向上的单位向量![]()
![]() 所得为从
所得为从![]() 到
到![]() 这两个点之间的向量,
这两个点之间的向量,![]() 表示向量在x轴方向上的单位长度,
表示向量在x轴方向上的单位长度,![]() 表示该向量在x轴方向上的向量的长度。则向量减去其在x轴方向的向量就得到了在y轴方向上的向量。
表示该向量在x轴方向上的向量的长度。则向量减去其在x轴方向的向量就得到了在y轴方向上的向量。
Z轴:由于z轴垂直与x轴和y轴,所以z轴所在方向也就是x和y轴方向向量叉乘乘积的方向(两个向量叉乘后的乘积所在的向量方向和这两个向量垂直),则z轴方向上的单位向量为![]()
同理,也可推出右侧坐标系各个轴上的单位向量![]() 。
。
2)旋转矩阵计算
根据1)中所得的坐标系单位向量,可以得到左右两侧坐标系的各个方向单位向量构成的矩阵:![]() ,
,![]()
此时,如果左侧坐标系中有一个向量![]() ,则
,则![]() 可以计算结果为
可以计算结果为![]() 在三个坐标轴方向上的向量值。
在三个坐标轴方向上的向量值。![]() 左乘
左乘![]() 后所得结果为变换到右侧坐标系中的向量
后所得结果为变换到右侧坐标系中的向量![]() 。
。
则可以推导出从左侧坐标系旋转到右侧坐标系中的旋转矩阵为:![]()
3)平移向量计算
假设左右坐标系中各有![]() 各点,他们在左右两侧坐标系中的测量坐标值为
各点,他们在左右两侧坐标系中的测量坐标值为![]() 和
和![]() ,
,![]() 的取值从1到
的取值从1到![]() 。
。
此时,一个向量从左侧坐标系到右侧坐标系的变换可表示为:![]() 其中,s为尺度变换,
其中,s为尺度变换,![]() 为平移偏移量。
为平移偏移量。![]() 表示
表示![]() 的旋转。
的旋转。
实际当中,两个坐标系之间的变换不会那么容易计算出精确的变换向量,和机器学习中采用方法相同,都是采用优化的方法(最小化误差的方法)来求解的,也就是使用最小二乘法来求解。此时,容易看出这里的误差为:
![]()
那么,求解的最小二乘问题变成了求解:
那么,怎么来求解这个最小误差呢?我们先把要求解的表达式放在这里。这里我们要求解的是平移向量,也就是上边的![]() 。看看作者是怎么引入问题求解方法的。
。看看作者是怎么引入问题求解方法的。
计算左侧和右侧坐标系中所有点的质心(其实也就是所有点的中心):
则每一个点距离质心的距离为:
![]()
![]()
根据上边得出的变换公式可得:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
此时,优化函数如下:
此时剩下第一部分和第三部分,第一部分和![]() 没关系,第三部分不可能为负值。所以,优化函数在
没关系,第三部分不可能为负值。所以,优化函数在![]() 的情况下取得最小值。
的情况下取得最小值。
带入上式:![]() 中,可得平移向量
中,可得平移向量![]() :
:
![]()
4)尺度计算
由于![]() ,所以可得误差函数:
,所以可得误差函数:
我们进一步可以把这个形式写成如下形式:
![]()
此时,要是误差取最小值,则必须第一项为0,此时
根据对称性可得:![]()
![]()
我们期望计算出来的值为:![]()
![]()
当已知两个系统中的一个系统的坐标比另一个系统的坐标精度高得多时,上述两个不对称结果中的一个可能是合适的。
如果两组测量中的误差相似,则对误差项使用对称表达式更为合理:
这种对称结果的一个有点是,它允许人们在不需要知道旋转的情况下确定尺度。重要的是,旋转的确定不受我们选择比例因子的三个值之一的影响。在每种情况下,当D尽可能大时,误差能取得最小值。也就是说,我们必须选择使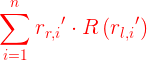 尽可能大的旋转值。
尽可能大的旋转值。
注意:这里的意思是说,只有在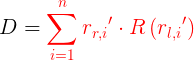 取得最大值的情况下,误差才会最小,所以为了求得最小误差,我们应该去求最大的
取得最大值的情况下,误差才会最小,所以为了求得最小误差,我们应该去求最大的![]() .
.
现在,我们把问题变成了求最大的![]() 。
。
旋转可以使用多种方式进行表达,此处,引入了四元数来表达。
一个四元数表达如下:![]()
![]()
其中![]() 为实部,并且满足:
为实部,并且满足:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
此时两个四元数的点乘积为:![]()
定义![]() 的共轭向量为:
的共轭向量为:![]()
可以用单位四元数表达为如下形式:
此时,假设![]()
![]()
定义了M就是为了用其中的元素来表示N,N定义如下:
此时,对N矩阵进行特征值分解求解最大特征值,该特征值对应的特征向量就是待求的四元数。
根据四元数可以求出旋转矩阵R、平移向量t和尺度s。
3.代码解析
在Closed-form solution of absolute orientation using unit quaternions这篇论文的结论部分,作者坦言该论文中的算法表达相对复杂一些,但是好处是一些程序库中已经实现了该算法的sim3求解,所以对我们使用者来说,只要调用库函数就行了,这样就简单了好多。
ORB-SLAM2中sim3求解流程相关代码位于LoopClosing::ComputeSim3()中。主要的求解函数如下:
1)sim3求解器构造函数Sim3Solver
Sim3Solver函数用于针对每一个和当前关键帧存在闭环关系的闭环候选关键帧之间构造sim3求解器。求解器中,主要是确定两个关键帧中匹配的MapPoint的对应关系,构造好匹配的MapPoint点对列表,并设置Ransac相关参数用于后续iterate中求解使用。
Sim3Solver::Sim3Solver(KeyFrame *pKF1, KeyFrame *pKF2, const vector &vpMatched12, const bool bFixScale):
mnIterations(0), mnBestInliers(0), mbFixScale(bFixScale)
{
mpKF1 = pKF1;
mpKF2 = pKF2;
vector vpKeyFrameMP1 = pKF1->GetMapPointMatches();
mN1 = vpMatched12.size();
mvpMapPoints1.reserve(mN1);
mvpMapPoints2.reserve(mN1);
mvpMatches12 = vpMatched12;
mvnIndices1.reserve(mN1);
mvX3Dc1.reserve(mN1);
mvX3Dc2.reserve(mN1);
cv::Mat Rcw1 = pKF1->GetRotation();
cv::Mat tcw1 = pKF1->GetTranslation();
cv::Mat Rcw2 = pKF2->GetRotation();
cv::Mat tcw2 = pKF2->GetTranslation();
mvAllIndices.reserve(mN1);
size_t idx=0;
for(int i1=0; i1isBad() || pMP2->isBad())
continue;
//获取MapPoint中记录的能看到该MapPoint的keyframe中对应的关键点的index
int indexKF1 = pMP1->GetIndexInKeyFrame(pKF1);
int indexKF2 = pMP2->GetIndexInKeyFrame(pKF2);
if(indexKF1<0 || indexKF2<0)
continue;
const cv::KeyPoint &kp1 = pKF1->mvKeysUn[indexKF1];
const cv::KeyPoint &kp2 = pKF2->mvKeysUn[indexKF2];
const float sigmaSquare1 = pKF1->mvLevelSigma2[kp1.octave];
const float sigmaSquare2 = pKF2->mvLevelSigma2[kp2.octave];
mvnMaxError1.push_back(9.210*sigmaSquare1);
mvnMaxError2.push_back(9.210*sigmaSquare2);
mvpMapPoints1.push_back(pMP1);
mvpMapPoints2.push_back(pMP2);
mvnIndices1.push_back(i1);
//pMP1对应的相机坐标
cv::Mat X3D1w = pMP1->GetWorldPos();
mvX3Dc1.push_back(Rcw1*X3D1w+tcw1);
cv::Mat X3D2w = pMP2->GetWorldPos();
//pMP2对应的相机坐标
mvX3Dc2.push_back(Rcw2*X3D2w+tcw2);
mvAllIndices.push_back(idx);
idx++;
}
}
//相机内参
mK1 = pKF1->mK;
mK2 = pKF2->mK;
//FromCameraToImage函数计算从相机坐标到像素坐标的投影点,mvP1im1为投影点列表。
FromCameraToImage(mvX3Dc1,mvP1im1,mK1);
FromCameraToImage(mvX3Dc2,mvP2im2,mK2);
SetRansacParameters();
} 其中调用的函数FromCameraToImage代码如下:
/**
* 计算从相机坐标到像素坐标的投影
*/
void Sim3Solver::FromCameraToImage(const vector &vP3Dc, vector &vP2D, cv::Mat K)
{
const float &fx = K.at(0,0);
const float &fy = K.at(1,1);
const float &cx = K.at(0,2);
const float &cy = K.at(1,2);
vP2D.clear();
//vP3Dc为相机坐标,vP2D为要投影到的像素点坐标
vP2D.reserve(vP3Dc.size());
for(size_t i=0, iend=vP3Dc.size(); i(2));
const float x = vP3Dc[i].at(0)*invz;
const float y = vP3Dc[i].at(1)*invz;
vP2D.push_back((cv::Mat_(2,1) << fx*x+cx, fy*y+cy));
}
} 2)sim3迭代求解Sim3Solver::iterate
iterate函数是开始进行sim3求解的函数。遍历1)中构造好的每个求解器,调用求解器中的iterate函数进行求解。ORB-SLAM2中迭代5次进行求解。
cv::Mat Sim3Solver::iterate(int nIterations, bool &bNoMore, vector &vbInliers, int &nInliers)
{
bNoMore = false;
vbInliers = vector(mN1,false);
nInliers=0;
if(N vAvailableIndices;
cv::Mat P3Dc1i(3,3,CV_32F);
cv::Mat P3Dc2i(3,3,CV_32F);
int nCurrentIterations = 0;
while(mnIterations=mnBestInliers)
{
mvbBestInliers = mvbInliersi;
mnBestInliers = mnInliersi;
mBestT12 = mT12i.clone();
mBestRotation = mR12i.clone();
mBestTranslation = mt12i.clone();
mBestScale = ms12i;
if(mnInliersi>mRansacMinInliers)
{
nInliers = mnInliersi;
for(int i=0; i=mRansacMaxIts)
bNoMore=true;
return cv::Mat();
} /**
* 计算sim3
*/
void Sim3Solver::ComputeSim3(cv::Mat &P1, cv::Mat &P2)
{
// Custom implementation of:
// Horn 1987, Closed-form solution of absolute orientataion using unit quaternions
// Step 1: Centroid and relative coordinates
cv::Mat Pr1(P1.size(),P1.type()); // Relative coordinates to centroid (set 1)
cv::Mat Pr2(P2.size(),P2.type()); // Relative coordinates to centroid (set 2)
cv::Mat O1(3,1,Pr1.type()); // Centroid of P1
cv::Mat O2(3,1,Pr2.type()); // Centroid of P2
ComputeCentroid(P1,Pr1,O1);
ComputeCentroid(P2,Pr2,O2);
// Step 2: Compute M matrix
cv::Mat M = Pr2*Pr1.t();
// Step 3: Compute N matrix
double N11, N12, N13, N14, N22, N23, N24, N33, N34, N44;
cv::Mat N(4,4,P1.type());
N11 = M.at(0,0)+M.at(1,1)+M.at(2,2);
N12 = M.at(1,2)-M.at(2,1);
N13 = M.at(2,0)-M.at(0,2);
N14 = M.at(0,1)-M.at(1,0);
N22 = M.at(0,0)-M.at(1,1)-M.at(2,2);
N23 = M.at(0,1)+M.at(1,0);
N24 = M.at(2,0)+M.at(0,2);
N33 = -M.at(0,0)+M.at(1,1)-M.at(2,2);
N34 = M.at(1,2)+M.at(2,1);
N44 = -M.at(0,0)-M.at(1,1)+M.at(2,2);
N = (cv::Mat_(4,4) << N11, N12, N13, N14,
N12, N22, N23, N24,
N13, N23, N33, N34,
N14, N24, N34, N44);
// Step 4: Eigenvector of the highest eigenvalue
cv::Mat eval, evec;
cv::eigen(N,eval,evec); //evec[0] is the quaternion of the desired rotation
cv::Mat vec(1,3,evec.type());
(evec.row(0).colRange(1,4)).copyTo(vec); //extract imaginary part of the quaternion (sin*axis)
// Rotation angle. sin is the norm of the imaginary part, cos is the real part
double ang=atan2(norm(vec),evec.at(0,0));
vec = 2*ang*vec/norm(vec); //Angle-axis representation. quaternion angle is the half
mR12i.create(3,3,P1.type());
cv::Rodrigues(vec,mR12i); // computes the rotation matrix from angle-axis
// Step 5: Rotate set 2
cv::Mat P3 = mR12i*Pr2;
// Step 6: Scale
if(!mbFixScale)
{
double nom = Pr1.dot(P3);
cv::Mat aux_P3(P3.size(),P3.type());
aux_P3=P3;
cv::pow(P3,2,aux_P3);
double den = 0;
for(int i=0; i(i,j);
}
}
ms12i = nom/den;
}
else
ms12i = 1.0f;
// Step 7: Translation
mt12i.create(1,3,P1.type());
mt12i = O1 - ms12i*mR12i*O2;
// Step 8: Transformation
// Step 8.1 T12
mT12i = cv::Mat::eye(4,4,P1.type());
cv::Mat sR = ms12i*mR12i;
sR.copyTo(mT12i.rowRange(0,3).colRange(0,3));
mt12i.copyTo(mT12i.rowRange(0,3).col(3));
// Step 8.2 T21
mT21i = cv::Mat::eye(4,4,P1.type());
cv::Mat sRinv = (1.0/ms12i)*mR12i.t();
sRinv.copyTo(mT21i.rowRange(0,3).colRange(0,3));
cv::Mat tinv = -sRinv*mt12i;
tinv.copyTo(mT21i.rowRange(0,3).col(3));
}


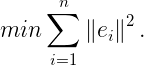



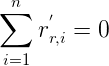
![\large \sum _{i=1}^{n}\left \| e_i \right \|^2=\sum _{i=1}^n\left \| {r_{r,i}}'-\left [ sR({r_{l,i}}')+{r_0}' \right ] \right \|^2](http://img.e-com-net.com/image/info8/3040a2c7630a478391f48916675a4c9a.gif)
![\large 2{r_0}'\cdot \sum _{i=1}^{n}\left [ {r_{r,i}}'-sR({r_{l,i}}') \right ]=0](http://img.e-com-net.com/image/info8/8c2009e114734c3dbd61391f1c8ae25a.gif)
![\large =\sum _{i=1}^n\left \| {r_{r,i}}'-\left [ sR({r_{l,i}}') \right ] \right \|^2](http://img.e-com-net.com/image/info8/ef747e046441419d94fd865eaa71b574.gif)