Verilog设计实例（5）详解全类别加法器（二）

---

写在前面

相关博文

个人博客首页

---

正文

超前进位加法器

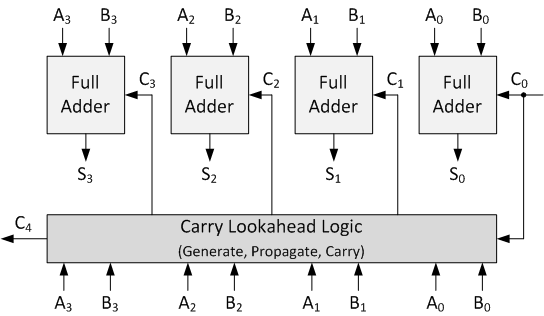
超前加法器由许多级联在一起的全加法器组成。 它仅通过简单的逻辑门就可以将两个二进制数相加。 下图显示了连接在一起以产生4位超前进位加法器的4个全加器。 超前进位加法器类似于纹波提前加法器。 不同之处在于，超前进位加法器能够在完全加法器完成其运算之前计算进位。 这比起波纹加法器具有优势，因为它能够更快地将两个数字加在一起。 缺点是需要更多逻辑。 您会发现在设计FPGA和ASIC时，执行速度和使用的资源之间通常会达到平衡。

所谓超前进位，就是在加法运算得到结果之前，得到进位，如何判断是否进位呢？
以上图为例给出三步判断：

1. 如果Ai与Bi都为1，则一定进位，否则不一定进位；由此确定一定进位的情况，可以用与门实现。伪代码表示为：Gi = Ai & Bi;
2. 第一步确定了一定进位的情况，这一步确定可能进位的情况，也就是Ai或Bi有一个1，可以使用或门判断，伪代码为：Pi = Ai | Bi;
3. 这一步进一步确定第二部不确定的情况，如果低一位(进位用Ci表示，则低为可以表示为C_i-1)确定了进位，并且Pi为1，则一定进位，也即Ci = 1。

最后得到进位公式为：

C_(i+1) = G_i | ( P_i & C_i ) ;

由此得到的伪代码为：

  // Create the Generate (G) Terms:  Gi=Ai*Bi
  assign w_G[0] = i_add1[0] & i_add2[0];
  assign w_G[1] = i_add1[1] & i_add2[1];
  assign w_G[2] = i_add1[2] & i_add2[2];
  assign w_G[3] = i_add1[3] & i_add2[3];
 
  // Create the Propagate Terms: Pi=Ai+Bi
  assign w_P[0] = i_add1[0] | i_add2[0];
  assign w_P[1] = i_add1[1] | i_add2[1];
  assign w_P[2] = i_add1[2] | i_add2[2];
  assign w_P[3] = i_add1[3] | i_add2[3];
 
  // Create the Carry Terms:
  assign w_C[0] = 1'b0; // no carry input
  assign w_C[1] = w_G[0] | (w_P[0] & w_C[0]);
  assign w_C[2] = w_G[1] | (w_P[1] & w_C[1]);
  assign w_C[3] = w_G[2] | (w_P[2] & w_C[2]);
  assign w_C[4] = w_G[3] | (w_P[3] & w_C[3]);

4位超前进位加法器

逻辑设计

由上述原理，得到的逻辑设计Verilog代码为：

`timescale 1ns / 1ps
//////////////////////////////////////////////////////////////////////////////////
// Engineer: Reborn Lee
// Module Name: carry_lookahead_adder_4_bit
// Additional Comments:
// https://blog.csdn.net/Reborn_Lee
//////////////////////////////////////////////////////////////////////////////////
`include "full_adder.v"
 
module carry_lookahead_adder_4_bit 
  (
   input [3:0]  i_add1,
   input [3:0]  i_add2,
   output [4:0] o_result
   );
     
  wire [4:0]    w_C;
  wire [3:0]    w_G, w_P, w_SUM;
   
  full_adder full_adder_bit_0
    ( 
      .i_bit1(i_add1[0]),
      .i_bit2(i_add2[0]),
      .i_carry(w_C[0]),
      .o_sum(w_SUM[0]),
      .o_carry()
      );
 
  full_adder full_adder_bit_1
    ( 
      .i_bit1(i_add1[1]),
      .i_bit2(i_add2[1]),
      .i_carry(w_C[1]),
      .o_sum(w_SUM[1]),
      .o_carry()
      );
 
  full_adder full_adder_bit_2
    ( 
      .i_bit1(i_add1[2]),
      .i_bit2(i_add2[2]),
      .i_carry(w_C[2]),
      .o_sum(w_SUM[2]),
      .o_carry()
      );
   
  full_adder full_adder_bit_3
    ( 
      .i_bit1(i_add1[3]),
      .i_bit2(i_add2[3]),
      .i_carry(w_C[3]),
      .o_sum(w_SUM[3]),
      .o_carry()
      );
   
  // Create the Generate (G) Terms:  Gi=Ai*Bi
  assign w_G[0] = i_add1[0] & i_add2[0];
  assign w_G[1] = i_add1[1] & i_add2[1];
  assign w_G[2] = i_add1[2] & i_add2[2];
  assign w_G[3] = i_add1[3] & i_add2[3];
 
  // Create the Propagate Terms: Pi=Ai+Bi
  assign w_P[0] = i_add1[0] | i_add2[0];
  assign w_P[1] = i_add1[1] | i_add2[1];
  assign w_P[2] = i_add1[2] | i_add2[2];
  assign w_P[3] = i_add1[3] | i_add2[3];
 
  // Create the Carry Terms:
  assign w_C[0] = 1'b0; // no carry input
  assign w_C[1] = w_G[0] | (w_P[0] & w_C[0]);
  assign w_C[2] = w_G[1] | (w_P[1] & w_C[1]);
  assign w_C[3] = w_G[2] | (w_P[2] & w_C[2]);
  assign w_C[4] = w_G[3] | (w_P[3] & w_C[3]);
   
  assign o_result = {w_C[4], w_SUM};   // Verilog Concatenation
 
endmodule // carry_lookahead_adder_4_bit

注：头文件中包含的全加器为：

`timescale 1ns / 1ps
//////////////////////////////////////////////////////////////////////////////////
// Engineer: Reborn Lee
// Module Name: full_adder
// https://blog.csdn.net/Reborn_Lee
//////////////////////////////////////////////////////////////////////////////////


module full_adder(
	input  i_bit1,
 	input  i_bit2,
 	input  i_carry,
	output o_sum,
 	output o_carry

    );


	assign o_sum   = i_bit1 ^ i_bit2 ^ i_carry;
        assign o_carry = ((i_bit1 ^ i_bit2) & i_carry) | (i_bit1 & i_bit2);


// More clear method
 
//   wire   w_WIRE_1;
//   wire   w_WIRE_2;
//   wire   w_WIRE_3;
       
//   assign w_WIRE_1 = i_bit1 ^ i_bit2;
//   assign w_WIRE_2 = w_WIRE_1 & i_carry;
//   assign w_WIRE_3 = i_bit1 & i_bit2;
 
//   assign o_sum   = w_WIRE_1 ^ i_carry;
//   assign o_carry = w_WIRE_2 | w_WIRE_3;


  // The third method
 // assign {o_carry, o_sum} = i_bit1 + i_bit2 + i_carry;
 
 

endmodule

功能仿真

`timescale 1ns/1ps
module carry_lookahead_adder_4_bit_tb;

   reg [3:0]  i_add1;
   reg [3:0]  i_add2;
   wire [4:0] o_result;


   initial begin
   	i_add1 = 'd5;
	i_add2 = 'd11;

	# 10
	i_add1 = 'd6;
	i_add2 = 'd15;

	# 10
	i_add1 = 'd11;
	i_add2 = 'd13;

	# 10
	i_add1 = 'd15;
	i_add2 = 'd15;

	#10 $finish;
   end


 // Monitor values of these variables and print them into the log file for debug
   initial
      $monitor ("i_add1 = %b, i_add2 = %b, o_result = %b", i_add1, i_add2, o_result);


   carry_lookahead_adder_4_bit inst_carry_lookahead_adder_4_bit(
   	.i_add1(i_add1),
   	.i_add2(i_add2),
   	.o_result(o_result)
   	);

endmodule

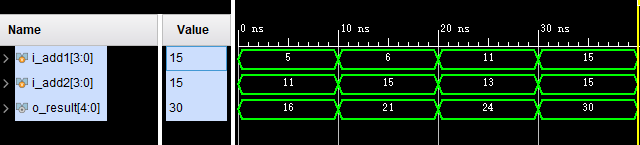
仿真波形及数据

i_add1 = 0101, i_add2 = 1011, o_result = 10000
i_add1 = 0110, i_add2 = 1111, o_result = 10101
i_add1 = 1011, i_add2 = 1101, o_result = 11000
i_add1 = 1111, i_add2 = 1111, o_result = 11110

任意位宽的超前进位加法器

逻辑设计

使用参数化的方式定义位宽为 WIDTH，且使用generate for循环语句来进行全加器例化以及进位产生，设计文件如下：

 
`include "full_adder.v"
 
module carry_lookahead_adder
  #(parameter WIDTH = 3)
  (
   input [WIDTH-1:0] i_add1,
   input [WIDTH-1:0] i_add2,
   output [WIDTH:0]  o_result
   );
     
  wire [WIDTH:0]     w_C;
  wire [WIDTH-1:0]   w_G, w_P, w_SUM;
 
  // Create the Full Adders
  genvar             ii;
  generate
    for (ii=0; ii

• 注意要对第一个进位进行置0，因为第一个全加器没有进位。

功能仿真

功能仿真同上一个tb文件类似，这里不在赘余了。

---

参考资料

• 参考资料1
• 参考资料2

---

交个朋友

• 个人微信公众号：FPGA LAB，左下角二维码；

• 知乎：李锐博恩，右下角二维码。
  

• FPGA/IC技术交流2020