视觉SLAM之鱼眼相机模型

最近研究了视觉SLAM中不同的鱼眼相机模型，其中包括：

Scaramuzza的鱼眼相机模型

代表性的SLAM工作为MultiCo-SLAM,是一个以ORB-SLAM为基础的扩展的多鱼眼相机视觉SLAM系统（Video，Paper）
相机模型论文：A Flexible Technique for Accurate Omnidirectional Camera Calibration and
Structure from Motion
2017年Urban等人在此基础上，投影函数，使结果更加精确，论文地址

Scaramuzza相机模型标定工具：Tools:，其操作流程均可在相应网页中找到。

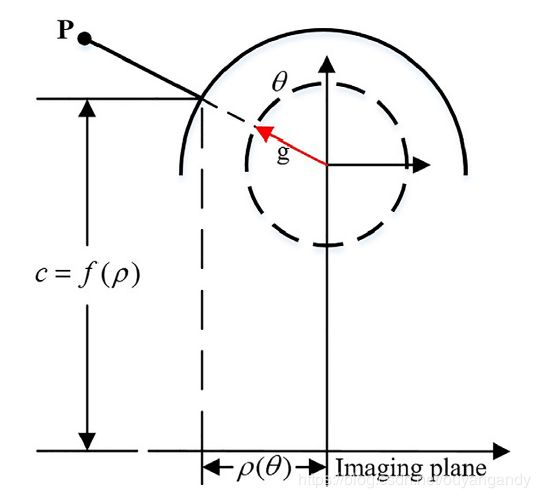
如上图所示，为Scaramuzza模型投影过程。
投影公式：

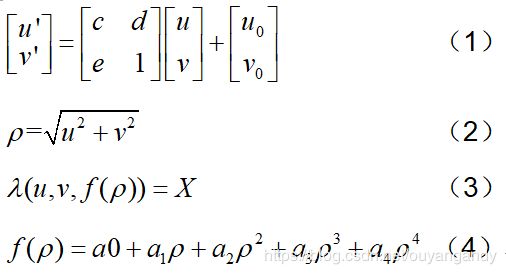
上述公式（1）中，${\left[u^{\prime },v^{\prime }\right]}^T$为image plane，$[u,v{]}^T$为sensor plane，对应于针孔相机模型来说，其实就是像素平面和图像平面。
上述公式（2）中，ρ为到图像中心的径向欧氏距离。
上述公式（3）中，为image point到空间三维点的映射方程。经过标定你会发现a1=0，这是因为，通过观察上图投影模型你会发现，当$f(\rho )$取极大值时，图像坐标x=y=0,也就是入射角为0度，$f(\rho )$取导数，$f^{\prime }(\rho )$=0, $\rho =\sqrt{u^2+v^2}$=0，那么a1=0。
上述公式（4）为投影函数，其实在标定的过程中，主要标定的就是f函数的系数。
用一个示例程序说明Scaramuzza相机模型的投影过程.首先进行标定，下面代码中已经给出标定结果，直接拿来取用，3D点采用随机数产生。部分注释已经写在代码中，欢迎共同交流学习。

// cam_model_general.h
#pragma once

#ifndef CAM_MODEL_GENERAL_H
#define CAM_MODEL_GENERAL_H

#include 

// horner scheme for evaluating polynomials at a value x
template<typename T>
T horner(T* coeffs, int s, T x)
{
	T res = 0.0;
	for (int i = s - 1; i >= 0; i--)
		res = res * x + coeffs[i];

	return res;
}

// template class implementation of the general atan model
template <typename T>
class cCamModelGeneral
{
public:
	// construtors
	cCamModelGeneral() :
		c(T(1)),
		d(T(0)),
		e(T(0)),
		u0(T(0)),
		v0(T(0)),
		p((cv::Mat_<T>(1, 1) << T(1))),
		invP((cv::Mat_<T>(1, 1) << T(1))),
		p_deg(1),
		invP_deg(1),
		Iwidth(T(0)), Iheight(T(0))
	{}

	cCamModelGeneral(cv::Vec<T, 5> cdeu0v0,
		cv::Mat_<T> p_,
		cv::Mat_<T> invP_) :
		c(cdeu0v0[0]),
		d(cdeu0v0[1]),
		e(cdeu0v0[2]),
		u0(cdeu0v0[3]),
		v0(cdeu0v0[4]),
		p(p_),
		invP(invP_)
	{
		// initialize degree of polynomials
		p_deg = (p_.rows > 1) ? p_.rows : p_deg = p_.cols;
		invP_deg = (p_.rows > 1) ? invP_deg = invP_.rows : invP_deg = invP_.cols;

		cde1 = (cv::Mat_<T>(2, 2) << c, d, e, T(1));
	}

	cCamModelGeneral(cv::Vec<T, 5> cdeu0v0,
		cv::Mat_<T> p_,
		cv::Mat_<T> invP_,
		int Iw_, int Ih_) :
		c(cdeu0v0[0]),
		d(cdeu0v0[1]),
		e(cdeu0v0[2]),
		u0(cdeu0v0[3]),
		v0(cdeu0v0[4]),
		p(p_),
		invP(invP_),
		Iwidth(Iw_),
		Iheight(Ih_)
	{
		// initialize degree of polynomials
		p_deg = (p_.rows > 1) ? p_.rows : p_deg = p_.cols;
		invP_deg = (p_.rows > 1) ? invP_deg = invP_.rows : invP_deg = invP_.cols;

		cde1 = (cv::Mat_<T>(2, 2) << c, d, e, T(1));
	}

	~cCamModelGeneral() {}


	template <typename T> inline void
		WorldToImg(const T& x, const T& y, const T& z,    // 3D scene point
			T& u, T& v)					  // 2D image point
	{
		T norm = sqrt(x*x + y*y);
		if (norm == T(0))
			norm = 1e-14;

		T theta = atan(-z / norm);
		T rho = horner<T>((T*)invP.data, invP_deg, theta);

		T uu = x / norm * rho;
		T vv = y / norm * rho;

		u = uu*c + vv*d + u0;
		v = uu*e + vv + v0;

	}

	template <typename T> inline void
		WorldToImg(const cv::Point3_<T>& X,			// 3D scene point
			cv::Point_<T>& m)			// 2D image point
	{
		T norm = sqrt(X.x*X.x + X.y*X.y);

		if (norm == T(0))
			norm = 1e-14;

		T theta = atan(-X.z / norm);

		T rho = horner<T>((T*)invP.data, invP_deg, theta);

		T uu = X.x / norm * rho;
		T vv = X.y / norm * rho;

		m.x = uu*c + vv*d + u0;
		m.y = uu*e + vv + v0;
	}

	// fastest by about factor 2
	template <typename T> inline void
		WorldToImg(const cv::Vec<T, 3>& X,			// 3D scene point
			cv::Vec<T, 2>& m)			// 2D image point
	{

		double norm = cv::sqrt(X(0)*X(0) + X(1)*X(1));

		if (norm == 0.0)
			norm = 1e-14;

		double theta = atan(-X(2) / norm);

		double rho = horner<T>((T*)invP.data, invP_deg, theta);

		double uu = X(0) / norm * rho;
		double vv = X(1) / norm * rho;

		m(0) = uu*c + vv*d + u0;
		m(1) = uu*e + vv + v0;
	}

	template <typename T> inline void
		ImgToWorld(T& x, T& y, T& z,				// 3D scene point
			const T& u, const T& v) 			    // 2D image point
	{
		T invAff = c - d*e;
		T u_t = u - u0;
		T v_t = v - v0;
		// inverse affine matrix image to sensor plane conversion
		x = (1 * u_t - d * v_t) / invAff;
		y = (-e * u_t + c * v_t) / invAff;
		T X2 = x*x;
		T Y2 = y*y;
		z = -horner<T>((T*)p.data, p_deg, sqrt(X2 + Y2));

		// normalize vectors spherically
		T norm = sqrt(X2 + Y2 + z*z);
		x /= norm;
		y /= norm;
		z /= norm;
	}

	template <typename T> inline void
		ImgToWorld(cv::Point3_<T>& X,						// 3D scene point
			const cv::Point_<T>& m) 			            // 2D image point
	{
		T invAff = c - d*e;
		T u_t = m.x - u0;
		T v_t = m.y - v0;
		// inverse affine matrix image to sensor plane conversion
		X.x = (1 * u_t - d * v_t) / invAff;
		X.y = (-e * u_t + c * v_t) / invAff;
		T X2 = X.x*X.x;
		T Y2 = X.y*X.y;
		X.z = -horner<T>((T*)p.data, p_deg, sqrt(X2 + Y2));

		// normalize vectors spherically
		T norm = sqrt(X2 + Y2 + X.z*X.z);
		X.x /= norm;
		X.y /= norm;
		X.z /= norm;
	}

	template <typename T> inline void
		ImgToWorld(cv::Vec<T, 3>& X,						// 3D scene point
			const cv::Vec<T, 2>& m) 			            // 2D image point
	{
		T invAff = c - d*e;
		T u_t = m(0) - u0;
		T v_t = m(1) - v0;
		// inverse affine matrix image to sensor plane conversion
		X(0) = (1 * u_t - d * v_t) / invAff;
		X(1) = (-e * u_t + c * v_t) / invAff;
		T X2 = X(0)*X(0);
		T Y2 = X(1)*X(1);
		X(2) = -horner<T>((T*)p.data, p_deg, sqrt(X2 + Y2));

		// normalize vectors spherically
		T norm = sqrt(X2 + Y2 + X(2)*X(2));
		X(0) /= norm;
		X(1) /= norm;
		X(2) /= norm;
	}

	// get functions
	T Get_c() { return c; }
	T Get_d() { return d; }
	T Get_e() { return e; }

	T Get_u0() { return u0; }
	T Get_v0() { return v0; }

	int GetInvDeg() { return invP_deg; }
	int GetPolDeg() { return p_deg; }

	cv::Mat_<T> Get_invP() { return invP; }
	cv::Mat_<T> Get_P() { return p; }

	T GetWidth() { return Iwidth; }
	T GetHeight() { return Iheight; }

	cv::Mat GetMirrorMask(int pyrL) { return mirrorMasks[pyrL]; }
	void SetMirrorMasks(std::vector<cv::Mat> mirrorMasks_) { mirrorMasks = mirrorMasks_; }

	bool isPointInMirrorMask(const T& u, const T& v, int pyr)
	{
		int ur = cvRound(u);
		int vr = cvRound(v);
		// check image bounds
		if (ur >= mirrorMasks[pyr].cols || ur <= 0 ||
			vr >= mirrorMasks[pyr].rows || vr <= 0)
			return false;
		// check mirror
		if (mirrorMasks[pyr].at<uchar>(vr, ur) > 0)
			return true;
		else return false;
	}

private:
	// affin parameters
	T c;
	T d;
	T e;
	cv::Mat_<T> cde1;
	// principal point
	T u0;
	T v0;
	// polynomial
	cv::Mat_<T> p;
	int p_deg;
	// inverse polynomial
	cv::Mat_<T> invP;
	int invP_deg;
	// image width and height
	int Iwidth;
	int Iheight;
	// mirror mask on pyramid levels
	std::vector<cv::Mat> mirrorMasks;
};


#endif

// cam_model_general.cpp
#include 
#include 

#include "cam_model_general.h"

using namespace std;
using namespace cv;

double time2double(std::chrono::steady_clock::time_point start,
	std::chrono::steady_clock::time_point end)
{
	return static_cast<double>(
		std::chrono::duration_cast<std::chrono::nanoseconds>(end - start).count() * (double)1e-9);
}

double dRand(double fMin, double fMax)
{
	return fMin + (double)rand() / RAND_MAX * (fMax - fMin);
}

int main()
{
	// number of iterations for speed test
	long iterations = 1e8;

	// take some real world cam model
	// this is the camera model of data set Fisheye1_
	// ATTENTION!! I also switched the principal point coordinates
	Vec<double, 5> interior_orientation(0.998883018922937, -0.0115128845387445,	//cdeu0v0 均是标定得到
		0.0107836324042904, 544.763473297893, 378.781825009886);
	Mat_<double> p = (Mat_<double>(5, 1) << -338.405137634369,  // poly系数，标定得到
		0.0,
		0.00120189826837736,
		-1.27438189154991e-06,
		2.85466623521256e-09);
	// attention: this is the reverse order of findinvpoly 
	// as matlab evaluates the polynomials differently
	Mat_<double> pInv = (Mat_<double>(11, 1) << 510.979186217526, // invPoly系数，标定得到
		291.393724562448,
		-13.8758863124724,
		42.4238251854176,
		23.054291112414,
		-7.18539785128328,
		14.1452111052043,
		18.5034196957122,
		-2.39675686593404,
		-7.18896323060144,
		-1.85081569557094);

	// here comes the camera model
	cCamModelGeneral<double> camModel(interior_orientation, p, pInv);

	// test the correctness of the implementation, at least internally
	double x0 = dRand(0, 5);//不应该是随机数产生的3D点么？为什么每次运行都一样呢？
	double y0 = dRand(0, 5);
	double z0 = dRand(0, 5);

	Vec3d vec3d(x0, y0, z0);
	Vec3d vec3d_normalized = (1 / norm(vec3d)) * vec3d;
	Vec2d projection;
	Vec3d unprojected;
	camModel.WorldToImg(vec3d, projection);//3D点投影到2D点
	cout << "projected point: " << projection << endl;

	camModel.ImgToWorld(unprojected, projection);//把2D点投影到3D点，但这个3D点是归一化的三维点
	cout << "unprojected:" << unprojected << endl;
	cerr << "difference after unproject: " << norm(vec3d_normalized - unprojected) << endl;

	std::chrono::steady_clock::time_point begin = std::chrono::steady_clock::now();
	// timings
	for (int i = 0; i < iterations; ++i)
	{
		camModel.WorldToImg(vec3d, projection);
		camModel.ImgToWorld(unprojected, projection);
	}
	std::chrono::steady_clock::time_point end = std::chrono::steady_clock::now();
	cout << "total time for " << iterations << " iterations of world2cam and cam2world: " << time2double(begin, end) << " s" << endl;
	cout << "time for one iteration: " << time2double(begin, end) / iterations * 1e9 << " nano seconds" << endl;
	return 0;
}

mei相机模型

数学模型如下所示。也是VINS-mono所用的相机模型。具体可参考网页
相机模型的参考论文

未完待续~~仿佛说的不够细致，仿佛什么都没说。